Clausius-Clapeyron Equation
- Page ID
- 11877
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Apply the Clausius-Clapeyron equation to estimate the vapor pressure at any temperature.
- Estimate the heat of phase transition from the vapor pressures measured at two temperatures.
The vaporization curves of most liquids have similar shapes with the vapor pressure steadily increasing as the temperature increases (Figure \(\PageIndex{1}\)).
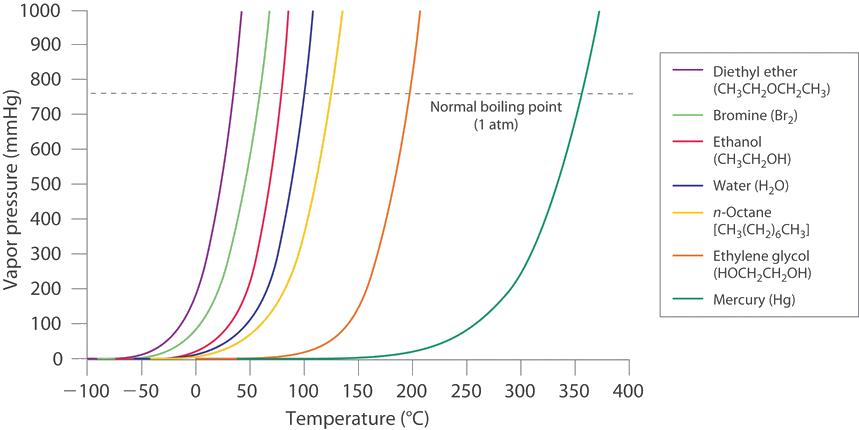
A good approach is to find a mathematical model for the pressure increase as a function of temperature. Experiments showed that the vapor pressure \(P\) and temperature \(T\) are related,
\[P \propto \exp \left(- \dfrac{\Delta H_{vap}}{RT}\right) \ \label{1}\]
where \(\Delta{H_{vap}}\) is the Enthalpy (heat) of Vaporization and \(R\) is the gas constant (8.3145 J mol-1 K-1).
A simple relationship can be found by integrating Equation \ref{1} between two pressure-temperature endpoints:
\[\ln \left( \dfrac{P_1}{P_2} \right) = \dfrac{\Delta H_{vap}}{R} \left( \dfrac{1}{T_2}- \dfrac{1}{T_1} \right) \label{2}\]
where \(P_1\) and \(P_2\) are the vapor pressures at two temperatures \(T_1\) and \(T_2\). Equation \ref{2} is known as the Clausius-Clapeyron Equation and allows us to estimate the vapor pressure at another temperature, if the vapor pressure is known at some temperature, and if the enthalpy of vaporization is known.
The order of the temperatures in Equation \ref{2} matters as the Clausius-Clapeyron Equation is sometimes written with a negative sign (and switched order of temperatures):
\[\ln \left( \dfrac{P_1}{P_2} \right) = - \dfrac{\Delta H_{vap}}{R} \left( \dfrac{1}{T_1}- \dfrac{1}{T_2} \right) \label{2B} \]
The vapor pressure of water is 1.0 atm at 373 K, and the enthalpy of vaporization is 40.7 kJ mol-1. Estimate the vapor pressure at temperature 363 and 383 K respectively.
Solution
Using the Clausius-Clapeyron equation (Equation \(\ref{2B}\)), we have:
\[\begin{align} P_{363} &= 1.0 \exp \left[- \left(\dfrac{40,700}{8.3145}\right) \left(\dfrac{1}{363\;K} -\dfrac{1}{373\; K}\right) \right] \nonumber \\[4pt] &= 0.697\; \text{atm} \nonumber \end{align} \nonumber\]
\[\begin{align} P_{383} &= 1.0 \exp \left[- \left( \dfrac{40,700}{8.3145} \right)\left(\dfrac{1}{383\;K} - \dfrac{1}{373\;K} \right) \right] \nonumber \\[4pt] &= 1.409\; \text{atm} \nonumber \end{align} \nonumber\]
Note that the increase in vapor pressure from 363 K to 373 K is 0.303 atm, but the increase from 373 to 383 K is 0.409 atm. The increase in vapor pressure is not a linear process.
Discussion
We can use the Clausius-Clapeyron equation to construct the entire vaporization curve. There is a deviation from experimental value, that is because the enthalpy of vaporization varies slightly with temperature.
The Clausius-Clapeyron equation can be also applied to sublimation; the following example shows its application in estimating the heat of sublimation.
The vapor pressures of ice at 268 K and 273 K are 2.965 and 4.560 torr respectively. Estimate the heat of sublimation of ice.
Solution
The enthalpy of sublimation is \(\Delta{H}_{sub}\). Use a piece of paper and derive the Clausius-Clapeyron equation so that you can get the form:
\[\begin{align*} \Delta H_{sub} &= \dfrac{ R \ln \left(\dfrac{P_{273}}{P_{268}}\right)}{\dfrac{1}{268 \;K} - \dfrac{1}{273\;K}} \\[4pt] &= \dfrac{8.3145 \ln \left(\dfrac{4.560}{2.965} \right)}{ \dfrac{1}{268\;\text{K}} - \dfrac{1}{273\;\text{K}} } \\[4pt] &= 52,370\; \text{J mol}^{-1}\nonumber \end{align*}\]
Note that the heat of sublimation is the sum of heat of melting (6,006 J/mol at 0°C and 101 kPa) and the heat of vaporization (45,051 J/mol at 0 °C).
Show that the vapor pressure of ice at 274 K is higher than that of water at the same temperature. Note the curve of vaporization is also called the curve of vaporization.
Calculate \(\Delta{H_{vap}}\) for ethanol, given vapor pressure at 40 oC = 150 torr. The normal boiling point for ethanol is 78 oC.
Solution
Recognize that we have TWO sets of \((P,T)\) data:
- Set 1: (150 torr at 40+273K)
- Set 2: (760 torr at 78+273K)
We then directly use these data in Equation \ref{2B}
\[\begin{align*} \ln \left(\dfrac{150}{760} \right) &= \dfrac{-\Delta{H_{vap}}}{8.314} \left[ \dfrac{1}{313} - \dfrac{1}{351}\right] \\[4pt] \ln 150 -\ln 760 &= \dfrac{-\Delta{H_{vap}}}{8.314} \left[ \dfrac{1}{313} - \dfrac{1}{351}\right] \\[4pt] -1.623 &= \dfrac{-\Delta{H_{vap}}}{8.314} \left[ 0.0032 - 0.0028 \right] \end{align*}\]
Then solving for \(\Delta{H_{vap}}\)
\[\begin{align*} \Delta{H_{vap}} &= 3.90 \times 10^4 \text{ J/mol} \\[4pt] &= 39.0 \text{ kJ/mol} \end{align*} \]
It is important to not use the Clausius-Clapeyron equation for the solid to liquid transition. That requires the use of the more general Clapeyron equation
\[\dfrac{dP}{dT} = \dfrac{\Delta \bar{H}}{T \Delta \bar{V}} \nonumber\]
where \(\Delta \bar{H}\) and \(\Delta \bar{V}\) is the molar change in enthalpy (the enthalpy of fusion in this case) and volume respectively between the two phases in the transition.

