13.4: Pressure and Temperature Effects on Solubility
- Page ID
- 44040
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
In this section we will look at how the pressure and temperature effect solubility.
When we look at pressure effects, we are considering the pressure of a gas over a liquid, and so the solute is necessarily a gas, and we will introduce Henry's law to describe this.
When we look at the temperature effect, the solute can be a solid or a gas, and the temperature effects can often be very different. We will introduce solubility curves to describe the temperature effects, noting that gas solubilities go down as temperature goes up, but solid solubilities usually, but not always increase upon heating.
Pressure Effects on Solubility
When a gas phase molecule hits the surface of a liquid it may be deflected back into the gas or dissolved into the solution, in the latter case becoming a solute particle. If a dissolved molecule reaches the surface of the liquid, a fraction will have enough kinetic energy to escape, and so particles are being exchanged across the liquid/gas boundary all the time. When the rate at which the gas phase particles enter and leave are equal you have a dynamic equilibrium, where the concentration in each phase becomes a constant value. The solubility is a measure of the concentration of the dissolved gas particles in the liquid and is a function of the gas pressure. As you increase the pressure of a gas, the collision frequency increases and thus the solubility goes up, as you decrease the pressure, the solubility goes down..
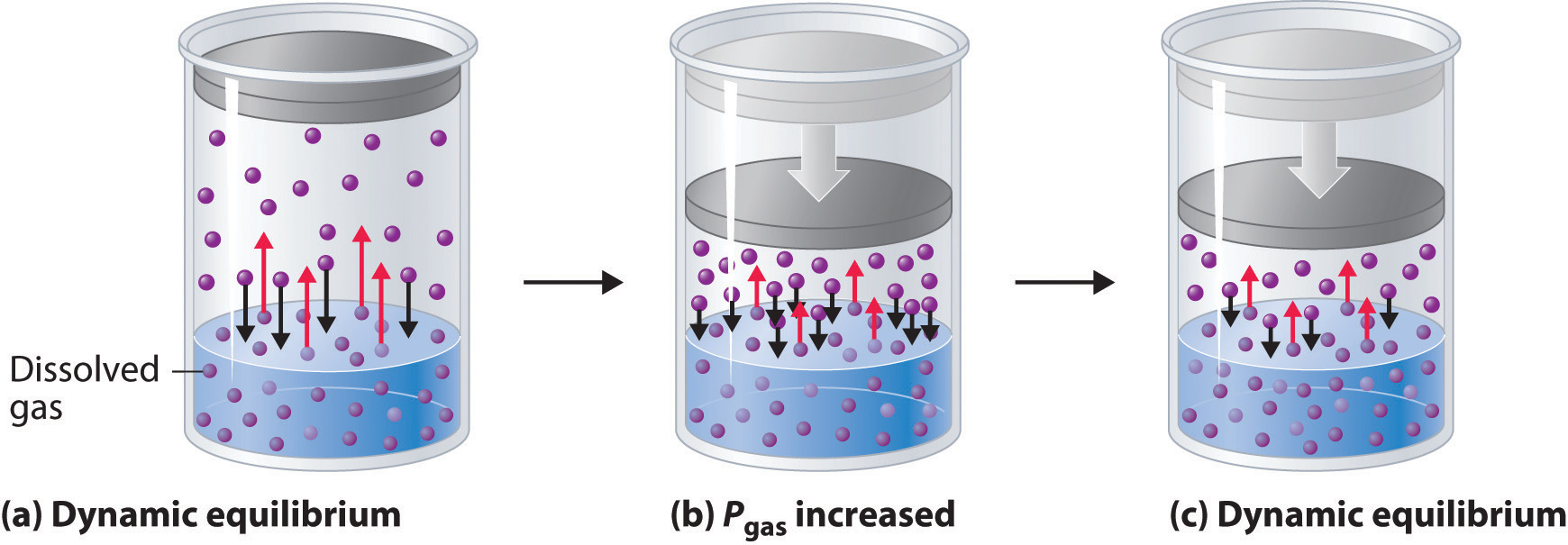
Figure \(\PageIndex{1}\): This figure shows how the solubility of a gas can be understood as a dynamic process where gaseous particles are transitioning across the boundary between the two phases.
Figure 13.3.1 shows a system at equilibrium (a) where the rate across the suface/vapor boundary is constant (red arrows equal black arrows). In (b) the pressure is increased (by decreasing the volume). This increases the concentration in the vapor phase, and so the collision frequency with the liquid increases, causing more to be dissolved. As the concentration in the liquid increases the rate of escape equals, and the concentration rises until the rate of escape equals the rate at which they are entering the liquid, when a new equilbrium occurs (c).
Exercise \(\PageIndex{1}\)
What would be the effect if the gas in figure 13.3.1 was reduced in pressure?
- Answer
-
The solubility would decrease because there would be less molecules hitting the surface.
The relationship between the solubility of a gas and its pressure is a linear one, and can be described by Henry's law.
Video \(\PageIndex{1}\): 0:27 professional animation uploaded by kwesiamoa showing how the solubility of a gas is a function of pressure
Henry's Law
Henry's law states that the concentration of a gaseous solute in a liquid is proportional to the absolute pressure. This explains commonly observed phenomena like the degassing of a can of carbonated beverage upon opening. While sealed, there was no room for gas to expand and so the pressure would be high, resulting in a high dissolved concentration. This system was at equilibrium, but once it was opened, the gas pressure dropped and created a state of disequilibrium, with the gas leaving the fluid far mor rapidly than it was entering. Overtime, the system reached a new equilibrium, and the carbonated beverage became "flat".
Henry's Law Constant
\[\underbrace{C=kP}_{\text{ Henry's Law }}\]
In the above equation, C= concentration, k= Henry's Law constant and P is the partial pressure of the gas that dissolves. Henry's law describes the solubility of a specific gas in a specific solvent and is a strong function of the temperature. So a table of Henry's law constants for various gasses must define the solvent and the temperature for which they apply, and care must be taken that these are the same when comparing constants from different sources. The point is that there is no such thing as Henry's law constant for carbon dioxide, there is one for carbon dioxide at 25oC in water, another in ethanol and another in benzene...
It should be noted that there are many units for concentration and so "C" may mean different things (Molality, Molarity, ppm,...), and of course there are many units for pressure (atm, torr, bar,...), which students often find this confusing. Probably the best way to write out Henry's law is to look at the units of the constant. So for:
k(CO2) in water at 20oC = 0.034 \(\frac{mol}{kg\cdot bar}\), I would use, m=kP, where m=molality,
for
k(CO2) in water at 25oC = 3.92x10-2 \(\frac{mol}{L\cdot atm}\), I would use M=kP, where M=molarity.
(The important thing is to always look at the units of k)
Exercise \(\PageIndex{1}\)
What is Henry's Law constant if the solubility of oxygen is 40mg/L water at 1 bar. Express in the given units, and convert to \(\frac{mol}{L\cdot atm}\)
- Answer
-
\(C=kP\; k=\frac{C}{P}\;=\frac{40mg\, O_{2}}{L\cdot bar}\).
To convert to \(\frac{mol}{L\cdot atm}\):
\(\frac{40mg\, O_{2}}{L\cdot bar}\left ( \frac{g\, O_{2}}{10^{3}\, mg\, O_{2}} \right )\left ( \frac{molO_{2}}{32g} \right )\left ( \frac{bar}{0.987atm} \right )=1.27x10^{-3}\frac{mol}{l\cdot atm}\)
Two State Approach
Even without knowing Henry's Law constant, if you know the solubility at one pressure, you can determine it at another.
\[C_1=kP_1 \\ \; \\ \text{dividing both sides by the concentration at a different pressure} \\ \; \\\frac{C_{1}}{C_{2}}=\frac{kP_{1}}{C_{2}} \\ \; \\ substituting \;\; C_2=kP_2 \\ \; \\ \frac{C_{1}}{C_{2}}=\frac{\cancel{k}P_{1}}{\cancel{k}P_{2}}=\frac{P_{1}}{P_{2}}\\ C_{2}=C_{1}\frac{P_{2}}{P_{1}}\]
Where the subscripts 1 indicates the concentration at one pressure and the subscript 2 indicates the concentration at a different pressure
Exercise \(\PageIndex{2}\)
If the solubility of carbon dioxide is 1.45g/L at 25oC and 100 kPa, what is it at 50 kPa? And give answer in units of Molarity.
- Answer
-
Ok, if you think about it, you halved the pressure, so you are going to halve the concentration and it will be 0.725g/L. This is the same as asking what is the volume of 10 grams of a solid of constant density if 20 grams is 10mL. We simply take the two state approach for Henry's Law.
\[\frac{C_{1}}{C_{2}}=\frac{kP_{1}}{kP_{2}}=\frac{P_{1}}{P_{2}}\\ C_{2}=C_{1}\frac{P_{2}}{P_{1}}\\ =1.45(\frac{g}{L})\frac{50kPa}{100kPa}\\ =0.725\frac{g}{L} \nonumber\]
In units of molarity
\[M=0.725\frac{g}{L} \left ( \frac{molCO_{2}}{44.01g} \right )=0.0165M \; CO_{2} \nonumber\]
or 16.5mM CO2
Temperature Effect on Solubility
The temperature effect depends on the nature of the solute and the solvent, and their interactions. These are completely different between solid solutes and gaseous ones. The propensity of a solid is to become more soluble as temperature goes up, and for a gas to become less soluble. We will revisit this in chapter 18 when we cover entropy and the second law of thermodynamics, which essentially says that a process goes in the direction that increases the entropy of the universe, that is, how dispersed the universe is. Spontaneous process tend to occur when reactions are exothermic and particles become more dispersed, but sometimes solvation can get real tricky, as dissolving an ion can induce order in the solvent, as when ion-dipole interactions cause the polar molecules to align around the ions. The "Rule of Thumb" is that with increasing temperature gas solubility goes down and solid solubility goes up, but there are cases where the later is not true.
Temperature and Gas Phase Solubility
In chapter 11 we saw that increasing the temperature increased the vapor pressure above the surface of a pure volatile liquid. This was because more molecules had enough kinetic energy to escape the liquid and enter the vapor phase (figure 11.6.5) . In that chapter we were talking about a pure substance, but if a solution with a gas dissolved in it is heated, it too gains kinetic energy, increases the fraction of collisions at the surface that have enough energy to escape the surfaces forces of the solution, and so the concentration of those remaining dissolved goes down. Figure 13.3.2 shows how the solubility of a gas in water goes down as the temperature is raised. This decrease in the solubility of oxygen as temperature goes up is one of the reasons cold water fish like trout can not live in warm water.
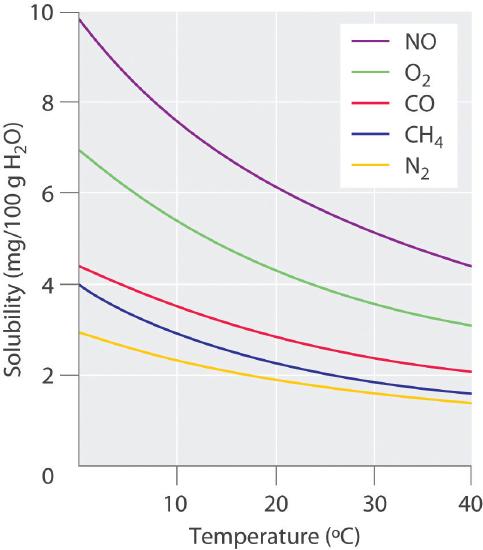
Figure \(\PageIndex{2}\): Solubility of several gasses in water
Temperature and Solid Phase Solubility
Figure 13.3.3 shows the solubility of many ionic and covalent compounds in water. There are a wide range of dependencies on the temperature and although most compounds increase their solubility as heated, some actually show a decrease. We will revisit this material when we get to chapter 18 and cover entropy and Gibb's free energy.
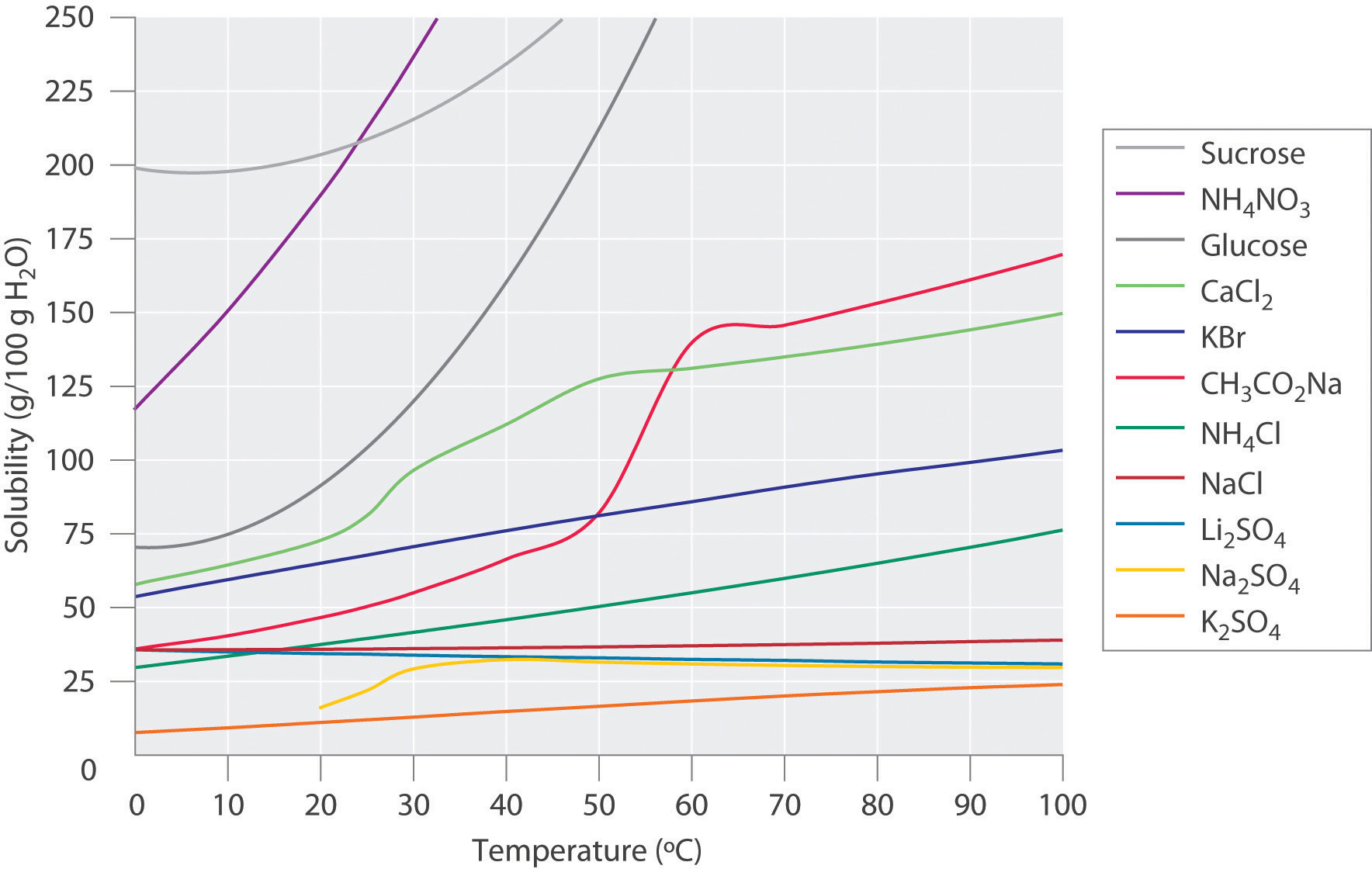
Figure \(\PageIndex{3}\): Solubility of various covalent and ionic solids in water
Some of the molecules in the gas phase condense when they contact the liquid and some in the liquid evaporate into the gas. Thus the molecules can be considered to be partioned across both phases, with some in the liquid and some in the gas phase. For a system at equilibrium the rate they enter the gas phase equals the rate at which they enter the liquid, and so the concentration in both phases is constant.
In Class Activity
ADAPT \(\PageIndex{1}\)
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:


