13.3: Solvation Processes
- Page ID
- 44039
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Solvation, or dissolution, is the process by which a solute dissolves into a solvent.
As indicated in figure 13.2.1, solvation can be considered to occur in three steps.
- Step 1: Separate particles of the solute from each other
- Step 2: Separate particles of the solvent from each other
- Step 3: Combine separated solute and solvent particles to make solution
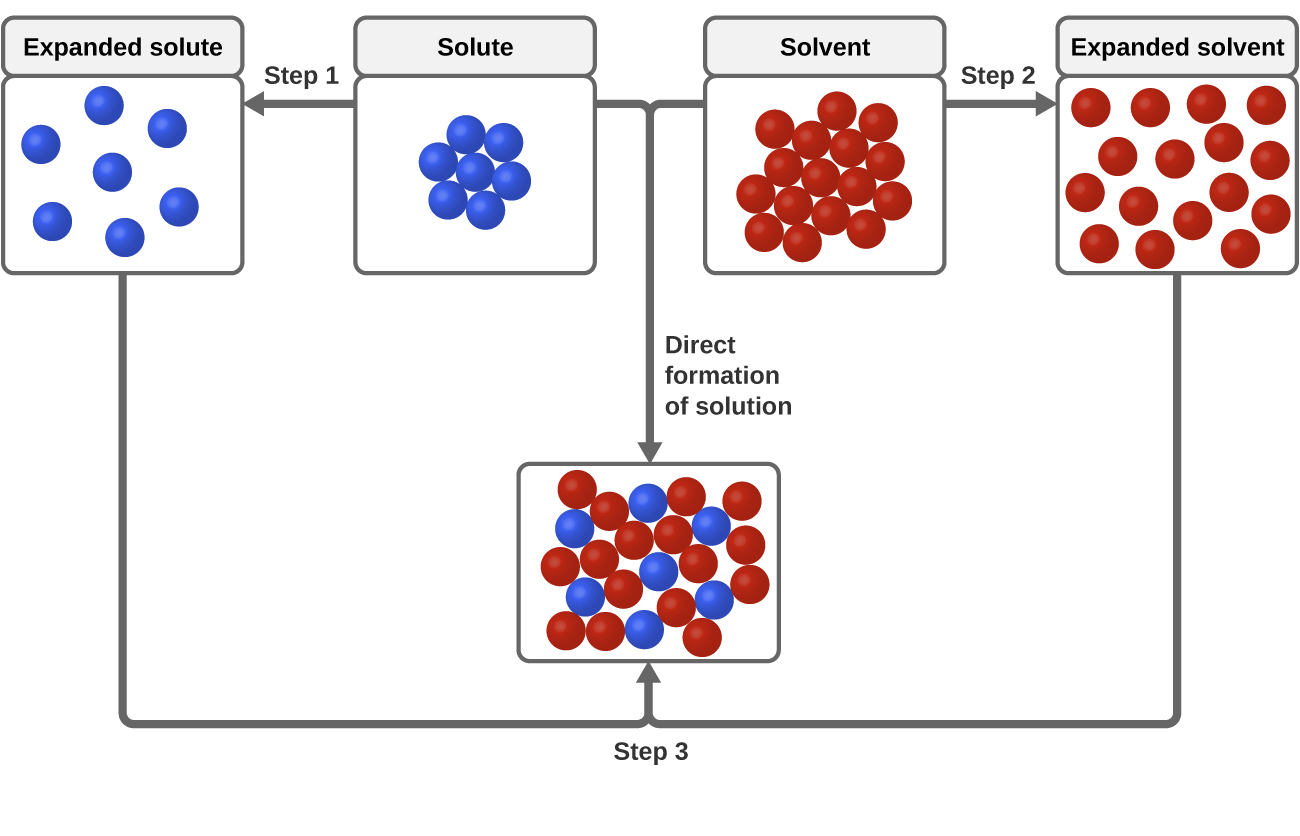
Figure \(\PageIndex{1}\): Visualization of solvation process as taking place in 3 distinct steps.
Note, in the above diagram the first two steps require breaking apart the pure solute and the pure solvent, while the second requires forming the solution.
Energetics of Dissolution
Enthalpy is a state function and thus path independent. So the energetics requires breaking apart the solute (step 1) and the solvent (step 2) and then forming the solution (step 3).
- Step 1: Separate particles of the solute from each other [ENDOTHERMIC]
- Step 2: Separate particles of the solvent from each other [ENDOTHERMIC]
- Step 3: Combine separated solute and solvent particles to make solution [EXOTHERMIC]
Exercise \(\PageIndex{1}\)
Why are the first two steps endothermic, but the third exothermic?
- Answer
-
The first law of thermodynamics states that the energy of the universe is conserved, that the universe can be partitioned between a system and the surroundings, and that positive energy is energy added to the system (endothermic) and "negative energy" is energy added to the surroundings (exothermic), which is lost by the system. By "negative energy" we do not mean that energy is negative, but that the flow of energy is from the system to the surroundings and thus the system loses energy. It may be better to say the "flow of energy", but we often associate energy with a reaction, that is the change of energy of the system during a reaction, and that may be positive or negative, depending on if it is endothermic or exothermic. So lets look at energy from the perspective of the energy associated with each step of the the process.
Since you add energy to break apart something (intermolecular forces in the case of a solute and intramolecular forces in the case of the solvent), the first two steps are endothermic.
The third step is exothermic, which may be easier understood by looking at the opposite process. That is, to break a solution apart into its separate components must require energy, and since energy is conserved, the opposite process, that of forming the solution from its separated pieces must release that energy, and so it is exothermic.
So when is dissolution endothermic and when is it exothermic? From figure 13.1.1 we can see that the direct process is the summation of the three steps. If the endothermic steps (1 & 2) are larger than the exothermic step (2), it is endothermic. If they are less, it is exothermic.
Exothermic Solvation Processes
This is illustrated in the energy cycle of figure 13.2.2. Since enthalpy is a state function the energy going from solvent and solute to solution is independent of the path, and there are two paths, the direct route, represented in green as \(\Delta\)Hsoln and that of steps 1,2,3. So
\[\Delta H_{soln} = \Delta H_1 + \Delta H_2 + \Delta H_3.\]
Since \(\Delta H_3\) releases more energy than \(\Delta H_1 + \Delta H_2\) absorb, the process is exothermic, and
\[\Delta H_{soln} <0\]
Figure \(\PageIndex{2}\): An exothermic solvation process where the exothermic step releases more energy than the endothermic steps absorb. Such a process will heat the surroundings.
Endothermic Solvation Processes
This is illustrated in the energy cycle of figure 13.2.3 . Here the two endothermic steps absorb more energy than the exothermic step releases, and so the dissolution process is endothermic.
\(\Delta\)Hsoln = \(\Delta\)H1 + \(\Delta\)H2 + \(\Delta\)H3 . Since \(\Delta\)H1 + \(\Delta\)H2 absorb more energy than \(\Delta\)H3 releases, the overall process is endothermic, and
\(\Delta\)Hsoln > 0
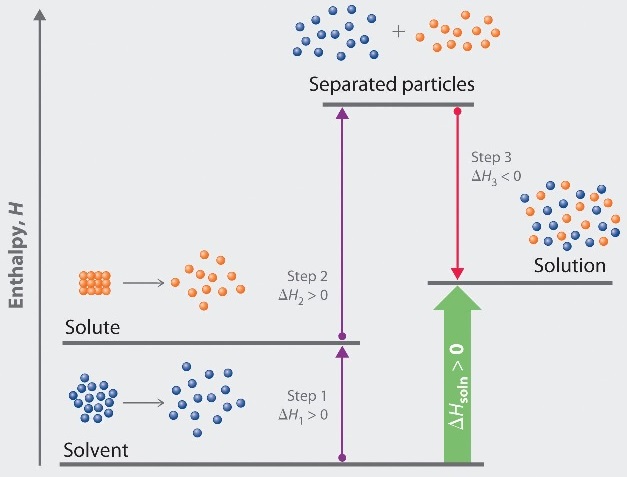
Figure \(\PageIndex{3}\): An endothermic solvation process where the endothermic steps absorb more energy than the exothermic releases. Such a process will cool the surroundings.
Video \(\PageIndex{1}\): 3:48 Minute YouTube by Gydeon Rozen of the Technion Israel Institute of Technology. In the first part they demo the exothermic dissolution of calcium chloride in water, in the second part they demonstrate the endothermic reaction of the dissolution of uera in water.
In Class Activity
ADAPT \(\PageIndex{1}\)


