1.1.2: Effective Nuclear Charge
- Page ID
- 195506
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Effective Nuclear Charge (\(Z_{eff}\))
|
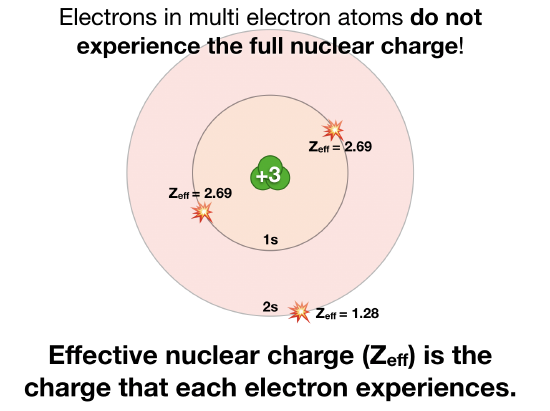
Figure \(\PageIndex{1}\). Effective nuclear charge in a Li atom. (CC-BY-NC-SA; Kathryn Haas) |
The ideal gas law is easy to remember and apply in solving problems, as long as you get the proper values a
According to Coulomb's law, the attraction of an electron to a nucleus depends only on three factors: the charge of the nucleus (+Z), the charge of the electron (-1), and the distance between the two (\(r\)). Coulomb's law works well for predicting the energy of an electron in a hydrogen atom (H has only two particles: one nucleus and one electron). It also works for hydrogen-like atoms: any nucleus with exactly one electron (a He+ ion, for example, has one electron). However, Coulomb's law is insufficient for predicting the energies of electrons in multi-electron atoms and ions.
Electrons within a multi-electron atom interact with the nucleus and with all other electrons. Each electron in a multi-electron atom experiences both attraction to the nucleus and repulsion from interactions with other electrons. The presence of multiple electrons decreases the nuclear attraction to some extent. Each electron in a multi-electron atom experiences a different magnitude of (and attraction to) the nuclear charge depending on what specific subshell the electron occupies. The amount of positive charge experienced by any individual electron is the effective nuclear charge (\(Z_{eff}\)). **
For example, in lithium (Li), none of the three electrons "feel" the full +3 charge from the nucleus (see Cartoon). Rather, each electron "feels" a \(Z_{eff}\) that is less than the actual Z and that depends on the electron's orbital. The actual nuclear charge in Li is +3; the 1s electrons experience a \(Z_{eff}\) =+2.69, and the 2s electron experiences a \(Z_{eff}\) = 1.28. In general, core electrons (or the electrons closest to the nucleus), "feel" a \(Z_{eff}\) that is close to, but less than, the actual nuclear charge (Z). On the other hand, outer valence electrons experience a \(Z_{eff}\) that is much less than Z.
In summary:
- Core electrons: \(Z^* \lessapprox Z\)
- Valence electrons: \(Z^* \ll Z\)
**You will also see \(Z_{eff}\) represented as \(Z^*\): specifically in the section in which you reviewed Periodic Trends, the symbol \(Z^*\) was used.
Slater's rules for estimating \(Z_{eff}\)
|
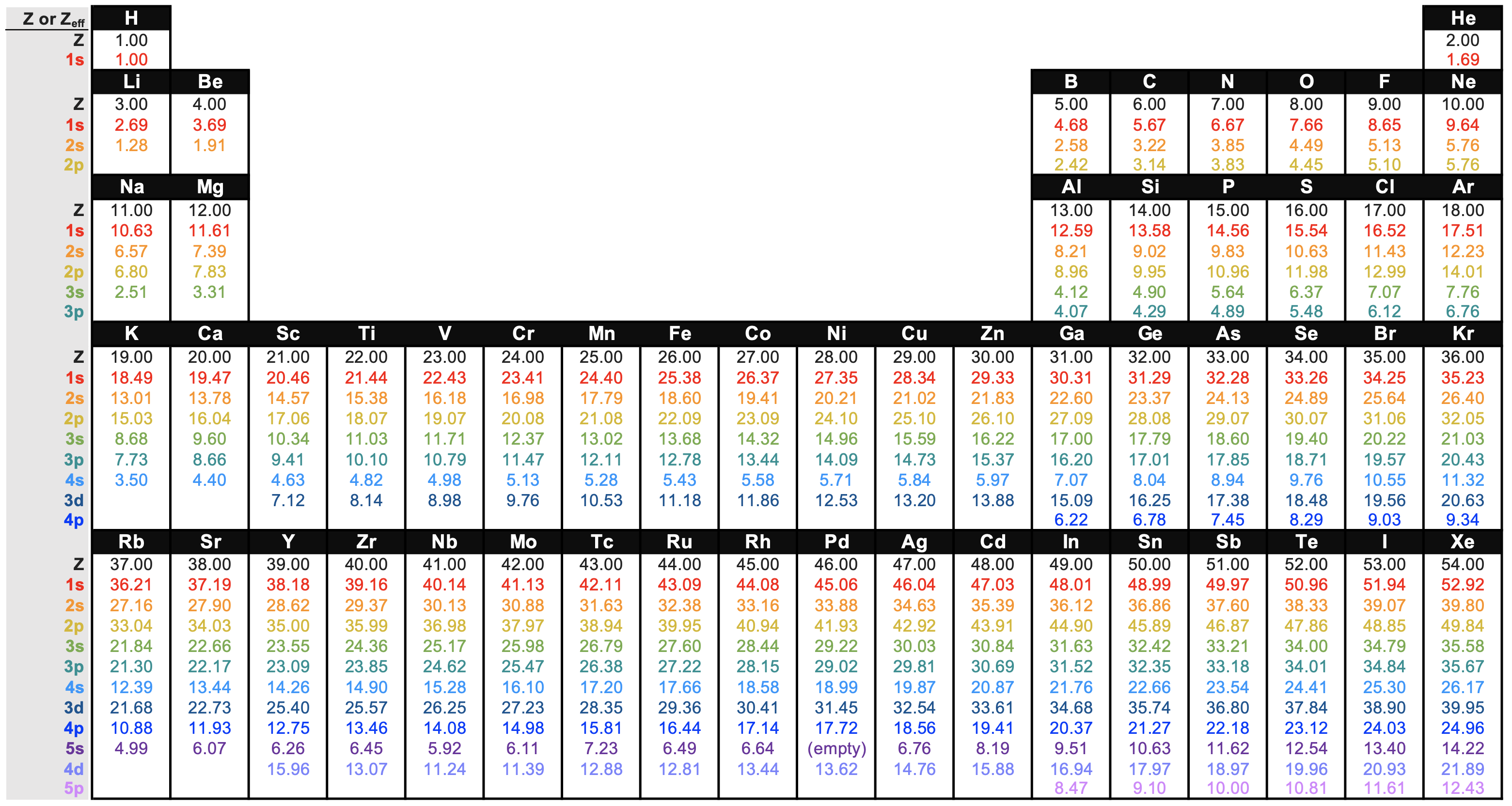
Figure \(\PageIndex{2}\). Diagram illustrating effective nuclear charge according to Slater's rules. |
The \(Z_{eff}\) can be estimated using a number of different methods; probably the best known and most commonly used method is known as Slater's Rules. Slater developed a set of rules to estimate \(Z_{eff}\) depending on how many other electrons exist in the atom and on the orbital location of the electron-of-interest. These two factors are important determinants in shielding (see next section), and they are used to calculate a shielding constant (\(\sigma\)) used in Slater's formula:
\[Z_{eff}=Z-\sigma\]
where Z is the actual nuclear charge (the atomic number) and \(Z_{eff}\) is the effective nuclear charge.
To calculate \(\sigma\), we will write out all the orbitals in an atom, separating them into "groups". Each change in shell number is a new group; s and p subshells are in the same group but d and f orbitals are their own group. You write out all the orbitals using parentheses until you get to the group of the electron-of-interest, like this:
(1s)(2s,2p)(3s,3p)(3d)(4s,4p)(4d)(4f)(5s,5p) etc.
**Critical: The orbitals must be written in order of increasing energy!
- Electrons in the same Group(): Each other electron (not counting the electron-of-interest) in the same group () as the chosen electron, contributes 0.35 to \(\sigma\).
Conceptually, this means electrons in the same group shield each other 35%. - Electrons in Groups() to the left:
- If the electron-of-interest is in a d or f subshell, every electron in groups () to the left contributes 1.00 to \(\sigma\).
Conceptually, this means that d and f electrons are shielded 100% by all electrons in the same shell with a smaller value of \(l\), as well as all electrons in lower shells (\(n\)). - If the electron-of-interest is in an s or p subshell, all electrons in the next lower shell (n - 1) contribute 0.85 to \(\sigma\). And all the electrons in even lower shells contribute 1.00 to \(\sigma\).
Conceptually, this means that s and p electrons are shielded 85% by the electrons one shell lower, and 100% by all electrons in shells n - 2 or lower.
- If the electron-of-interest is in a d or f subshell, every electron in groups () to the left contributes 1.00 to \(\sigma\).
- 1s electrons: \(\sigma\) of a 1s electron is just (\sigma=0.3\), no matter the element.
A video explaining how to use Slater's Rules
What is the \(Z_{eff}\) experienced by the valence electrons in the three isoelectronic species: fluorine anion (F-), neutral neon atom (Ne), and sodium cation (Na+)?
Solution
Each species has 10 electrons, and the number of core electrons is 2 (10 total electrons - 8 valence), but the effective nuclear charge varies because each has a different atomic number (Z). The approximate \(Z_{eff}\) can be found with Slater's Rules. For all of these species, we would calculate the same sigma value:
Calculating \(\sigma\): (1s)(2s,2p), \(\sigma = 2(0.85) + 7(0.35) = 1.7 + 2.45 = 4.15 \)
Fluorine anion: \(Z_{eff}=9-\sigma = 9 - 4.15 = 4.85\)
Neon atom: \(Z_{eff}=10-\sigma = 10 - 4.15 = 5.85\)
Sodium Cation: \(Z_{eff}=11-\sigma = 11 - 4.15 = 6.85\)
So, the sodium cation has the greatest effective nuclear charge.
Calculate Zeff for a 3d-electron in a zinc (Zn) atom.
- Answer
-
Write out the relevant orbitals: (1s)(2s,2p)(3s,3p)(3d)
(4s)Notice that although 4s is fully occupied, we don't include it because in Zn, 4s is higher in energy than 3d, and is thus to the right of the d electrons we are looking at. The electron-of-interest is in 3d, so the other nine electrons in 3d each contribute 0.35 to the value of S. The other 18 electrons each contribute 1 to the value of S.
\(S=18(1)+9(0.35)=21.15\)
\(Z_{eff}=30-21.15=8.85\)
So, although the nuclear charge of Zn is 30, the 3d electrons only experience a \(Z_eff \approx 8.85\)!
"Best" values for \(Z_{eff}\)
Slater's rules are a set of simple rules for predicting \(\sigma\) and \(Z_{eff}\) based on empirical evidence from quantum mechanical calculations. In other words, the \(Z_{eff}\) calculated from Slater's rules are approximate values. The values considered to be the most accurate are derived from quantum mechanical calculations directly. You can find these values in a nice chart on the Wikipedia article of Effective Nuclear Charge. I've recreated the chart in Figure \(\PageIndex{3}\) for convenience:
\(Z_{eff}\) modulates attraction
When valence electrons experience less nuclear charge than core electrons, different electrons experiencing different magnitudes of attraction to the nucleus. A modified form of Coulomb's Law is written below, where \(e\) is the charge of an electron, \(Z_{eff}\) is the effective nuclear charge experienced by that electron, and \(r\) is the radius (distance of the electron from the nucleus).
\[ F_{eff}=k \dfrac{Z_{eff}e^2}{r^2}\]
This formula would suggest that if we can estimate \(Z_{eff}\), then we can predict the attractive force experienced by, and the energy of, an electron in a multi-electron atom, like Li.
The attraction of the nucleus to valence electrons determines the atomic or ionic size, ionization energy, electron affinity, and electronegativity. The stronger the attraction, and the stronger \(Z_{eff}\), the closer the electrons are pulled toward the nucleus. This in turn results in a smaller size, higher ionization energy, higher electron affinity, and stronger electronegativity.
General Periodic Trends in \(Z_{eff}\)
Close inspection of Figure \(\PageIndex{3}\) and analysis of Slater's rules indicate that there are some predictable trends in \(Z_{eff}\). The data from Figure \(\PageIndex{3}\) is plotted below in Figure \(\PageIndex{4}\) to provide a visual aid to the discussion below.
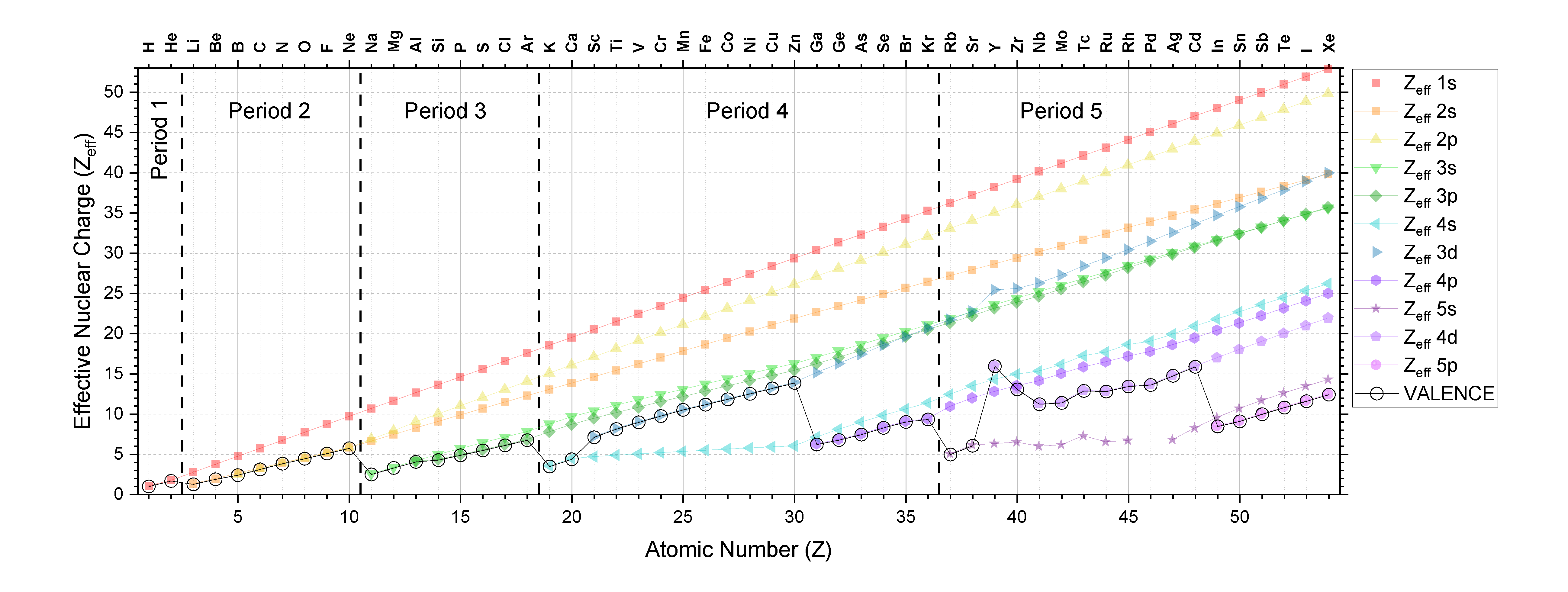
Trends in \(Z_{eff}\) for electrons in a specific shell and subshell
The \(Z_{eff}\) for electrons in a given shell and subshell generally increases as atomic number increases; this trend holds true going across the periodic table and down the periodic table. Convince yourself that this is true for any subshell by examining Figure \(\PageIndex{4}\).
- Do you notice any exceptions to this general trend?
-
Inspection of figure \(\PageIndex{4}\) should confirm for you that the \(Z_{eff}\) increases as Z increases for electrons in any subshell (like the 1s subshell for example, which is plotted above as a red line with square points). You can see this trend as the positive slope in each series. There is one obvious exception in Period 5 in elements 39 (Y) to 41 (Nb; the \(Z_{eff}\) of 4s actually decreases across these three elements as atomic number increases. There is also an exception between Y and Zr in the 3d subshell, and between Tc and Ru in the 5s subshell.
For valence electrons:
It is useful to understand trends in valence \(Z_{eff}\) because the valence \(Z_{eff}\) determines atomic/ionic properties and chemical reactivity. The trends in the valence \(Z_{eff}\) are not simple because as atomic number increases, the valence shell and/or subshell also changes. The valence \(Z_{eff}\) is indicated in Figure \(\PageIndex{4}\) as a black line with open circles.
Down the table: As we go down a column of the periodic table, the valence \(Z_{eff}\) increases. This is a simple trend because type of subshell is consistent and there is an increase only in shell and in atomic number, Z. This trend is best illustrated by inspection of Figure \(\PageIndex{3}\).
Across the table: the trend depends on shell and subshell.
Periods 1-3 (s and p only): As we go across the table in periods 1-3, the shell stays constant as Z increases and subshell changes from s to p. In these periods, there is a gradual increase in valence \(Z_{eff}\) as we move across any of the first three periods.
Periods 4 and 5 (s, p, and d): Now we have some more complex trends because valence subshell and shell are changing as we increase in atomic number. Notice that the valence \(Z_{eff}\) generally increases going across a period as long as subshell isn't changing; the exception is within the 4d subshell (elements 39-44 or Y-Ru). In general, going from \((n)s\) subshell to \((n-1)d\) subshell, there a relatively large increase in valence \(Z_{eff}\). And in going from \((n-1)d\) subshell to \((n)p\) subshell, there is a relatively large decrease in \(Z_{eff}\).
From one period to another: From Figure \(\PageIndex{4}\), we can see that as we increase Z by one proton, going from one period to the next, there is a relatively large decrease in \(Z_{eff}\) (from Ne to Na, for example). This is because as Z increases by a small interval, the shell number increases, and so the electrons in the valence shell are much farther from the nucleus and are more shielded by all the electrons in the lower shell numbers.
Exercises
1. Compare trends in \(Z_{eff}\) and atomic size. Explain how and why atomic size depends on \(Z_{eff}\).
2. Compare trends in \(Z_{eff}\) and ionization energy. Explain how and why ionization energy depends on \(Z_{eff}\).
- Answer
-
1. As \(Z_{eff}\) increases, the valence electrons are pulled in tighter to the nucleus resulting in a small radius for atoms.
2. As \(Z_{eff}\) increases, the distance between the valence electrons and the nucleus decreases. This creates a stronger force holding the valence electrons, and thus requires a higher ionization energy to remove a valence electron.
Contributors and Attributions
Emily V Eames (City College of San Francisco)
Curated or created by Kathryn Haas