1.1.3: Shielding and Penetration
- Page ID
- 195507
Introduction
Coulomb's Law explains why electrons in different shells (n), at different distances from the nucleus, have different energies. But on its own, Coulomb's law doesn't quite explain why electrons in different subshells would have different energies: For example, why is it that subshells 3s and 3p orbitals have identical energies in a hydrogen (H) atom, but different energies in multi-electron atoms? To answer this question, we'll need to consider how both electron shielding and penetration result in different \(Z_{eff}\) in different subshells, like 3s and 3p. The plots of radial distribution functions (you saw these in the Pre-Semester Reading assignments!) are a helpful tool for visualizing penetration.
Shielding:
Shielding is the reduction of true nuclear charge (Z) to the effective nuclear charge (\(Z_{eff}\)) by other electrons in a multi-electron atom or ion. Shielding occurs in all elements except H.
Explanation of shielding: Electrons in a multi-electron atom interact with the nucleus and all other electrons in the atom. To describe shielding, we can use a simplified model of the atom: we will choose an electron-of-interest in a multi-electron atom, and treat all the "other" electrons as a group of spherically distributed negative charge. Classical electrostatics allows us to treat spherical distribution of charge as a point of charge at the center of the distribution. Thus, classical electrostatics allows us to consider all the "other" electrons in our atom as a point of negative charge in the center of the atom. While the positive charge of the nucleus provides an attractive force toward our electron, the negative charge at the center of the atom would provide a repulsive force. The attractive and repulsive forces would cancel each other; but since there are less "other" electrons than there are protons in our atom, the nuclear charge is never completely canceled. The "other" electrons partially block, or shield, part of the nuclear charge so that our electron-of-interest experiences a partially-reduced nuclear charge, the \(Z_{eff}\).
In reality, there is not a one-for-one "canceling" of the nuclear charge by each electron. Partly due to penetration, no one electron can completely shield a full unit of positive charge. Core electrons shield valence electrons, but valence electrons have little effect on the \(Z_{eff}\) of core electrons. The ability to shield, and be shielded by, other electrons strongly depends the electron orbital's average distance from the nucleus and its penetration; thus shielding depends on both shell (\(n\)) and subshell (\(l\)).
Orbital Penetration: some electrons can get closer than others!
Coulomb's law shows us that distance of an electron from its nucleus is important in determining the electron's energy (its attraction to the nucleus). The shell number (\(n\)) determines approximately how far an electron is from the nucleus on average. Thus, all orbitals in the same shell (s,p,d) have similar sizes and similar average distance of their electrons from the nucleus. But there is another distance-related factor that plays a critical role in determining orbital energy levels: penetration. Penetration describes the ability of an electron in a given subshell to penetrate within other shells and subshells to get close to the nucleus. Penetration is the extent to which an electron can approach the nucleus. Penetration depends on both the shell (\(n\)) and subshell (\(l\)).
The penetration of individual orbitals can be visualized using the radial probability functions. For example, Figure \(\PageIndex{1}\) below shows plots of the radial probability function of the 1s, 2s, and 2p orbitals. From these plots, we can see that the 1s orbital is able to approach closest to the nucleus; thus it is the most penetrating. While the 2s and 2p have most of their probability at a farther distance from the nucleus (compared to 1s), the 2s orbital and the 2p orbital have different extents of penetration. Notice that the 2s orbital is able to penetrate the 1s orbital because of the central 2s lobe. The 2p orbital penetrates somewhat into the 1s, but it cannot approach the nucleus as closely as the 2s orbital can. While the 2s orbital penetrates more than 2p (2s orbital can approach closer to the nucleus), 2p is slightly closer on average than 2s. The order of \(Z_{eff}\) in 2s and 2p subshells depends on which factor (average distance or penetration) is more important. In the first two rows of the periodic table, penetration is the dominant factor that results in 2s having a lower energy compared to 2p.
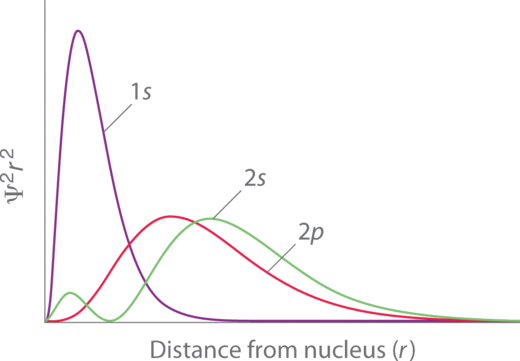
Figure \(\PageIndex{1}\). Orbital Penetration. A comparison of the radial probability distribution of the 2s and 2p orbitals for various states of the hydrogen atom shows that the 2s orbital penetrates inside the 1s orbital more than the 2p orbital does. Consequently, when an electron is in the small inner lobe of the 2s orbital, it experiences a relatively large value of \(Z_{eff}\), which causes the energy of the 2s orbital to be lower than the energy of the 2p orbital.
An electron orbital's penetration effects its ability to shield other electrons and effects the extent to which it is shielded by other electrons. In general, electron orbitals that have greater penetration experience stronger attraction to the nucleus and less shielding by other electrons; these electrons thus experience a larger (\(Z_{eff}\)). Electrons in orbitals that have greater penetration also shield other electrons to a greater extent.
Within the same shell value (n), the penetrating power of an electron follows this trend in subshells (ml):
s>p>d>f
Exercises
- Compare the 2s and 2p orbitals:
(a) Which is closer to the nucleus on average?
(b) Which is more penetrating?
(c) Which orbital experiences a stronger \(Z_{eff}\) and is thus lower in energy (consider your experience, but also inspect Figures 1.1.2.3 and 1.1.2.4 from the previous page)? Please explain. - Peruse the Hyperphysics page (click) that shows radial probability functions of several orbitals (click around on various orbitals). Compare the 2p and 3s orbitals:
(a) Which is farther from the nucleus on average?
(b) Which is more penetrating?
(c) which orbital is lower in energy? - Which atom, Li, or N, has a stronger valence \(Z_{eff}\)? Explain why.
- Explain why 2s and 2p subshells are completely degenerate in a hydrogen atom.
- Which atom has a smaller radii: Be or F? Explain.
- Which electrons shield others more effectively: 3p or 3d?
- Use the clues given in the figures below to label the radial distribution functions shown.

8. Examine the plot below. Notice that the probability density plots for the 3s, 3p, and 3d subshells are highlighted.
(a) For which of these three functions is the highest probability density at the smallest \(r\) value (which closest to the nucleus on average)? Is this the same subshell that penetrates most?
(b) Use this example to describe how penetration and shielding result in a splitting of subshell energy level in multi-electron atoms.
9. Explain why the ground state (most energetically favorable) electron configuration of Be is 1s22s2 rather than alternative configurations like 1s22s12p1 or 1s22p2.
- Answer 1
-
(a) The 2s orbital is closer to the nucleus on average.
(b) The 2s orbital is more penetrating than 2p.
(c) You might "know" that the 2s orbital is lower in energy than 2p because 2s fills first. But a close inspection of Figures 1.1.2.3 and 1.1.2.4 from the previous page indicates that the 2s and 2p elements are degenerate in Ne (element 10), while in elements with atomic number 11 and greater, 2p has a higher \(Z_{eff}\) than 2s! This example illustrates that both average distance and penetration are factors in determining \(Z_{eff}\), and the one that is more important may change as we increase in atomic number.
- Answer 2
-
(a) The 3s orbital reaches farther away from the nucleus and is on average farther from the nucleus than 2p.
(b) The 3s orbital is more penetrating than 2p, even though 3s is farther on average!
(c) The 2p orbital is lower in energy than 3s; this is because 2p is still significantly closer to the nucleus on average and experiences a stronger \(Z_{eff}\). (Penetration is not the only consideration!)
- Answer 3
-
A nitrogen atom has a stronger effective nuclear charge than lithium due to its greater number of protons; even though N also has more electrons that would shield the nuclear charge, each electron only partially shields each proton. This means that atoms with greater atomic number always have greater \(Z_{eff}\) for any given electron.
- Answer 4
-
The hydrogen atom has only one electron; thus there is no shielding to consider. When there are not other electrons to shield the nucleus, penetration and shielding are irrelevant, and subshells within a shell are degenerate.
- Answer 5
-
Fluorine has a smaller radii than Beryllium due to F having a greater valence \(Z_{eff}\) and therefore pulling the valence electrons close to the nucleus and providing a smaller atomic radii.
- Answer 6
-
3p shields better than 3d, because p orbitals penetrate more than d orbitals within the same shell.
- Answer 7
-

- Answer 8
-
3d is closest on average, but 3s penetrates most. The three subshells of \(n=3\) differ in their average distance and in their ability to penetrate; these factors result in differences in the \(Z_{eff}\) experienced by electrons in each orbital. We would expect 3s to be lowest in energy followed by 3p and then 3d.
- Answer 9
-
This question is asking why the 2s orbital fills in Be before 2p is occupied. This is a multi-electron atom, therefore core electrons shield the 2s and 2p orbitals to different extents. In Be we expect the 2s orbital to fill before 2p because 2s penetrates more and experiences a higher \(Z_{eff}\).
References
- Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, and Jeffry D. Madura. General Chemistry: Principles and Modern Applications, Ninth Edition. Pearson Education Inc. Upper Saddle River, New Jersey: 2007.
- Raymond Chang. Physical Chemistry for Biological Sciences. Sausalito, California: University Science Books, 2005
- R. S. Mulliken, Electronic Structures of Molecules and Valence. II General Considerations, Physical Review, vol. 41, pp. 49-71 (1932)
- Anastopoulos, Charis (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 236–237. ISBN 0691135126. http://books.google.com/?id=rDEvQZhpltEC&pg=PA236.


