5.3: Photoelectron Spectroscopy
- Page ID
- 25383
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Photoelectron spectroscopy utilizes photo-ionization and analysis of the kinetic energy distribution of the emitted photoelectrons to study the composition and electronic state of the surface region of a sample. Traditionally, when the technique has been used for surface studies it has been subdivided according to the source of exciting radiation into:
- X-ray Photoelectron Spectroscopy (XPS): using soft x-rays (with a photon energy of 200-2000 eV) to examine core-levels.
- Ultraviolet Photoelectron Spectroscopy (UPS): using vacuum UV radiation (with a photon energy of 10-45 eV) to examine valence levels.
The development of synchrotron radiation sources has enabled high resolution studies to be carried out with radiation spanning a much wider and more complete energy range ( 5 - 5000+ eV ) but such work remains a small minority of all photoelectron studies due to the expense, complexity and limited availability of such sources.
Physical Principles
Photoelectron spectroscopy is based upon a single photon in/electron out process and from many viewpoints this underlying process is a much simpler phenomenon than the Auger process. The energy of a photon of all types of electromagnetic radiation is given by the Einstein relation:
\[E = h \nu \label{5.3.1}\]
where \(h\) is Planck constant ( 6.62 x 10-34 J s ) and \(\nu\) is the frequency (Hz) of the radiation.
Photoelectron spectroscopy uses monochromatic sources of radiation (i.e. photons of fixed energy). In XPS, the photon is absorbed by an atom in a molecule or solid, leading to ionization and the emission of a core (inner shell) electron. By contrast, in UPS the photon interacts with valence levels of the molecule or solid, leading to ionization by removal of one of these valence electrons. The kinetic energy distribution of the emitted photoelectrons (i.e. the number of emitted photoelectrons as a function of their kinetic energy) can be measured using any appropriate electron energy analyzer and a photoelectron spectrum can thus be recorded. The process of photoionization can be considered in several ways: one way is to look at the overall process as follows:
\[A + hν \rightarrow A^+ + e^- \label{5.3.2}\]
Conservation of energy then requires that:
\[E(A) + h\nu = E(A^+ ) + E(e^-) \label{5.3.3}\]
Since the electron's energy is present solely as kinetic energy (KE) this can be rearranged to give the following expression for the KE of the photoelectron:
\[KE = h\nu - ( E(A^+ ) - E(A) )\label{5.3.4}\]
The final term in brackets, representing the difference in energy between the ionized and neutral atoms, is generally called the binding energy (BE) of the electron - this then leads to the following commonly quoted equation:
\[KE = h\nu - BE \label{5.3.5}\]
An alternative approach is to consider a one-electron model along the lines of the following pictorial representation; this model of the process has the benefit of simplicity but it can be rather misleading.

The BE is now taken to be a direct measure of the energy required to just remove the electron concerned from its initial level to the vacuum level and the KE of the photoelectron is again given by:
\[KE = hν - BE \label{5.3.6}\]
The binding energies (BE) of energy levels in solids are conventionally measured with respect to the Fermi level of the solid, rather than the vacuum level. This involves a small correction to Equation \ref{5.3.6} to account for the work function (\(φ\)) of the solid. For the purposes of the discussion below this correction will be neglected.
Experimental Details
The basic requirements for a photoemission experiment (XPS or UPS) are:
- a source of fixed-energy radiation (an x-ray source for XPS or, typically, a He discharge lamp for UPS)
- an electron energy analyser (which can disperse the emitted electrons according to their kinetic energy, and thereby measure the flux of emitted electrons of a particular energy)
- a high vacuum environment (to enable the emitted photoelectrons to be analyzed without interference from gas phase collisions)
Such a system is illustrated schematically below:
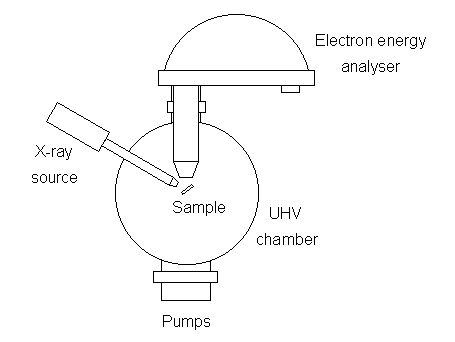
There are many different designs of electron energy analyzer but the preferred option for photoemission experiments is a concentric hemispherical analyser (CHA) which uses an electric field between two hemispherical surfaces to disperse the electrons according to their kinetic energy.
X-ray Photoelectron Spectroscopy (XPS)
For each and every element, there will be a characteristic binding energy associated with each core atomic orbital i.e. each element will give rise to a characteristic set of peaks in the photoelectron spectrum at kinetic energies determined by the photon energy and the respective binding energies. The presence of peaks at particular energies therefore indicates the presence of a specific element in the sample under study - furthermore, the intensity of the peaks is related to the concentration of the element within the sampled region. Thus, the technique provides a quantitative analysis of the surface composition and is sometimes known by the alternative acronym, ESCA (Electron Spectroscopy for Chemical Analysis). The most commonly employed x-ray sources are those giving rise to:
- Mg Kα radiation: hν = 1253.6 eV
- Al Kα radiation: hν = 1486.6 eV
The emitted photoelectrons will therefore have kinetic energies in the range of ca. 0 - 1250 eV or 0 - 1480 eV. Since such electrons have very short IMFPs in solids (Section 5.1), the technique is necessarily surface sensitive.
The diagram below shows a real XPS spectrum obtained from a Pd metal sample using Mg Kα radiation
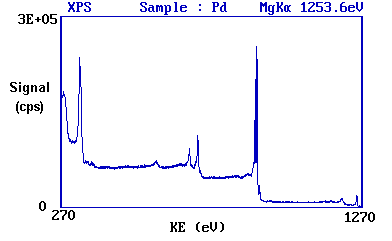
- the main peaks occur at kinetic energies of ca. 330, 690, 720, 910 and 920 eV.
Since the photon energy of the radiation is always known it is a trivial matter to transform the spectrum so that it is plotted against BE as opposed to KE.
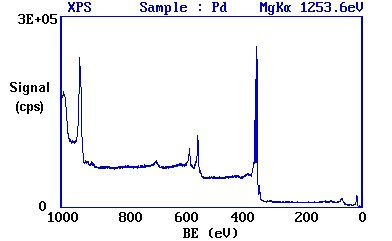
The most intense peak is now seen to occur at a binding energy of ca. 335 eV
Working downwards from the highest energy levels ......
- the valence band (4d, 5s) emission occurs at a binding energy of ca. 0 - 8 eV ( measured with respect to the Fermi level, or alternatively at ca. 4 - 12 eV if measured with respect to the vacuum level ).
- the emission from the 4p and 4s levels gives rise to very weak peaks at 54 eV and 88 eV respectively
- the most intense peak at ca. 335 eV is due to emission from the 3d levels of the Pd atoms, whilst the 3p and 3s levels give rise to the peaks at ca. 534/561 eV and 673 eV respectively.
- the remaining peak is not an XPS peak at all ! - it is an Auger peak arising from x-ray induced Auger emission. It occurs at a kinetic energy of ca. 330 eV (in this case it is really meaningless to refer to an associated binding energy).
These assignments are summarized below ...
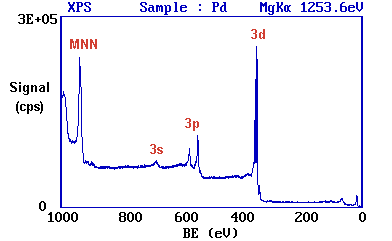
It may be further noted that
- there are significant differences in the natural widths of the various photoemission peaks
- the peak intensities are not simply related to the electron occupancy of the orbitals
The diagram opposite shows an energy level diagram for sodium with approximate binding energies for the core levels.
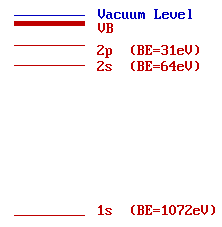
If we are using Mg Kα ( hν = 1253.6 eV ) radiation ...
![]() ... at what kinetic energy will the Na 1s photoelectron peak be observed ?
... at what kinetic energy will the Na 1s photoelectron peak be observed ?
(the 1s peak is that resulting from photoionisation of the 1s level)
![]() ... at what kinetic energy will the Na 2s and 2p photoelectron peaks be observed ?
... at what kinetic energy will the Na 2s and 2p photoelectron peaks be observed ?
Spin-Orbit Splitting
Closer inspection of the spectrum shows that emission from some levels (most obviously 3p and 3d ) does not give rise to a single photoemission peak, but a closely spaced doublet. We can see this more clearly if, for example, we expand the spectrum in the region of the 3d emission ...
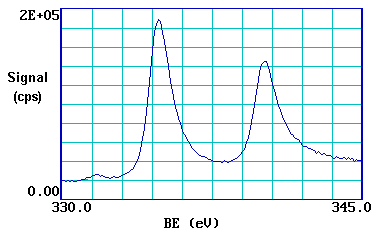
The 3d photoemission is in fact split between two peaks, one at 334.9 eV BE and the other at 340.2 eV BE, with an intensity ratio of 3:2 . This arises from spin-orbit coupling effects in the final state. The inner core electronic configuration of the initial state of the Pd is:
(1s)2 (2s)2 (2p)6 (3s)2 (3p)6 (3d)10 ....
with all sub-shells completely full.
The removal of an electron from the 3d sub-shell by photo-ionization leads to a (3d)9 configuration for the final state - since the d-orbitals ( l = 2) have non-zero orbital angular momentum, there will be coupling between the unpaired spin and orbital angular momenta. Spin-orbit coupling is generally treated using one of two models which correspond to the two limiting ways in which the coupling can occur - these being the LS (or Russell-Saunders) coupling approximation and the j-j coupling approximation. If we consider the final ionised state of Pd within the Russell-Saunders coupling approximation, the (3d)9 configuration gives rise to two states (ignoring any coupling with valence levels) which differ slightly in energy and in their degeneracy ...
|
2D 5/2 |
gJ = 2x{5/2}+1 = 6 |
|
2D 3/2 |
gJ = 2x{3/2}+1 = 4 |
These two states arise from the coupling of the L = 2 and S = 1/2 vectors to give permitted J values of 3/2 and 5/2. The lowest energy final state is the one with maximum J (since the shell is more than half-full), i.e. J = 5/2, hence this gives rise to the "lower binding energy" peak. The relative intensities of the two peaks reflects the degeneracies of the final states (gJ = 2J + 1), which in turn determines the probability of transition to such a state during photoionization.
The Russell-Saunders coupling approximation is best applied only to light atoms and this splitting can alternatively be described using individual electron l-s coupling. In this case the resultant angular momenta arise from the single hole in the d-shell; a d-shell electron (or hole) has l = 2 and s = 1/2, which again gives permitted j-values of 3/2 and 5/2 with the latter being lower in energy.
The peaks themselves are conventionally annotated as indicated - note the use of lower case lettering
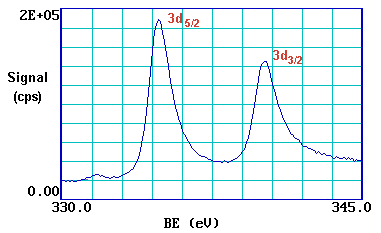
This spin-orbit splitting is of course not evident with s-levels (l = 0), but is seen with p,d & f core-levels which all show characteristic spin-orbit doublets.
Chemical Shifts
The exact binding energy of an electron depends not only upon the level from which photoemission is occurring, but also upon both the formal oxidation state of the atom and the local chemical and physical environment. Changes in either give rise to small shifts in the peak positions in the spectrum - so-called chemical shifts. Such shifts are readily observable and interpretable in XP spectra (unlike in Auger spectra) because the technique is of high intrinsic resolution (as core levels are discrete and generally of a well-defined energy) and is a one electron process (thus simplifying the interpretation).
Atoms of a higher positive oxidation state exhibit a higher binding energy due to the extra coulombic interaction between the photo-emitted electron and the ion core. This ability to discriminate between different oxidation states and chemical environments is one of the major strengths of the XPS technique. In practice, the ability to resolve between atoms exhibiting slightly different chemical shifts is limited by the peak widths which are governed by a combination of factors; especially
- the intrinsic width of the initial level and the lifetime of the final state
- the line-width of the incident radiation - which for traditional x-ray sources can only be improved by using x-ray monochromators
- the resolving power of the electron-energy analyser
In most cases, the second factor is the major contribution to the overall line width.
Titanium exhibits very large chemical shifts between different oxidation states of the metal; in the diagram below a Ti 2p spectrum from the pure metal (Tio ) is compared with a spectrum of titanium dioxide (Ti4+ ).
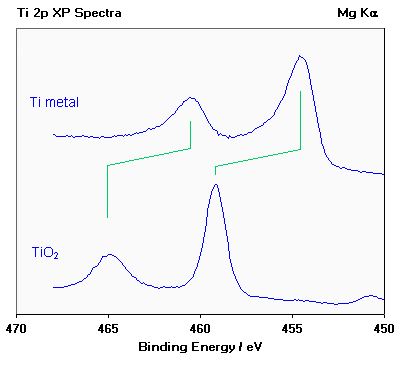 Oxidation states of titanium [Ti 2p spectra].
Oxidation states of titanium [Ti 2p spectra].
Note
- the two spin orbit components exhibit the same chemical shift (∼ 4.6 eV);
- metals are often characterised by an asymmetric line shape, with the peak tailing to higher binding energy' whilst insulating oxides give rise to a more symmetric peak profile;
- the weak peak at ca. 450.7 eV in the lower spectrum arises because typical x-ray sources also emit some x-rays of a slightly higher photon energy than the main Mg Kα line; this satellite peak is a "ghost" of the main 2p3/2 peak arising from ionisation by these additional x-rays.
Angle Dependent Studies
As described previously, the degree of surface sensitivity of an electron-based technique such as XPS may be varied by collecting photoelectrons emitted at different emission angles to the surface plane. This approach may be used to perform non-destructive analysis of the variation of surface composition with depth (with chemical state specificity).
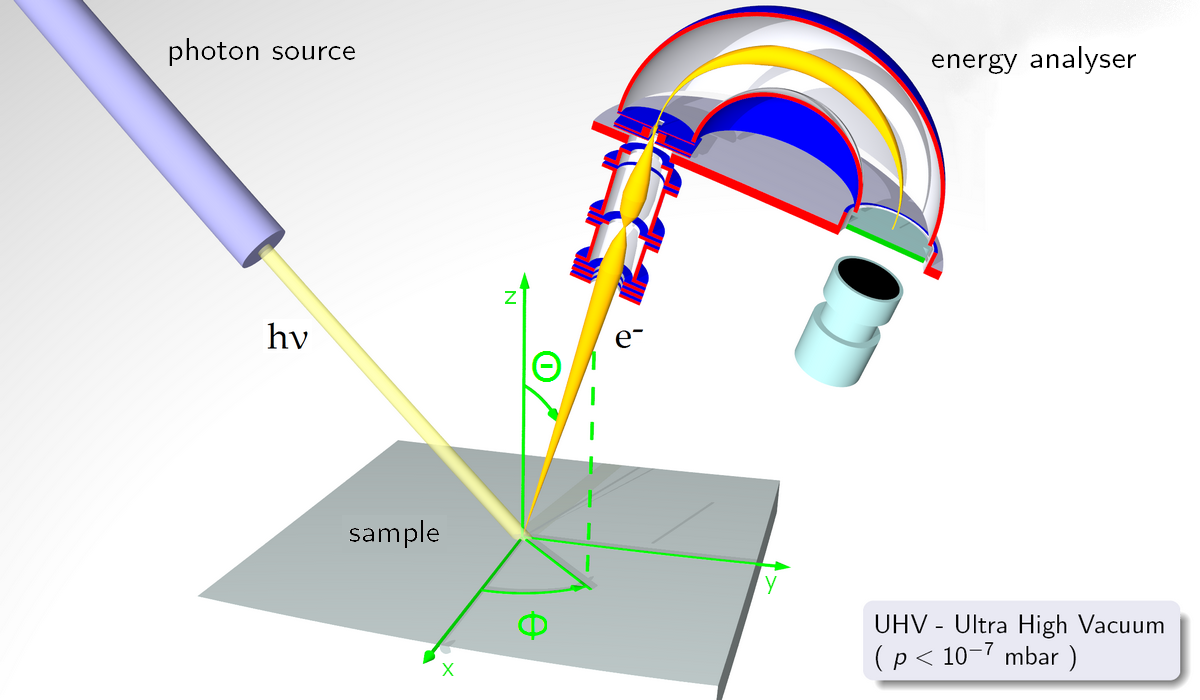
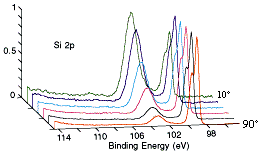
A series of Si 2p photoelectron spectra recorded for emission angles of 10-90º to the surface plane. Note how the Si 2p peak of the oxide (BE ~ 103 eV) increases markedly in intensity at grazing emission angles whilst the peak from the underlying elemental silicon (BE ~ 99 eV) dominates the spectrum at near-normal emission angles.
(courtesy of Physical Electronics, Inc. (PHI))
Note: in this instance the emission angle is measured with respect to the surface plane (i.e. 90º corresponds to photoelectrons departing with a trajectory normal to the surface, whilst 10º corresponds to emission at a very grazing angle;
Ultraviolet Photoelectron Spectroscopy (UPS)
In UPS the source of radiation is normally a noble gas discharge lamp; frequently a He-discharge lamp emitting He I radiation of energy 21.2 eV. Such radiation is only capable of ionizing electrons from the outermost levels of atoms - the valence levels. The advantage of using such UV radiation over x-rays is the very narrow line width of the radiation and the high flux of photons available from simple discharge sources. The main emphasis of work using UPS has been in studying:
- the electronic structure of solids - detailed angle resolved studies permit the complete band structure to be mapped out in k-space.
- the adsorption of relatively simple molecules on metals - by comparison of the molecular orbitals of the adsorbed species with those of both the isolated molecule and with calculations.


