5.1: Surface Sensitivity and Surface Specificity
- Page ID
- 25381
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)General Sensitivity Problems
The problems of sensitivity and detection limits are common to all forms of spectroscopy; some techniques are simply better than others in this respect! In its simplest form, the question of sensitivity boils down to whether it is possible to detect the desired signal above the noise level.
In virtually all surface studies (especially those on single crystal substrates) sensitivity is a major problem. Consider the case of a sample with a surface of size 1 cm2 - this will have ca. 1015 atoms in the surface layer. In order to detect the presence of impurity atoms present at the 1 % level, a technique must be sensitive to ca. 1013 atoms. Contrast this with a spectroscopic technique used to analyze a 1 cm3 bulk liquid sample i.e. a sample of ca. 1022 molecules. The detection of 1013 molecules in this sample would require 1 ppb (one part-per-billion) sensitivity - very few techniques can provide anything like this level of sensitivity! This is one reason why common spectroscopic techniques such as NMR (detection limit ca. 1019 molecules) cannot be used for surface studies, except on samples with very high surface areas.
Surface Sensitivity & Specificity
Assuming that a technique of sufficient sensitivity can be found, another major problem that needs to be addressed in surface spectroscopy is distinguishing between signals from the surface and the bulk of the sample. In principle, there are two ways around this problem:
- To ensure that the surface signal is distinguishable (shifted) from the comparable bulk signal, and that the detection system has sufficient dynamic range to detect very small signals in the presence of neighboring large signals.
- To ensure that the bulk signal is small compared to the surface signal i.e. that the vast majority of detected signal comes from the surface region of the sample.
It is the latter approach which is used by the majority of surface spectroscopic techniques - such techniques can then be said to be surface sensitive. To illustrate this, we shall look at one way in which surface sensitivity can be achieved - this makes use of the special properties of Low Energy Electrons. It is an approach employed in common surface spectroscopic techniques such as Auger Electron Spectroscopy (AES) and X-ray Photoelectron Spectroscopy (XPS).
We shall illustrate this approach by considering the latter technique (XPS) but you should remember that the ideas that we develop are more widely applicable.
XPS - A surface sensitive technique?
In answering this important question, we will actually address the topics listed below - you are strongly advised to work through them in the order in which they are given.
- What do we really mean by surface sensitivity / specificity ?
- How can we demonstrate that XPS is surface sensitive ?
- Why is the XPS technique surface sensitive ?
- How can we use knowledge of the IMFP to calculate the thickness of surface films ?
- How can we change the degree of surface sensitivity ?
What do we really mean by surface sensitivity / specificity?
Most analytical techniques used in chemistry are "bulk" techniques in the sense that they measure all the atoms within a typical sample (be it a solid, liquid, solution or gas phase sample) - so if, for example, we were to analyse a sample consisting of a 10 nm thick layer of one material (A) deposited on a 1 mm thick substrate of another material (B) ....
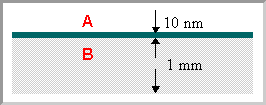
… and to ask the question ….
What would be the concentration of A in parts per million (ppm) which you would expect to be revealed by a bulk analysis of such a sample ?
.... we would get the same result (10 ppm) as if we were looking at a sample in which component A was uniformly distributed throughout the bulk of B such as to give the same overall concentration in the sample as a whole.

By contrast, a surface sensitive technique is more sensitive to those atoms which are located near the surface than it is to atoms in the bulk which are well away from the surface (i.e. the main part of the signal comes from the surface region) - in the case of the first sample therefore a surface sensitive technique would produce a spectrum with enhanced signals due to component A, i.e.
\[\dfrac{I_A}{I_B} \gg 10^{-5}\]
where \(I_A\) is the signal due to component A etc.
A truly surface specific technique should only give signals due to atoms in the surface region - but that, of course, rather depends how the "surface region" is defined!
Electron spectroscopic techniques such as XPS are not completely surface specific (although you will occasionally find this expression being used) in that whilst most of the signal comes from within a few atomic layers of the surface, a small part of the signal comes from much deeper into the solid - they are best described as being surface sensitive techniques. However, we should also note that there are a few techniques (e.g. low energy ion scattering [ISS/LEIS]) which are indeed virtually specific to the topmost layer of atoms.
How can we demonstrate that XPS is surface sensitive ?
Consider again the first of the two samples considered in the previous section - such samples are often readily prepared by depositing material A by evaporation onto a substrate of material B.
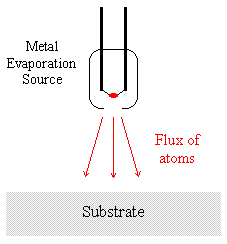
It is experimentally observed that in such a situation the XPS signals due to the substrate (material B) are rapidly attenuated, whilst those due to the condensed evaporant (material A) simultaneously increase to a limiting value.
It is possible to measure deposition rates using equipment such as quartz crystal oscillators and thus obtain independent verification of the deposited film thickness. A detailed analysis of the variation of the signals due to A and B is also capable of yielding information about the mechanism of film growth.
Why is the XPS technique surface sensitive ?
The soft X-rays employed in XPS penetrate a substantial distance into the sample (~µm). Thus this method of excitation imparts no surface sensitivity at the required atomic scale. The surface sensitivity must therefore arise from the emission and detection of the photoemitted electrons. Consider, therefore, a hypothetical experiment in which electrons of a given energy, E0 , are emitted from atoms in a solid at various depths, d, below a flat surface.
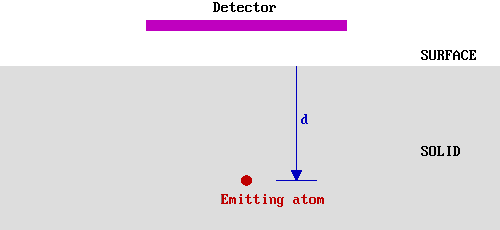
We shall assume that only those electrons which reach the surface and, at the time of leaving the solid, still have their initial energy (Eo ) are detected in this experiment. This is not literally true in an XPS experiment, but in XPS experiments it is only those photoelectrons possessing characteristic emission energies and contributing to the peaks and that we consider in the subsequent analysis; we do not consider photoelectrons which have lost some energy and contribute to the background of the spectrum rather than a specific peak.
There are two things which would therefore prevent an emitted electron from being detected:
- If it were "captured" before reaching the surface, or emitted in the wrong direction and never reached the surface !
- If it lost energy before reaching the surface, i.e. if it escaped from the solid and reached the detector, but with E < Eo
The process by which an electron can lose energy as it travels through the solid is known as "inelastic scattering". Each inelastic scattering event leads to: (i) a reduction in the electron energy (ii) a change in the direction of travel.
In the diagram below arrows are used to represent possible trajectories of emitted electrons from a particular source atom. The orange arrows represent electrons travelling with their initial energy, Eo, whilst the blue arrows represent electron trajectories subsequent to an inelastic scattering event. Only the orange traces which extend out of the solid therefore correspond to electrons which would be detected in our hypothetical experiment.
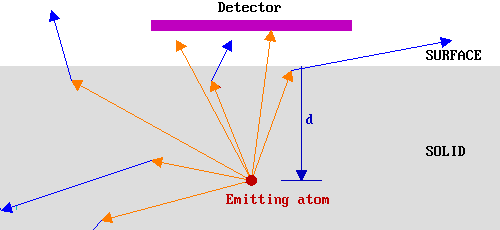
In this case, therefore, only a small fraction of the emitted electrons would have been detected. Clearly if the source atom had been closer to the surface, then a greater fraction of the emitted electrons would have been detected since:
- The detector would subtend a greater (solid) angle at the emitting atom (this is actually not a significant factor in real experiments).
- For an electron emitted towards the surface, there would be less chance of inelastic scattering before it escaped from the solid.
So how does the probability of detection depend upon the distance of the emitting atom below the surface ?
Let us first simplify the problem by only considering those electrons emitted directly towards (normal to) the surface - in our hypothetical experiment we can represent this by a smaller detector located directly above the emitting atoms.
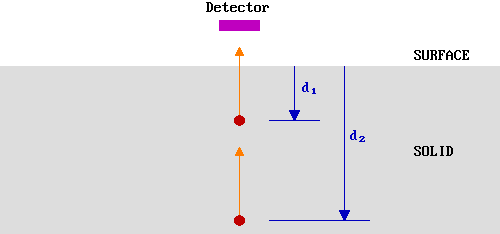
The probability of escape from a given depth, \(P(d)\), is determined by the likelihood of the electron not being inelastically scattered during its journey to the surface.
Clearly, \(P(d_2 ) < P(d_1 )\) but, in order to quantify this we need to know more about the inelastic scattering process - this brings us to the subject of the ..
Inelastic Mean Free Path (IMFP) of electrons.
The IMFP is a measure of the average distance travelled by an electron through a solid before it is inelastically scattered; it is dependent upon
- The initial kinetic energy of the electron.
- The nature of the solid ( but most elements show very similar IMFP v's energy relationships).
The IMFP is actually defined by the following equation which gives the probability of the electron travelling a distance, d, through the solid without undergoing scattering
\[P(d) = exp ( \frac{- d}{λ} ) \]
where \(λ\) is the IMFP for the electrons of energy E. (Note: λ = f(E), and this inelastic mean free path, which relates to the movement of electrons in the solid, is completely unrelated to the mean free path in the gas phase once they escape from the solid).
The graph below illustrates this functional form of \(P(d)\) …
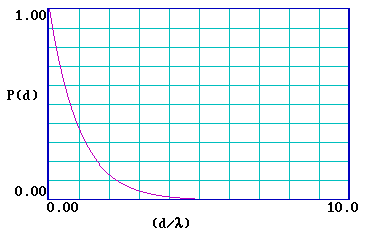
… and it is clear that the probability of escape decays very rapidly and is essentially zero for a distance d > 5λ . It is therefore useful to re-plot the function for a range of (d/λ) from 0-5 .
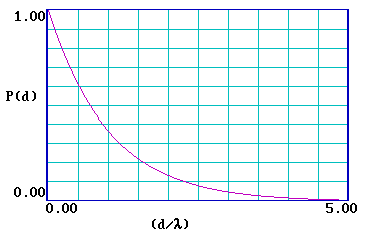
|
|
What is the probablility of escape when … d = 1λ ? |
|
|
What is the probablility of escape when … d = 2λ ? |
|
|
What is the probablility of escape when … d = 3λ ? |
It is also interesting to look at this same problem from a different point of view. Let us assume that there are many sources of electrons uniformly distributed at all distances from the surface of the solid (which is in effect the situation pertaining in all XPS experiments) and again arrange to only detect those unscattered electrons which emerge normal to the surface - then we can ask ...
What is the distribution of the depths of origin of those electrons that we do detect ?
This new function, let's call it P'(d), actually has the same exponential form as P(d) - i.e. the frequency of detection of electrons from different depths in the solid is directly proportional to the probability of electron escape from each depth.
So if we allow our detector to collect 100 electrons, we can ask how many electrons (on average) will have come from within a distance of one IMFP from the surface (i.e. how many originate from a distance, \(d\), such that \(0 < (d/λ) < 1\))?
This is a relatively simple problem in integration - try it !
- Answer
-
In summary, we can conclude from the answer to this question that the majority of electrons detected come from within one "imfp" of the surface. Virtually all ( > 95% ) of the electrons detected come from within 3 IMFPs of the surface.
Beware of terms such as "sampling depth " and "electron escape depth ". It is not always clear whether these refer to 1, 3 or 5 IMFPs (or something else completely).
So how big is the IMFP of typical electrons within a solid such as a metal ?
The graph below shows the so-called "universal curve" for the variation of the IMFP with initial electron energy (in eV ).
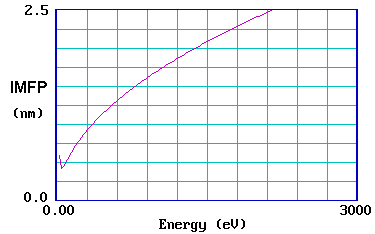
It is reasonably accurate for most metals, although experimental measurements on different metals do show a substantial scatter about the general curve.
Other classes of solids also exhibit qualitatively similar universal curves, although the absolute values of the IMFP of electrons in materials such as inorganic solids and polymers do differ quite significantly from those in metals.
This IMFP data is more usually displayed on a log-log plot, since this more clearly shows how the IMFP varies at low kinetic energies - the graph below shows the general curve for metals re-plotted in this new format.
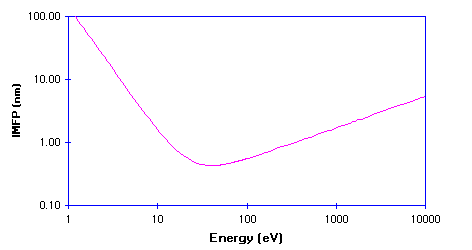
The IMFP exhibits a minimum for electrons with a kinetic energy of around 50 -100 eV ; at lower energies the probability of inelastic scattering decreases since the electron has insufficient energy to cause plasmon excitation (the main scattering mechanism in metals), and consequently the distance between inelastic collisions and the IMFP increases.
Summary
The Inelastic Mean Free Path (IMFP) in metals is typically less than:
- 10 Angstroms ( 1 nm ) for electron energies in the range 15 < E/eV < 350
- 20 Angstroms ( 2 nm ) for electron energies in the range 10 < E/eV < 1400
i.e. the IMFP of low energy electrons corresponds to only a few atomic layers. This means that any experimental technique such as XPS which involves the generation and detection of electrons of such energies will be surface sensitive.
How can we use knowledge of the IMFP to calculate the thickness of surface films ?
We can now consider a situation where a substrate (or thick film) of one material, B, is covered by a thin film of a different material, A . The XPS signal from the underlying substrate will be attenuated (i.e. reduced in intensity) due to inelastic scattering of some of the photoelectrons as they traverse through the layer of material A .
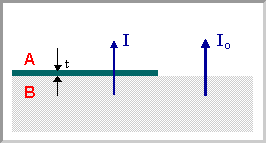
For any single photoelectron, the probability of the electron passing through this overlayer without being subject to a scattering event is given by:
\[P = exp ( \frac{- t}{λ} )\]
where \(t\) is the thickness of the layer of material A .
It follows that the overall intensity of the XPS signal arising from B is reduced by this same factor, i.e. if the intensity of this signal in the absence of any covering layer is Io then the intensity I in the presence of the overlayer is given by:
\[I = I_o exp ( \frac{ - t}{ λ} )\]
It also follows that it is possible to estimate the thickness of a deposited layer (using the above equation), provided the reduction in the substrate signal is known (i.e. if spectra are acquired before and after deposition of the covering film).
How can we change the degree of surface sensitivity?
For a given technique such as XPS which relies on inelastic electron scattering to provide the surface sensitivity, we can consider how it might be possible to increase the surface sensitivity when analysing a particular substrate.
One approach would be to try and ensure that the electrons being detected have kinetic energies corresponding to the minimum in the universal curve for the IMFP. The problem with this approach is that
- it requires us to be able to vary the X-ray radiation so that we can adjust the photon energy, hν, to give us the desired kinetic energy for the photoemitted electrons ; this is not generally possible with conventional laboratory x-ray sources (although tunable x-ray radiation is available at large synchrotron sources)
- whilst it may be possible to adjust the kinetic energy of some particular photoelectrons to correspond to the minimum in the universal curve, this effect may not hold for all the other photoelectron peaks associated with the sample.
A much more generally useful approach is to collect photoelectrons at a more grazing emission angle.
The key point to recognise here is that it is actually the distance that the electrons have to travel through the solid (rather than the distance of the emitting atom below the surface) that is crucial in determining their probability of escape without inelastic scattering - only in the special case considered previously of normal emission are these two quantities the same.
Consider, for example, emission at some angle θ to the surface normal.
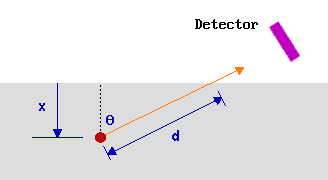
Once again 63% of the electrons will originate from atoms located such that the electrons have to travel a distance, d, which is less than 1λ through the solid (see above). Under these measurement conditions, however, all these atoms are located within a smaller distance, x, from the surface where
\[x = d \cos θ\]
So as the emission angle (θ) is increased, cos θ decreases, the analysed region becomes more surface localised and the surface sensitivity is increased.
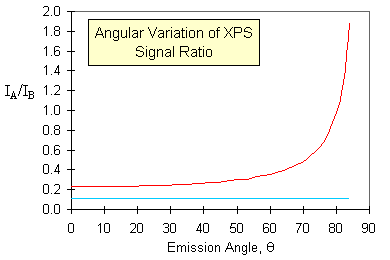
One example of how this effect can be put to good use is in the study (and diagnosis) of surface segregation. The graph below shows simulated data for the variation of the XPS signal intensities with emission angle for
- a random alloy of 10% of element A in element B, with no segregation (lower blue curve)
- the same random alloy, but with surface segregation of A to give a surface monolayer of pure element A (upper red curve)