EXAFS - Theory
- Page ID
- 1867
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)EXAFS (Extended X-ray Absorption Fine Structure) and XANES (X-Ray Absorption Near Edge structure) are regions of the spectrum obtained from XAS(X-ray Absorption Spectroscopy). EXAFS corresponds to the oscillating part of the spectrum to the right of the absorption edge(appearing as a sudden, sharp peak), starting at roughly 50 eV and extending to about 1000 eV above the edge (shown in Figure 1). Through mathematical analysis of this region, one can obtain local structural information for the atom in question.
Introduction
The ability of EXAFS to provide information about an atom's local environment has widespread application, particularly to the geometric analysis of amorphous crystalline solids. Over time, EXAFS has become more applicable to quantitative analysis of noncrystalline materials. When analyzing a single atom within a material, properties analyzed include coordination number, disorder of neighboring atoms, and distance of neighboring atoms. Of these three properties, radial distance is the only property reliably measured. Theoretically obtained structural information becomes more accurate the further down the EXAFS region, ~0.02 Angstroms or better. Experimentally it has also been shown that application of the EXAFS technique is most accurate for systems of low thermal or static disorder.
Qualitative understanding of the EXAFS region
X-Ray spectroscopy involves a process in which an X-ray beam is applied to an atom and causes the ejection of an electron, usually a core electron. This leaves a vacancy in the core shell, and results in relaxation of an outer electron to fill that vacancy. This phenomenon is only observed when the energy of the X-ray exceeds the ionization energy of the electrons in that shell. We can relate this occurrence to the X-ray Absorption coefficient, which becomes the basis of EXAFS theory. The X-ray Absorption coefficient, or μ, describes the relationship between the intensity of an X-ray beam going into a sample and its intensity leaving the sample after traveling a distance x within the sample. The absorption coefficient is given by
\[\mu =-\frac{d lnI}{dx}\]
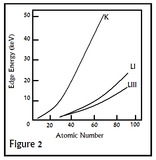
In this expression, dx is the traversed distance, and I is the intensity. In a typical EXAFS spectrum, various sharp peaks will be observed when energy(usually in eV) is plotted against absorbance. These peaks(called edges), which vary by atom, correspond to the ionization of a core orbital, K-edges describing the excitation of the innermost 1s electron, and L-edges and M-edges referring to the same for higher energy orbitals. A qualitative diagram of these energies, as well as their dependence on atomic number, is shown in Figure 2 below.
After each edge, a series of downward oscillations will be observed. These oscillations correspond to wave interactions between the ejected photoelectron and electrons surrounding the absorbing atom. The neighboring atoms are called backscattering atoms, since the waves emitted from the absorbing atom change paths when they hit these neighboring atoms, returning to the original atom. Maxima in the oscillations result from constructive interference between these waves, and minima result from destructive interference. These oscillations are also characteristic of the surrounding atoms and their distances from the central atom, since varying distances will result in different backscattering paths, and as a result different wave interactions. The EXAFS fine structure begins at roughly 30 eV past each edge, where oscillations begin to decay. In addition, this wave interaction will depend on the mechanism of scattering, since the path taken by a wave sometimes involves collision with an intermediate atom, or even multiple atoms, before it reverts to the absorbing atom.
Extraction of Data using the EXAFS Equation
To represent the EXAFS region from the whole spectrum, a function χ can be roughly defined in terms of the absorption coefficient, as a function of energy:
\[\chi (E)=\frac{\mu (E)-\mu _{o}(E)}{\Delta \mu _{o}}\]
Here, the subtracted term represents removal of the background and the division by Δμo represents the normalization of the function, for which the normalization function is approximated to be the sudden increase in the absorption coefficient at the edge. When interpreting data for the EXAFS, it is general practice to use the photoelectron wave vector, k, which is an independent variable that is proportional to momentum rather than energy.
We can solve for k by first assuming that the photon energy E will be greater than E0 (the initial X-ray absorption energy at the edge). Since energy is conserved, excess energy given by E - E0 is conserved by being converted into the kinetic energy of the photoelectron wave. Since wavelengths are dependent on kinetic energies, the photoelectron wave (de Broglie wavelength) will propagate through the EXAFS region with a velocity of ν where the wavelength of the photoelectron will be scanned. This gives the relation, (E - E0) = meν2/2. One of the identities for the de Broglie wavelength is that it is inversely proportional to the photoelectrons momentum (meν): λ=h/meν. Using simple algebraic manipulations, we are able to obtain the following:
\[ k = \dfrac{2\pi}{\lambda} = \dfrac{2\pi m_{e}\nu}{h} = \left[\dfrac{8\pi^2m_{e}(E-E_o)}{h^2}\right]^{\frac{1}{2}} \]
To amplify the oscillations graphically, k is often plotted as k3
Now that we have an expression for k, we begin to develop the EXAFS equation by using Fermi's Golden Rule. This rule states that the absorption coefficient is proportional to the square of the transition moment integral, or |<i|H|f>|2 , where i is the unaffected core energy level before it interferes with the neighboring atoms, H is the interaction, and f is the final state in which the core energy level has been affected and a photoelectron has been ejected. This integral can be related to the total wavefunction Ψk, which represents the sum of all interacting waves, from the backscattering atoms and the absorbing atom. The integral is proportional to the total wavefunction squared, which refers to the probability that the photoelectron is found at the atom where the photon is absorbed, as a function of radius. This wavefunction describes the constructive/destructive nature of the wave interactions within it, and varies depending on the phase difference of the waves interacting. This phase difference can be easily expressed in terms of our photoelectron wave number and R, the distance to the innershell from the wave, as 2k/R. In addition, another characteristic of this wave interaction is the amplitude of waves backscattering to the central atom. This amplitude is can provide coordination number as well since it is thought to be directly proportional to the number of scatters.
The physical description of all these properties is given in a final function for χ(k), called the EXAFS equation:
Looking at the qualitative relationships between the contributions to this equation gives an understanding of how certain factors can be extracted from this equation. In this equation, f(k) represents the amplitude and δ(k) represents the phase shift. Since these two parameters can be calculated for a certain k value, R, N, and σ are our remaining unknowns. These unknown values represent the information we can obtain from this equation: radius, coordination number(number of scattering atoms), and the measure of disorder in neighboring atoms, respectively. These are all also properties of the scattering atom.
We can also see the terms in this equation represented in a typical EXAFS spectrum: the sine term gives the origin of the sinusoid shape, with a greater phase shift making the oscillations greater. In addition, this oscillation depends on the energy and on the radial distance. The Debye-Waller Factor explains the decay with increasing energy, as well as increasing disorder. This factor is partially due to thermal effects. In addition, we deduce the reason why EXAFS does not work over long distances (up to 4-5 Å): the term Rj-2 causes the expression to decrease exponentially over large values of Rj (larger distances between absorbing and scattering atoms), making EXAFS much weaker over long-distances as opposed to short ranged neighboring atoms.
The last step in order to complete the data extraction is to take a Fourier transform of this expression into frequency space, which results in a radial distribution function where peaks correspond to the most likely distances of the nearest-neighbors.
Multiple Scattering
The cases thus far have only dealt with single scattering pathways. Figure 4 shows a scenario in which two scattering atoms (denoted by s) are present with one photoelectron wave source. In this case, what would happen? There is a clear dependence on the distance and angles of the scattering atoms. Thus, it is no longer a simple matter of 1-D space distance relations, but rather a 2-D polar coordinate system. In the case of Cu-Cu (shown by Kroneck et al) the copper is not only the absorbing atom, it is also the scattering atom. Given this paradox, what would happen to the amplitude, phase, and frequency with respect to the two coppers, and with respect to its neighboring atoms?
The effect of multiple scattering is a powerful tool, which is used to determine a variety of information on the local structure. Each individual atom will produce more scattering or absorbing atoms depending on the type of atom and what type of wave hits it. The angle at which the wave scatters back and its distance from the scattering atom will also affect the overall intensity of the EXAFS spectrum. In scenario (a), shown in figure 4, the absorbing atom is hit by an X-ray where it produces an absorbing wave which will scatter off S1 and hit S2. It will then send a scattering wave back to (a), which allows us to obtain further information on the local structure of this molecule. However, this will only work if the absorbing atom is within 4-5 Å away from the scattering atoms. Otherwise, the wave becomes very dampened and the information retrieved becomes very unreliable. In short, multiple scattering effects can be observed, but for the most part, they will only affect the EXAFS spectrum a miniscule (but noticeable) amount. When an absorbing wave goes through another absorbing atom as mentioned in Kroneck et al, it will produce a dampened absorbing wave (due to destructive interference) and give a lower signal than normal. kroneck et al. tested this on two types of systems, the first was a copper single scattering onto a neighboring atom, the second was two coppers scattering onto a scattering atom (all lined up linearly). When both of the radial distances were collected, the second test showed only a small difference (0.02 Å) compared to the first test, suggesting experimentally that multiple scattering waves do have an effect on the determination of a molecular system.
References
- Que, L (2000). Physical Methods in Bioinorganic Chemistry. Sasuolito, California: University Science Books.
- Kroneck, P. M. H., Antholine; W. E.; Kastrau, D. H. W.; Buse. G.; Steffens, G. C. M.; Zumft, W. G., "Multifrequency EPR Evidence for a Bimetallic Centre at the CuA site in Cytochrome c Oxidase." Eur. J. Biochem. 1992, 209, 875-881
- Farrar, J. A.; Lappalainen, P.; Zumft, W. G.; Saraste, M.; Thomson, A. J., "Spectroscopic and Mutagenesis Studies on the CuA centre from the Cytochrome-c Oxidase complex of Paracoccus denitrificans." Eur. J. Biochem. 1996, 232, 294-303
- J.J. Rehr and R.C. Albers, "Theoretical approaches to X-ray absorption fine structure", Reviews of Modern Physics 72 (2000), 621-654
- C.A. Ashley and S. Doniach, "Theory of Extended X-ray Absorption Fine Structure (EXAFS) in Crystalline Solids", Physical Review B. 11, 1279-1288.
Problems
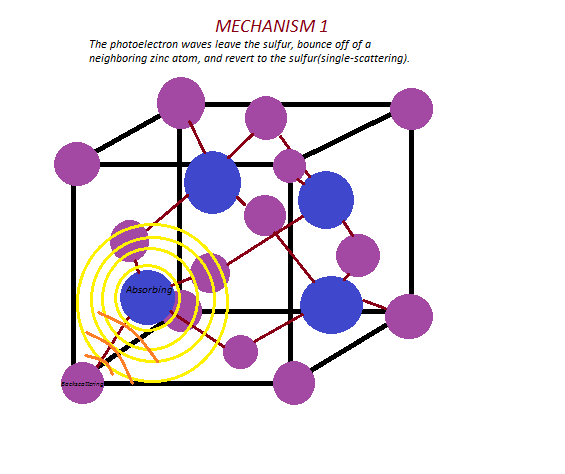
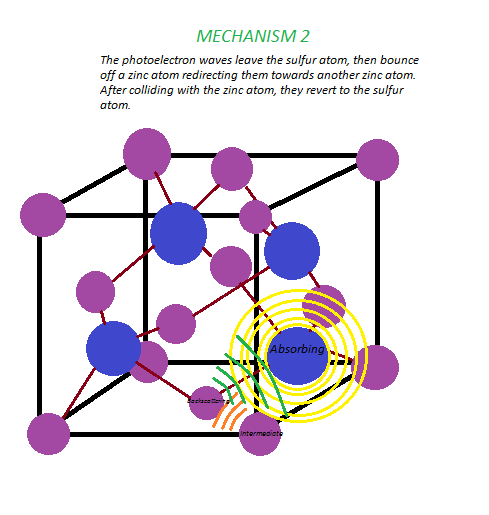
Consider the crystal lattice zinc sulfide, whose unit cell is pictured below.
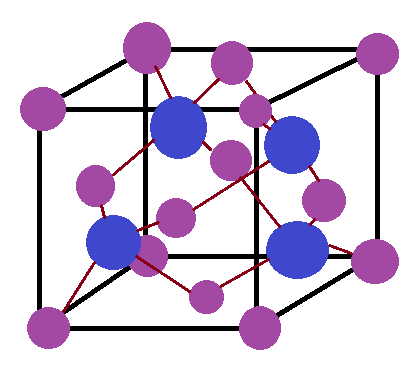
Zn = Purple, S = Blue.
- An X-Ray Beam is applied to a sample of ZnS, and excites a core sulfur electron. Sketch the raw spectrum you might expect to see, and indicate where the EXAFS/XANES regions may occur. Be sure to indicate where the K-edge is, and include units.
- For the phenomenon described, explain what happens to the energy associated with the ejection of the photoelectron?
- Upon completing data extraction, and transforming the final EXAFS equation into frequency space, describe what you would expect the radial distribution to look like for ZnS.
- How would the amplitude for the oscillations of a Zn connected to a single sulfur compare to the amplitude for the oscillations of a Zn from ZnS?
- When a photoelectron is emitted, spherical waves are produced. Redraw this unit cell, and sketch two possible paths these waves may take, taking into account nearest-neighbor atoms. Label the absorbing atom, backscattering atom, and intermediate atom, if applicable, in each diagram.
Answers
- Sulfur's K-edge occurs at about 2.472 keV(this can be found using online sources). If energy is plotted against the absorption coefficient, we would expect to see a constant flat line, then a sudden, sharp increase at roughly 2.472 keV. After this peak the spectrum would begin to decay, and there would be a few slight peaks(XANES), then steady downward oscillations(EXAFS).
- When the core sulfur electron is excited, this means the energy of the photon from the X-ray source exceeds the bonding energy of the electron. Its energy is consumed, and the electron becomes excited. This causes the ejection of the energy as a photoelectron wave.
- There would be expected to be a series of peaks, with four being prominent. These correspond to the four radial distances more likely to be occupied around the sulfur atom. Since in this unit cell each sulfur atom's coordination number is four, we would expect to see four main peaks, though in practice other peaks would probably interfere.
- Amplitude of backscattering is believed to be proportional to coordination number. Therefore, we would expect the amplitude of the oscillations to be about four times as high for this structure than for a single Zn-S bond.
5.