XANES - Theory II
- Page ID
- 1870
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)XANES, x-ray absorption near edge structure, is sometimes also called NEXAFS, near edge x-ray absorption fine structure. It is defined as partial analysis of x-ray absorption, and the range of XANES is between the threshold and where EXAFS begins. It can be used to determine the oxidation state and coordination number of the metal center in a complex; as well as the covalency and site symmetry of the molecule.
Introduction
XAS, x-ray abosorption spectroscopy, is a widely used technique for atomic local structure determination. A crystalline monochromator is usd to select the certain radiation with correspond energy that can excite a core electron. And there are mainly two region in the XAS spectrum, XANES and EXAFS.
The difference between XANES and EXAFS is loosely defined as space difference in terms of which regime they represent in a XAS spectrum. Apparently the conceptual principles of these two systems are technically the same, which is one of the limitations of this definition, because there is no clear principle definition to distinguish these two systems. In terms of energy level, people usually think the XANES is in the range where the potential is 50 eV above the edge; the EXAFS is in where the potential between 50 - 1000 eV above the edge.
Based on this, Bianconi also suggested that when a core electron gets excited at XANES, the wavelength of this photoelectron should be the distance between the absorbing atom and the closest atom/ligand.
Theory
During scanning, since the purpose is to excite a core electron, there will be no absorption until the energy of the radiation matches the ionization energy of the core electron. Then a hole will be left in the inner shell. A electron from higher energy state will fall into this vacancy, which cases releasing of energy. This released energy can either undergo a fluorescence emission to release a photon, or it can further excite and eject an electron from a higher energy state. This ejected electron is called auger electron.
Unlike traditional photoemission spectroscopy, in which the photoelectron is directly measured; however, in XANES, the intensities of the light come through samples are measured. Besides, the effect of scattering from auger electrons, photoelectrons, and even emitted photon are all included. In order to undstand how XANES works in the XAS and be able to extract useful information from it, learning how the scattering happens and works in the x-ray absorption is very important.
Absorption edge
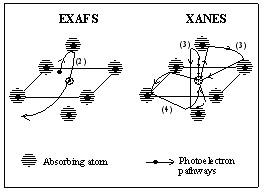
XANES in spectrum includes three portions: pre-edge, which is stroingly affected by bond lengths of molecules because of the exponentially decay of wavefunctions, edge, which is the big jump at 0 eV that indicate the ionization energy of core electrons, and XANES, which is the region from 0 to 50 eV above the threshold. As Figure 2 shows, the binding energy regime of a core shell is scanned by the radiation at certain frequency correspond to certain energy. There will be no absorption until the energy of the radiation matches the ionization energy of one core electron. There will be a big jump in the spectrum. What need to be notice here is that there is no selection rule for transition, because when the photon hit the core electron, it not only excites the electron, but also give kinetic energy to that electron to form a photoelectron. This photoelectron will be ejected and leave the atom. The most common edges are shown in Figure 1, K-edge (1s), L-edge (2s and 2p), M-edge (3s, 3p and 3d). These edges are corresponding to the priciple quantum number, n=1 (K-edge), n=2 (L-edge) and n=3 (M-edge), which indicate the order of electron shells. K, L and M are all x-ray notation.
Scattering
From the other perspective, the x-ray absorption spectroscopy can be used to determine the coordination number of a metal center and structure of a molecule based on how the scattering of photoelectrons or auger electrons affect the intensity of the radiation that come through the sample. When energy of the photon is high, in EXAFS, at continuum states which are high in energy, the atom can only have very weak effect on the system because the photoelectron that is ejected from the core orbitals is only weakly scattered by the surrounding atoms which are further from the absorbed atom. So all the electronic properties, or the interest in electron structure of the absorbed atom are centered on the low-lying extended states.
The theoretical analysis of the electron structure theory is to solve Schrödinger equation. Based on scattering theory, one can say that at high energy, EXAFS region, for the scattering of the photoelectron or auger electron are very weak, the main contribution of the scattering to the wave function of the final state is from the path that the excited electron is scattered only once. This process can be referred as single scattering. Since when the excited electron is scattering at one atom, there must be another scattering happening on the other atom on the opposite position, so the scattering in EXAFS can be treated as geometrical and the information is much easier to extract.
In the XANES region, when the energy is low, since neighboring atoms are not only close to the center atom, but also relatively close to each other, the excited electrons tend to bounce between the neighboring atoms before it hits back to the absorbed atom. So people call it multiple scattering in XANES regime compare to the single scattering in the EXAFS regime. The information details between the absorbing atoms and its neighbors, in terms of spatial arrangement, such as, radial distance, bond angles, and orientations relative to one another, are highly based on the multiple scattering. The multiple scattering expression is shown below,
\[\tau^{ij}_{LL'}=t^{i}_{l}\delta^{ij}\delta_{LL'}+t^{i}_{l}G^{ij}_{LL'}t^{j}_{l'}(1-\delta^{ij})+\sum_{k,L''}t^{i}_{l}G^{ik}_{LL''}t^{k}_{l''}G^{kj}_{L''L'}t^{j}_{l'}+\cdots\]
L stands for the pair of angular momentum quantum number. \(t^{i}_{l}\) is the l-wave t-matrix of atom i given in terms of the phase shift \(\delta^{i}_{l}\) by
\[t^{i}_{l}(\epsilon)=i/2k[e^{2i\delta^{i}_{l}}(\epsilon)-1]\]
and \(G^{ij}_{LL'}\) is a real space structure constant.
Each term in the expression represent an indvidual scattering path. This XANES cross-section is expressed as the sum of the sum of individual scattering path.
The scattering of excited electrons in XANES regime is very sensitive. Changing of charge distribution leads to changing of the chemical environment of the absorbed atom. And the absorption edge will shift in the XANES regime because the core-level energies are changed. Every molecule have their distinct charge distributions, and this is how one is able to figure out their structure and other spatial information based on XANES. However, there are a lot of physical effects evolved in the near-edge region, which may cause some problems when trying to extract specific information out of it.
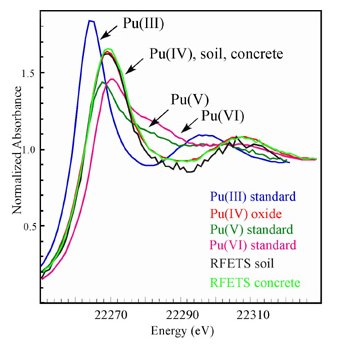
Figure 5. Illustration of different oxdation states provides different x-ray absorption spectra in XANES regime, which due to different chemical environment.-figure from Wikipedia
One-electron approximation
When there are more than one electron in a system,for example, in a hydrogen molecule, the interelectron term in the Hamiltonian is shown as below
\[H=-\frac{\hbar^{2}}{2m}\nabla^{2}_{1}-\frac{\hbar^{2}}{2m}\nabla^{2}_{2}-\frac{e^{2}}{4\pi\epsilon_{0}r_{a1}}-\frac{e^{2}}{4\pi\epsilon_{0}r_{a1}}-\frac{e^{2}}{4\pi\epsilon_{0}r_{b1}}-\frac{e^{2}}{4\pi\epsilon_{0}r_{b2}}+\frac{e^{2}}{4\pi\epsilon_{0}R}+\frac{e^{2}}{4\pi\epsilon_{0}r_{12}}\]
the last six terms, which are expression of potential energy of the four particles (two protons and two electrons) in the system, make impossibility to solve the Schrödinger equation. Then an approximation is made that instead of consider all these potential energy, the Haniltonian is expressed as the one electron which contains potential energy as the average of all the interactions.
\[f_{i}\phi_{i}=\epsilon_{i}\phi_{i}\]
where \(f_{i}\) is a sum of one-electron function, and \(\phi_{i}\) is a one-electron wavefunction.
This one-electron approximation, which is defined as the product of wave functions of many particles can be represented by a wave function of a single particle, is employed in the XANES theory. Even though density functional theory with local density approximation (LDA), which includes the exchange-correlation effect, can be used to figure out the electronic structure, it can be only applied in the ground state. In excited state, people need a quasiparticle description, and apparently one-electron state can give a pretty good approximation to the quasiparticle states. One thing about the one-electron eigenvalues in density functional theory is that instead of being the quasiparticle energies, they actually help the central object to obtain the correct total energy. From this, people know that excitation energy of local density approximationone-electron state cannot be determined, which, in XANES, means that LDA core eigenvalue can not accurately determine the core electron’s binding energy. However, the main spectra feature of interest in XANES regime is in the relative energy region above the threshold, instead of the threshold energy. So calculating the x-ray absorption spectra by using LDA one-electron eiganstate can give a pretty good approximation.
Advantages and Disadvantages
The most significant advantage of XANES, which also refers to as XAS, is that this technique is specific to elements. The signals in a XANES spectrum, llike fingerprints, represent only specific elements. Metal ions in molecules may be "silent" to some of spectroscopic techniques, such as EPR; however, XAS spectra can be taken of samples with a metal of interest, it provides detailed information about the oxidation state of the metal atoms. The sensitivity to multiple scattering makes it possible to extract three dimensional structure information from XANES spectra. Even though XANES can be used to determine local structure and many characteristics of atoms in a molecule, no technique is perfect. XANES also has its drawbacks. X-radiaiton can be destructive to samples, causing damage to the sample during the measurement process. In XAS spectra, espeically in XANES regime, oxidation state and the identity of scattering atom are difficult to determine because of the effect of mutiple scatterings by photoelectrons and auger electrons.
References
- Winefordner, L. D.(ED.) (1988). X-Ray Absorption. Chem. anal. 1988, 92, 53-83.
- Bianconi, A. Appl. Surf. Sci. 1980, 6, 392
Contributors and Attributions
- Shuai Wang

