4.3: Stability of Cycloalkanes - Ring Strain
- Page ID
- 31410
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After completing this section, you should be able to:
- Describe the Baeyer strain theory.
- Describe how the measurement of heats of combustion provides information about the amount of strain present in a cycloalkane ring.
- Determine the relative stability of cyclic compounds, by assessing such factors as angle strain, torsional strain and steric strain.
Make certain that you can define, and use in context, the key terms below.
- angle strain
- steric strain
- torsional strain
- ring strain
- heat of combustion
Heat of Combustion as a Measure of Bond Strength
The combustion of carbon compounds, especially hydrocarbons, has been the most important source of heat energy for human civilizations throughout recorded history. The practical importance of this reaction cannot be denied, but the massive and uncontrolled chemical changes that take place in combustion make it difficult to deduce mechanistic paths. Using the combustion of propane as an example, we see from the following equation that every covalent bond in the reactants has been broken and an entirely new set of covalent bonds have formed in the products. No other common reaction involves such a profound and pervasive change, and the mechanism of combustion is so complex that chemists are just beginning to explore and understand some of its elementary features.
\[\ce{CH_3CH_2CH_3 + 5O_2 -> 3CO_2 + 4H_2O + heat} \nonumber \]
Since all the covalent bonds in the reactant molecules are broken, the quantity of heat evolved in this reaction, and any other combustion reaction, is related to the strength of these bonds (and, of course, the strength of the bonds formed in the products). Precise heat of combustion measurements can provide useful information about the structure of molecules and their relative stability.
For example, heat of combustion is useful in determining the relative stability of isomers. Pentane has a heat of combustion of -782 kcal/mol, while that of its isomer, 2,2-dimethylpropane (neopentane), is –777 kcal/mol. These values indicate that 2,3-dimethylpentane is 5 kcal/mol more stable than pentane, since it has a lower heat of combustion.
Ring Strain
Table \(\PageIndex{1}\) lists the heat of combustion data for some simple cycloalkanes. These cycloalkanes do not have the same molecular formula, so the heat of combustion per each CH2 unit present in each molecule is calculated (the fourth column) to provide a useful comparison. From the data, cyclopropane and cyclobutane have significantly higher heats of combustion per CH2, while cyclohexane has the lowest heat of combustion. This indicates that cyclohexane is more stable than cyclopropane and cyclobutane, and in fact, that cyclohexane has a same relative stability as long chain alkanes that are not cyclic. This difference in stability is seen in nature where six membered rings are by far the most common. What causes the difference in stability or the strain in small cycloalkanes?
| Cycloalkane (CH2)n |
CH2 Units n |
ΔH25º kcal/mol |
ΔH25º per CH2 Unit |
Ring Strain kcal/mol |
|---|---|---|---|---|
| Cyclopropane | n = 3 | 468.7 | 156.2 | 27.6 |
| Cyclobutane | n = 4 | 614.3 | 153.6 | 26.4 |
| Cyclopentane | n = 5 | 741.5 | 148.3 | 6.5 |
| Cyclohexane | n = 6 | 882.1 | 147.0 | 0.0 |
| Cycloheptane | n = 7 | 1035.4 | 147.9 | 6.3 |
| Cyclooctane | n = 8 | 1186.0 | 148.2 | 9.6 |
| Cyclononane | n = 9 | 1335.0 | 148.3 | 11.7 |
| Cyclodecane | n = 10 | 1481 | 148.1 | 11.0 |
| CH3(CH2)mCH3 | m = large | — | 147.0 | 0.0 |
The Baeyer Theory on the Strain in Cycloalkane Rings
In 1890, the famous German organic chemist, A. Baeyer, suggested that cyclopropane and cyclobutane are less stable than cyclohexane, because the the smaller rings are more "strained". There are many different types of strain that contribute to the overall ring strain in cycloalkanes, including angle strain, torsional strain, and steric strain. Torsional strain and steric strain were previously defined in the discussion of conformations of butane. Angle Strain occurs when the sp3 hybridized carbons in cycloalkanes do not have the expected ideal bond angle of 109.5o, causing an increase in the potential energy. An example of angle strain can be seen in the diagram of cyclopropane below in which the bond angle is 60o between the carbons. The compressed bond angles causes poor overlap of the hybrid orbitals forming the carbon-carbon sigma bonds which in turn creates destabilization.
The C-C-C bond angles in cyclopropane (diagram above) (60o) and cyclobutane (90o) are much different than the ideal bond angle of 109.5o. This bond angle causes cyclopropane and cyclobutane to be less stable than molecules such as cyclohexane and cyclopentane, which have a much lower ring strain because the bond angle between the carbons is much closer to 109.5o. Changes in chemical reactivity as a consequence of angle strain are dramatic in the case of cyclopropane, and are also evident for cyclobutane.
In addition to angle strain, there is also steric (transannular) strain and torsional strain in many cycloalkanes. Transannular strain exists when there is steric repulsion between atoms.
Because cycloalkane lack the ability to freely rotate, torsional (eclipsing) strain exists when a cycloalkane is unable to adopt a staggered conformation around a C-C bond. Torsional strain is especially prevalent in small cycloalkanes, such as cyclopropane, whose structures are nearly planar.
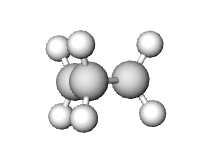
The Eclipsed C-H Bonds in Cyclopropane
Larger rings like cyclohexane, deal with torsional strain by forming conformers in which the rings are not planar. A conformer is a stereoisomer in which molecules of the same connectivity and formula exist as different isomers, in this case, to reduce ring strain. The ring strain is reduced in conformers due to the rotations around the sigma bonds, which decreases the angle and torsional strain in the ring. The non-planar structures of cyclohexane are very stable compared to cyclopropane and cyclobutane, and will be discussed in more detail in the next section.
- Angle Strain - The strain caused by the increase or reduction of bond angles
- Torsional Strain - The strain caused by eclipsing bonds on adjacent atoms
- Steric Strain - The strain caused by the repulsive interactions of atoms trying to occupy the same space
trans-1,2-Dimethylcyclobutane is more stable than cis-1,2-dimethylcyclobutane. Explain this observation.
- Answer
-
The trans form does not have eclipsing methyl groups, therefore lowering the energy within the molecule. It does however have hydrogen-methyl eclipsing interactions which are not as high in energy as methyl-methyl interactions.
Cyclobutane has more torsional stain than cyclopropane. Explain this observation.
- Answer
-
Cyclobutane has 4 CH2 groups while cyclopropane only has 3. More CH2 groups means cyclobutane has more eclipsing H-H interactions and therefore has more torsional strain.
Exercises
- Trans-1,2-Dimethylcyclobutane is more stable than cis-1,2-dimethylcyclobutane. Explain this observation.
- The trans form does not have eclipsing methyl groups, therefore lowering the energy within the molecule. It does however have hydrogen-methyl interactions, but are not as high in energy than methyl-methyl interactions.

