22.5: Effect of Substituents on Reactivity and Orientation in Electrophilic Aromatic Substitution
- Page ID
- 22327
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In planning syntheses based on substitution reactions of substituted benzenes, it is imperative to be able to predict in advance which of the available positions of the ring are likely to be most reactive. This is now possible with a rather high degree of certainty, thanks to the work of many chemists during the past 100 years. Few, if any, other problems in organic chemistry have received so much attention over so many years, and there are now sufficient data on the orientation and reactivity effects of ring substituents in electrophilic substitution to permit the formation of some very valuable generalizations.
Basically, three experimental problems are involved in the substitution reactions of aromatic compounds: (1) proof of structure of the isomers that are formed; (2) determination of the percentage of each isomer formed, if the product is a mixture; and (3) measurement of the reactivity of the compound being substituted relative to some standard substance, usually benzene.
For benzenoid compounds, structures can be established by the historically important substitution method (Section 1-1F) or with the aid of correlations between spectroscopic properties and positions of substitution, as we indicated in Section 22-3. Also, it is often possible to identify the isomers by converting them to compounds of known structure. For example, trifluoromethylbenzene on nitration gives only one product, which has been shown to be the 3-nitro derivative by conversion to the known 3-nitrobenzoic acid by concentrated sulfuric acid:
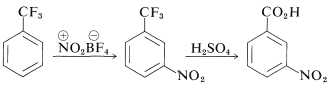
The ratios of isomers formed in substitution reactions can be determined by spectroscopic means or by the analytical separation methods discussed in Section 9-2. We mainly are concerned in this chapter with the reactivity and orientation observed in aromatic substitution.
The Pattern of Orientation in Aromatic Substitution
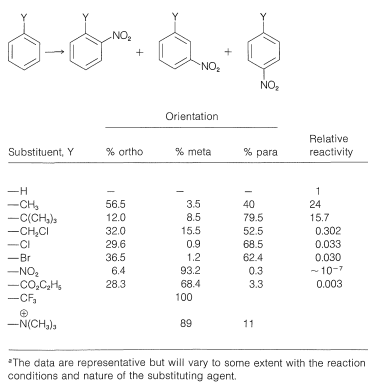
The reaction most studied in connection with the orientation problem is nitration, but the principles established also apply for the most part to the related reactions of halogenation, sulfonation, alkylation, and acylation. Some illustrative data for the nitration of a number of mono-substituted benzene derivatives are given in Table 22-5. The table includes the percentage of ortho, meta, and para isomers formed, along with their reactivities relative to benzene. We see that there is a wide range of reactivity according to the nature of the substituent, and that the ortho, meta, and para positions are not equally reactive. Although these substituent effects may appear complex, they are related closely to substituted alkenes (Section 10-4), as will be explained in the following section.
Table 22-5: Orientation and Rate Data for Nitration of Some Monosubstituted Benzene Derivatives\(^a\)
Electronic Effects
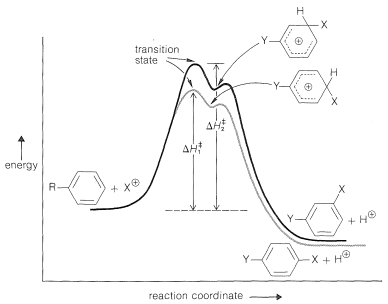
It is helpful to construct an energy diagram for substitution by an electrophilic \(\ce{X}^\oplus\) of a benzene derivative, \(\ce{C_6H_5Y}\), in which \(\ce{Y}\) is a substituent group (Figure 22-8). The rate of substitution at any one position (we have arbitrarily chosen in Figure 22-8 to compare the 3 and 4 positions) will depend on the height of the energy barrier between the reactants and the transition state. Effects that act to lower the heights of the barriers increase the rates of substitution. Because the transition state and the positively charged intermediate for aromatic substitution have much the same energy, any effect that stabilizes this intermediate is likely to lower the energy of the transition state and increase the rate of substitution. Thus under conditions of kinetic control the preferred arene substitution product, as in alkene addition, will be that derived from the most stable of the possible intermediates. Therefore the problem of predicting relative rates and orientation in aromatic substitution becomes one of deciding what factors are likely to stabilize or destabilize the various possible intermediates relative to one another and to the ground state.
We now can examine the structures of the three substitution intermediates with a view to deciding how the substituent might affect their stability. According to the valence-bond method, the positive charge in the ring is dispersed mainly on alternate carbons, as shown below.
ortho substitution
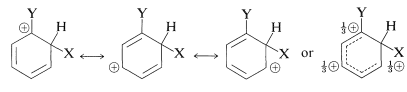
para substitution
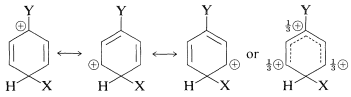
meta substitution
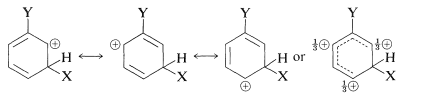
The substituent \(\ce{Y}\) should (and does) exert its electronic influence more strongly from the ortho and para positions than from the meta position because \(\ce{Y}\) in the ortho and the para positions is close to a positively charged ring carbon. This electronic influence will be stabilizing if \(\ce{Y}\) has a net electron-donating effect, and destabilizing if \(\ce{Y}\) is electron withdrawing. A group can withdraw electrons relative to hydrogen if it is more electronegative than hydrogen and this is called the electron-withdrawing inductive effect (also see Section 18-2B). A group also can withdraw electrons by the resonance effect:
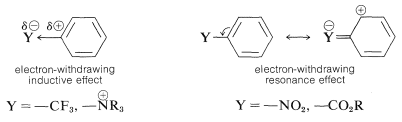
Accordingly, substituents fall into one of the following categories.
Meta-directing substituents
A ring substituent \(\ce{Y}\) that is electron withdrawing relative to hydrogen and has no capacity to donate electrons by a resonance effect will decrease the reactivity of \(\ce{C_6H_5Y}\), especially at the ortho and para positions. The result is a sluggish reaction (deactivation) with substitution occurring preferentially at the meta position. Substituents in this category are \(\ce{-NO_2}\), \(\ce{-CF_3}\), \(\ce{-CO_2R}\), \(\ce{-} \overset{\oplus}{\ce{N}} \ce{R_3}\), and so on (also see Tables 22-5 and 22-6). No groups are known that direct the electrophile to the meta position and, at the same time, make the phenyl derivative more reactive relative to benzene.
Table 22-6: Orientation and Reactivity Effects of Ring Substituents
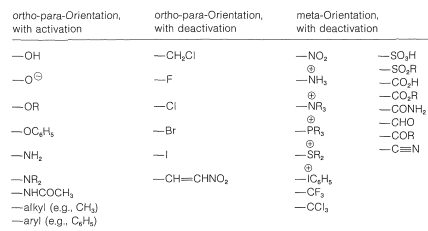
Ortho-para directing substituents
1. A ring substituent, \(\ce{-Y}\), that has an electron pair on the atom adjacent to the ring gives ortho-para substitution in preference to meta substitution. The reason is that the intermediate can be stabilized by an electron-donating resonance effect from \(\ce{Y}\) that is effective from the ortho and para positions only:
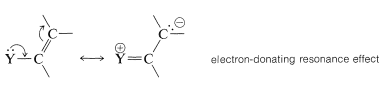
This effect is made clear in the valence-bond structures for the ortho-para substitution intermediates from benzenol (phenol):
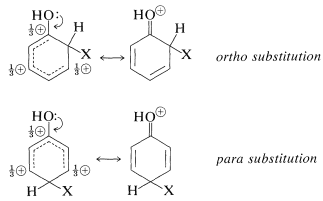
Substituents of the type \(\ce{-Y}\) include \(\ce{-OH}\), \(\ce{-OR}\), \(\ce{-SR}\), \(\ce{-NH_2}\), and halogens. Most of these groups also are electron withdrawing by an inductive effect that opposes their resonance effect. However, as we saw in the case of alkene additions (Section 10-4C), even when \(\ce{-Y}\) is an electronegative group, stabilization of the intermediate cation by donation of unshared electrions of \(\ce{Y}\) to the adjacent positive carbon more than compensates for the polar electron-withdrawing properties of \(\ce{Y}\). Electron donation thus controls the orientation. If, however, the group is strongly electron withdrawing (e.g., \(\ce{-Y} = \ce{-F}\), \(\ce{-Cl}\), \(\ce{-Br}\), \(\ce{-I}\)), the reactivity of the compound \(\ce{C_6H_5Y}\) may be reduced. Groups of this kind are ortho-para directing with deactivation.
But if the polar effect is not pronounced, then substitution can be powerfully assisted by the substituent. This is ortho-para direction with activation and is provided by groups such as \(\ce{-OH}\), \(\ce{-OR}\), \(\ce{-SR}\), and \(\ce{-NH_2}\). A more comprehensive list of substituents and their orientation effects is provided in Table 22-6.
2. When no important \(\pi\)-electron effect is possible, as with alkyl groups, the orientation effect of a substituent is controlled by its polar effect and the degree to which it polarizes the bonding electrons of the ring. Alkyl groups actually are electron donating and therefore are ortho-para directing with activation.

Steric Effects
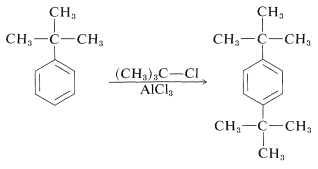
Thus far we have made no distinction between the reactivities of the ortho and the para positions, yet they clearly are not equal. If they were equal, the ortho:para ratio would be 2:1, thereby reflecting the fact that there are two ortho positions but only one para position in monosubstituted benzenes. Most substitution reactions favor the para product, sometimes by a considerable amount (see Table 22-5). A reasonable explanation is that ortho substitution is subject to steric hindrance between the substituent and the entering group. tert-Butylbenzene, for example, gives much less ortho nitration than methylbenzene (Table 22-5), thereby suggesting that the size of the substituent is important. Also, tert-butylbenzene gives no ortho alkylation with tert-butyl chloride, suggesting that the size of the entering group is also important:
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


