10.5: Orientation in Addition to Alkenes
- Page ID
- 22247
Addition of \(\ce{HX}\)
Addition of an unsymmetrical substance such as \(\ce{HX}\) to an unsymmetrical alkene theoretically can give two products:
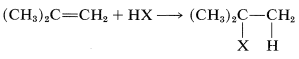 and
and 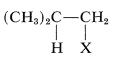
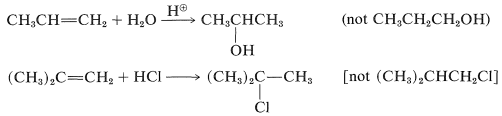
Both products are seldom formed in equal amounts; in fact, one isomer usually is formed to the exclusion of the other. For example, the hydration of propene gives 2-propanol (not 1-propanol), and hydrogen chloride adds to 2-methylpropene to give tert-butyl chloride (not isobutyl chloride):
To understand the reason for the pronounced selectivity in the orientation of addition of electrophiles, it will help to consider one example, hydrogen bromide addition to 2-methylpropene. Two different carbocation intermediates could be formed by attachment of a proton to one or the other of the double bond carbons:
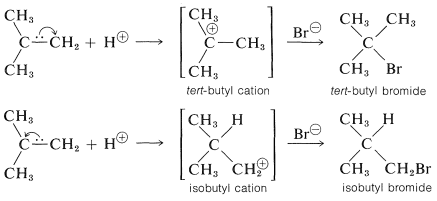
Subsequent reactions of the cations with bromide ion give tert-butyl bromide and isobutyl bromide. In the usual way of running these additions, the product is very pure tert-butyl bromide.
How could be have predicted which product would be favored? The first step is to decide whether the prediction is to be based on (1) which of the two products is the more stable, or (2) which of the two products if formed more rapidly. If we make a decision on the basis of product stabilities, we take into account \(\Delta H^0\) values, entropy effects, and so on, to estimate the equilibrium constants \(K_\text{eq}\) for the reactants and each product. When the ratio of the products is determined by the ratio of their equilibrium constants, we say the overall reaction is subject to equilibrium (or thermodynamic) control. Equilibrium control requires that the reaction be reversible.
When a reaction is carried out under conditions in which it is not reversible, the ratio of the products is determined by the relative rates of formation of the various products. Such reactions are said to be under kinetic control.
The products obtained in a reaction subject to kinetic control are not necessarily the same as those obtained under equilibrium control. Indeed, the equilibrium constant for interconversion of tert-butyl bromide and isobutyl bromide at \(25^\text{o}\) is 4.5, and if the addition of hydrogen bromide to 2-methylpropene were under equilibrium control, the products would be formed in this ratio:
\[K_\text{eq} = \dfrac{\left[ \text{tert-butyl bromide} \right]}{\left[ \text{isobutyl bromide} \right]} = 4.5\]
But the addition product is \(99+\%\) tert-butyl bromide so the reaction clearly is kinetically controlled, tert-butyl being formed considerably faster than isobutyl bromide. The slow, or rate-determining, step in this reaction is the formation of the intermediate cation rather than the reaction of the cation with bromide ion. So to account for the formation of tert-butyl bromide we have to consider why the tert-butyl cation is formed more rapidly than the isobutyl cation:
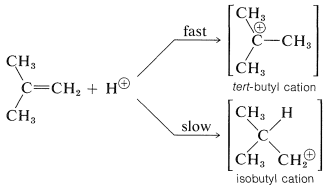
As we have seen in Section 8-7B, alkyl groups are more electron donating than hydrogen. This means that the more alkyl groups there are on the positive carbon of the cation, the more stable and the more easily formed the cation will be. The reason is that electron-donating groups can partially compensate for the electron deficiency of the positive carbon. As a result, we can predict that the tert-butyl cation with three alkyl groups attached to the positive center will be formed more readily than the primary isobutyl cation with one alkyl group attached to the positive center.
Thus the problem of predicting which of the two possible products will be favored in the addition of unsymmetrical reagents to alkenes under kinetic control reduces to predicting which of two possible carbocation intermediates will be formed most readily. With simple alkenes, we shall expect the preference of formation of the carbocations to be in the order:
tertiary > secondary > primary.
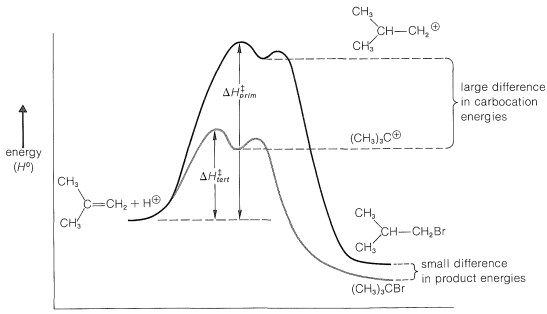
The reaction scheme can be represented conveniently in the form of an energy diagram (Figure 10-10). The activation energy, \(\Delta H^1_\text{tert}\) for the formation of the tert-butyl cation is less than \(\Delta H^1_\text{prim}\) for the formation of the isobutyl cation because the tertiary ion is much more stable (relative to the reactants) than the primary ion, and therefore is formed at the faster rate. The second step, to form the product from the intermediate cation, is very rapid and requires little activation energy. Provided that the reaction is irreversible, it will take the lowest-energy path and form exclusively tert-butyl bromide. However, if the reaction mixture is allowed to stand for a long time, isobutyl bromide begins to form. Over a long period, the products equilibrate and, at equilibrium, the product distribution reflects the relative stabilities of the products rather than the stability of the transition states for formation of the intermediates.
A rather simple rule, formulated in 1870 and known as Markownikoff's rule, correlates the direction of kinetically controlled additions of \(\ce{HX}\) to unsymmetrical alkenes. This rule, an important early generalization of organic reactions, may be stated as follows: In addition of \(\ce{HX}\) to an unsymmetrical carbon-carbon double bond, the hydrogen of \(\ce{HX}\) goes to that carbon of the double bond that carries the greater number of hydrogens. It should be clear that Markownikoff's rule predicts that addition of hydrogen bromide to 2-methylpropene will give tert-butyl bromide.
Addition of Other Reagents to Unsymmetrical Alkenes. The Electronegativity Chart
We can extend Markownikoff's rule to cover additions of substances of the general type \(\ce{X-Y}\) to unsymmetrically substituted alkenes when a clear-cut decision is possible as to whether \(\ce{X}\) or \(\ce{Y}\) is the more electrophilic atom of \(\ce{X-Y}\). If the polarization of the \(\ce{X-Y}\) bond is such that \(\ce{X}\) is positive, \(^{\delta \oplus} \ce{X-Y} ^{\delta \ominus}\), then \(\ce{X}\) will be expected to add as \(\ce{X}^\oplus\) to the alkene to form the more stable carbocation. This step will determine the direction of addition. For example, if we know that the \(\ce{O-Br}\) bond of \(\ce{HOBr}\) is polarized as \(\overset{\delta \ominus}{\ce{HO}} - \overset{\delta \oplus}{\ce{Br}}\), then we can predict that addition of \(\ce{HOBr}\) to 2-methylpropene will give 1-bromo-2-methyl-2-propanol:

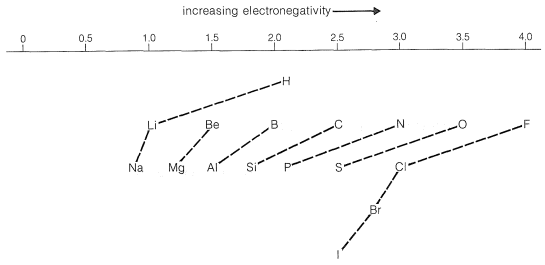
Pauling's value for the electronegativity of carbon makes it slightly more electron-attracting than hydrogen. However, we expect that the electron-attracting power of a carbon atom (or of other elements) will depend also on the electronegativities of the groups to which it is attached. In fact, many experimental observations indicate that carbon in methyl or other alkyl groups is significantly less electron-attracting than hydrogen. Conversely, the \(\ce{CF_3}-\) group is, as expected, far more electron-attracting than hydrogen.
The direction of polarization of bonds between various elements may be predicted from Figure 10-11. For example, an \(\ce{O-Cl}\) bond should be polarized so the oxygen is negative; a \(\ce{C-N}\) bond should be polarized so the nitrogen is negative:
\[\overset{\delta \ominus}{\ce{O}}---\overset{\delta \oplus}{\ce{Cl}} \: \: \: \: \: \overset{\delta \oplus}{\ce{C}}---\overset{\delta \ominus}{\ce{N}}\]
We then can predict that, in the addition of \(\ce{HOCl}\) to an alkene, the chlorine will add preferentially to form the more stable of two possible carbon cations. Generally, this means that chlorine will bond to the carbon carrying the greater number of hydrogens:
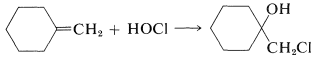
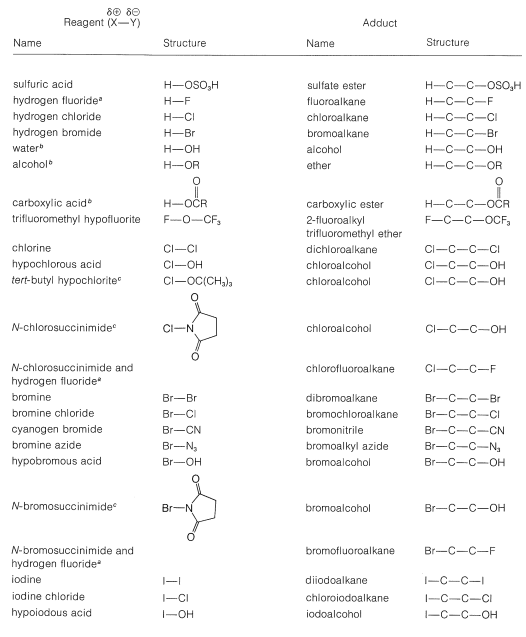
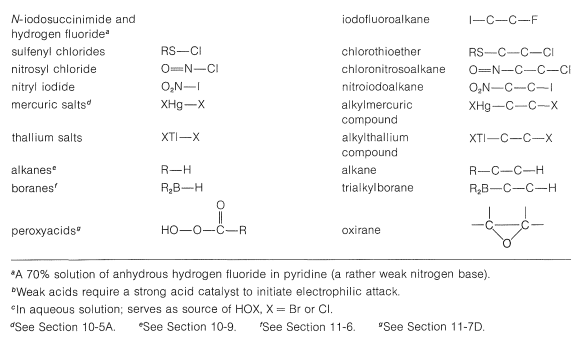
A number of reagents that are useful sources of electrophilic halogen are included in Table 10-2. Some of these reagents, notably those with \(\ce{O}-\)halogen or \(\ce{N}-\)halogen bonds, actually are sources of hypohalous acids, \(\ce{HOX}\), and function to introduce halogen and hydroxyl groups at carbon. There are very few good fluorinating agents whereby the fluorine is added as \(\ce{F}^\oplus\).
Table 10-2: Reagents that add to Alkenes by Electrophilic Attack:
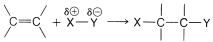
Additions to Substituted Alkenes
For alkenes that have halogen or similar substituents at the doubly bonded carbons, the same principles apply as with the simple alkenes. That is, under kinetic control the preferred product will be the one derived from the more stable of the two possible intermediate carbon cations. Consider a compound of the type \(\ce{Y-CH=CH_2}\). If \(\ce{Y}\) is more electron-attracting than hydrogen, then hydrogen halide should add in such a way as to put the proton of \(\ce{HX}\) on the \(\ce{YCH=}\) end and \(\ce{X}\) on the \(\ce{=CH_2}\) end. The reason is that the positive carbon is expected to be more favorably located if it is not attached directly to an electron-attracting substituent:

The addition goes as predicted, provided that the atom directly attached to the carbon of the double bond carries no unshared (nonbonding) electron pairs. For example,
\[\ce{CF_3-CH=CH_2} + \ce{HCl} \rightarrow \ce{CF_3-CH_2-H_2-Cl}\]
Such substituents are relatively uncommon, and most of the reported \(\ce{H-X}\) additions have been carried out with \(\ce{Y}\) groups having unshared electron pairs on an atom connected directly to a carbon of the double bond:
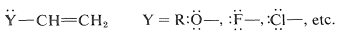
These substituents usually are strongly electronegative relative to hydrogen, and this often causes diminished reactivity of the double bond toward electrophiles. Nonetheless, the preferred orientation of \(\ce{HX}\) additions situates the positive charge of the intermediate carbocation next to the substituent:
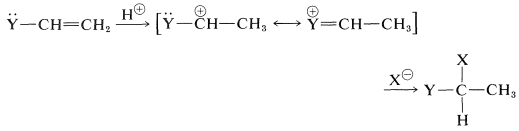
The electron-attracting power of the substituent is more than counterbalanced by stabilization of the intermediate cation by the ability of the substituents to delocalize their unshared electrons to the adjacent positive carbon (see Section 6-6).
References
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


