18.3: Some Chemical Properties of Carboxylic Acids
- Page ID
- 22288
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Most of the reactions of carboxylic acids belong to one of four principal classes, depending on the point in the molecule where the reaction occurs.
a. Reactions involving the \(\ce{O-H}\) bond - these include acid dissociation and solvolytic reactions.
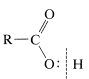
b. Reactions at the carbonyl bond - most of which involve attack by a nucleophile \(: \ce{Nu}\) on the carbonyl carbon with subsequent cleavage of a \(\ce{C-O}\) bond. Examples are esterification, acyl chloride formation, and reduction with hydrides.

c. Decarboxylation - these are reactions in which the \(\ce{R-C}\) bond is broken in such a way that \(\ce{CO_2}\) is lost and \(\ce{R-H}\) is formed.
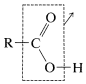
d. Substitution on the \(\ce{R}\) group - substitutions for hydrogen or halogen at the 2-carbon are especially important.
We will emphasize the way in which the chemistry of carboxylic acids in each of these categories can be correlated with the principles outlined in previous chapters.
Dissociation of Carboxylic Acids. The Resonance Effect
Compared with mineral acids such as hydrochloric, perchloric, nitric, and sulfuric acids, the carboxylic acids, \(\ce{CH_3(CH_2)}_n \ce{CO_2H}\), are weak. The extent of dissociation in aqueous solution is relatively small, the acidity constants, \(K_\text{a}\), being approximately \(10^{-5}\) (see Table 18-1).
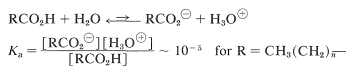
Even though the carboxylic acids are weak acids, they are many orders of magnitude stronger than the corresponding alcohols, \(\ce{CH_3(CH_2)}_n \ce{CH_2OH}\). Thus the \(K_\text{a}\) of ethanoic acid, \(\ce{CH_2CO_2H}\), is \(10^{11}\) times larger than that of ethanol, \(\ce{CH_3CH_2OH}\).
The acidity of the carboxyl group arises, at least in part, from the polar nature of the carbonyl group, the polarity of which can be ascribed to contributions of the structure
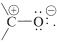
For a carboxyl group, these structures and an additional possibility are shown by \(1a\), \(1b\), and \(1c\):
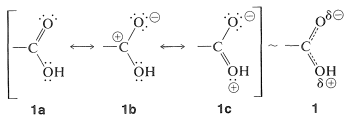
Although the uncharged structure, \(1a\), is of major importance, structures \(1b\) and \(1c\) make significant contributions. The stabilization is substantial and carboxylic acids are more stable than would be expected, from summing up their bond energies, by fully \(18 \: \text{kcal mol}^{-1}\).
The stabilization energy of the carboxylate anion is substantially greater than that of the acid, because the anion is a resonance hybrid of two energetically equivalent structures, \(2a\) and \(2b\), whereas the acid is represented by a hybrid of nonequivalent structures, \(1a\) through \(1c\):

The rules for resonance stress that the greatest stabilization is expected when the contributing structures are equivalent (Section 6-5B). Therefore we can conclude that the resonance energy of a carboxylate anion should be greater than that of the corresponding acid. Consequently we can say that there is a "driving force" (a gain in stability) that promotes the dissociation of carboxylic acids. The fact that alcohols are far weaker acids than carboxylic acids may be attributed to the lack of stabilization of alkoxide ions compared to that of carboxylate anions. The difference in energy corresponding to the dissociation of a carboxylic acid (Equation 18-1) relative to that of an alcohol (Equation 18-2) actually amounts to about \(15 \: \text{kcal mol}^{-1}\):

The Inductive Effect and Acid Strengths
You may have noticed that there are considerable differences between the strengths of some of the acids listed in Table 18-1. Methanoic acid and almost all the substituted ethanoic acids are stronger than ethanoic acid. In fact, trifluoroethanoic acid is similar in strength to hydrochloric acid. The substituent groups clearly can have a profound effect on acid strength by what commonly is called the inductive effect, an effect related to the electronegativity of the substituent. The inductive effect is different from resonance effects discussed in Section 18-2A in that it is associated with substitution on the saturated carbon atoms of the chain. The inductive effect of the substituent makes the acid stronger or weaker (relative to the unsubstituted acid), depending on whether the substituent is electron-attracting or electron-donating relative to hydrogen.
The electronegativity scale (Section 10-4B) shows chlorine to be more electron-attracting than hydrogen, and chloroethanoic acid is an 80-times stronger acid than ethanoic acid itself. Substitution by more chlorines enhances the acidity. Dichloroethanoic acid is 3000 times and trichloroethanoic acid is 5000 times more acidic than ethanoic acid. Moving the position of substitution along the chain away from the carboxyl group makes the effect smaller, and 4-chlorobutanoic acid is only a two-times stronger acid than butanoic acid (Table 18-1).
The inductive effect of the substituent can be considered to be transmitted to the carboxyl group in two rather different ways. Most frequently, the substituent is regarded as causing shifts in the average distributions of the bonding electrons along the chain of atoms between it and the carboxyl proton. This produces a succession of electron shifts along the chain, which, for an electron-attracting substituent, increases the acid strength by making it more energetically feasible for the \(\ce{-OH}\) hydrogen of the carboxyl group to leave as a proton:
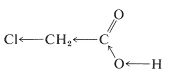
Many other groups besides halogens exhibit electron-withdrawing acid-enhancing inductive effects. Among these are nitro \(\left( \ce{-NO_2} \right)\), methoxy \(\left( \ce{CH_3O} \right)\), carbonyl (\(\ce{RCOR'}\), as in aldehydes, ketones, acids, esters, and amides), cyano or nitrile \(\left( \ce{-C \equiv N} \right)\), and trialkylammonium \(\left( \ce{R_3} \overset{\oplus}{\ce{N}} \ce{-} \right)\). Alkyl groups - methyl, ethyl, isopropyl, and so on - are the only substitutents listed in Table 18-1 that are acid-weakening relative to hydrogen (as can be seen by comparing the \(K_\text{a}\) values of the longer-chain acids with those of methanoic and ethanoic acids). We may take this to mean that alkyl groups release electrons to the carboxyl group.
The Electrostatic Interpretation of Acid Strengths
The other possible mode of transmission of the polar effect of a substituent group is a purely electrostatic one, sometimes called the "field effect", in which the dipole of the substituent produces an electrostatic field at the carboxyl proton, which helps or hinders ionization depending on the way in which the dipole is oriented with respect to the carboxyl group. It is easiest to visualize how the electrostatic theory operates by considering a proton midway between two well-separated carboxylate anions and deciding with which one the proton can combine more favorably. The more favorable one will correspond to the more basic carboxylate anion and the weaker carboxylic acid. With \(\ce{CH_3CO_2^-}\) and \(\ce{ClCH_2CO_2^-}\) as examples, and remembering that the \(\ce{Cl-C}\) bond is polarized as \(\overset{\delta \ominus}{\ce{Cl}} \ce{-} \overset{\delta \oplus}{\ce{C}}\), we can write:

The proton will be attracted by both \(\ce{-CO_2^-}\) groups and the differences in electrostatic energy of its combination with one or the other of the carboxylate groups will depend on the influence of the \(\overset{\delta \ominus}{\ce{Cl}} \ce{-} \overset{\delta \oplus}{\ce{C}} \ce{H_2}\) dipole. The \(\overset{\delta \ominus}{\ce{Cl}}\) end of the dipole will attract the proton, but the \(\overset{\delta \oplus}{\ce{C}} \ce{H_2}\) end will repel it. The repulsion effect will be more important because the \(\overset{\delta \oplus}{\ce{C}} \ce{H_2}\) is closer than \(\overset{\delta \ominus}{\ce{Cl}}\) to the final point of attachment of the proton to the carboxylate oxygen.\(^2\) Thus, the proton will go more favorably to \(\ce{CH_3CO_2^-}\) than to \(\ce{ClCH_2CO_2^-}\), which means that \(\ce{ClCH_2CO_2H}\) is a stronger acid than \(\ce{CH_3CO_2H}\).
Quantitative application of electrostatic theory to the effect of substituents on the ionization of carboxylic acids, such as chloroethanoic acid, is rendered difficult by the fact that the polarized \(\overset{\delta \ominus}{\ce{Cl}} \ce{-} \overset{\delta \oplus}{\ce{C}} \ce{H_2}\) bond and the proton cannot be treated as if they were point charges in a vacuum. The intervening and surrounding matter must be taken into account. This is especially true for water solutions because a molecule of an organic acid in water is a cavity of low dielectric constant immersed in a medium of high dielectric constant. Therefore, when ionization occurs the proton goes from inside the cavity through the boundary into the water. At the same time, the nature of the cavity must change because it then contains an anion, not a neutral molecule.
What Part Does Entropy Play in the Dissociation of Carboxylic Acids?
We have discussed the influence of substituents on acid strengths of simple carboxylic acids as though the full electrostatic effect of the substituent were exerted solely on the \(\Delta H\) of ionization. However, careful thermodynamic analysis of acidities in aqueous solution show that entropy effects (Section 4-4B) are very important. This may seem surprising because entropy effects ought to be small for relative acid strengths, which can be assessed by the constants for simple equilibria such as Equation 18-3, in which (1) there are the same number of molecules on each side of the equation, and (2) the constraints on the species involved hardly seem different from one side of the equation to the other:
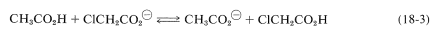
The entropy effects associated with these equilibria have to do with the "invisible" participant, water, which is involved in an intimate way, although by convention we omit it from equations such as 18-3. Solvation of ions puts constraints on water molecules, and the same electrostatic effects that change the ease of removing the proton act to change the degree and nature of solvation, thereby requiring consideration of entropy effects on the equilibria.
If solvation entropy effects are important, how can we justify using simple electrostatic theory to account for changes in acid strengths produced by substituents? The answer lies in \(\Delta G\); whatever the electrostatic effects are doing to balance between \(\Delta H\) and \(\Delta S\), it is \(\Delta G\) that determines the equilibrium constant and \(\Delta G\) quite consistently follows the predictions of simple electrostatic considerations. Furthermore, the relative acid strengths of a number of substituted ethanoic acids have been determined in the gas phase by ion-cyclotron resonance (Section 27-8), under conditions where association and solvent effects are absent (Section 11-8A). In the gas phase, entropy effects are small and the relative acidities are in the order expected from the electronegativity scale, provided on corrects for the ion-size effect that we encountered previously with respect to the gas-phase acidities of alkynes and alcohols (Section 11-8B and 15-4A). Thus fluoroethanoic acid is weaker than chloroethanoic acid in the gas phase, whereas the reverse is true in water solution. The difference may be due simply to the fact that larger ions are in general more stable than smaller ions in the gas phase.
Carboxylic Acids as Bases
In addition to their acidic properties, carboxylic acids also can act as weak bases when the carbonyl oxygen accepts a proton from a strong acid, such as \(\ce{H_2SO_4}\), \(\ce{HClO_4}\), or \(\ce{HSbF_6}\) in \(\ce{SO_2}\) (Equation 18-4). Such protonation is an important step in acid-catalyzed esterification, as discussed in Section 15-4D:
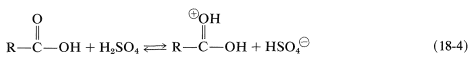
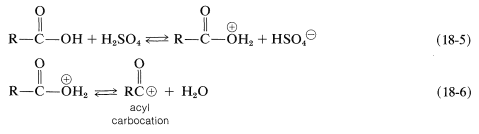
A proton also can add to the hydroxyl oxygen (Equation 18-5). The resulting conjugate acid normally is less favorable than its isomer with the proton on the carbonyl group. Nonetheless, this conjugate acid plays a role in esterification when the \(\ce{R}\) group is particularly bulky and, in addition, has electron-donating properties, thereby favoring ionization to an acyl carbocation (as in Equation 18-6; see also Section 18-3A):
Salts of Carboxylic Acids as Soaps. Micelle Formation
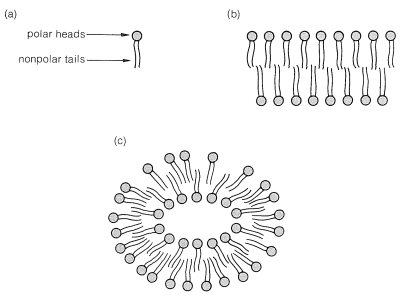
Carboxylic acids have an important practical use in the form of their metal salts as soaps. We have mentioned how fats, which are 1,2,3-propanetriol (glyceryl) esters of long-chain acids, can be hydrolyzed with alkali to give the corresponding carboxylate salts. It has been known as far back as Roman times (Pliny) that such substances have value for cleaning purposes.\(^3\) These salts have a complicated interaction with water because they are very polar at the salt end of the molecule and very nonpolar at the long-chain hydrocarbon end of the molecule. These hydrocarbon ends are not compatible with a polar solvent such as water.\(^4\)
When minute amounts of soaps are put into water, instead of forming simple solutions, the molecules become concentrated at the surface of the water, with the saltlike ends sticking down into the water and the hydrocarbon chains forming a layer on the surface. This arrangement greatly reduces the surface tension of the water and contributes to the startling properties of soap films and bubbles. At higher concentrations, the solutions become turbid as the result of micelle formation. Micelles are sizable aggregates of soap molecules, wherein the hydrocarbon chains form a region of low polarity that is stabilized by having the polar salt ends of the molecules in contact with the water (Figure 18-4).
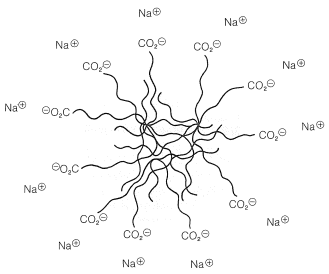
The cleansing action of soap is partly due to the way soap lowers the surface tension of the water thereby helping it to penetrate into fabrics, and also to the ability of the micelles to solubilize oils and greases by taking them into their hydrocarbon regions.
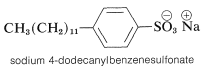
A major disadvantage of the simple carboxylate soaps is that they combine with the calcium and magnesium ions normally present in most tap water to form insoluble scums, which interfere with the cleansing process. Many so-called detergents have been developed that do not have this disadvantage - an example is sodium 4-dodecanylbenzenesulfonate, whose calcium and magnesium salts are water soluble.
When carboxylate salts are put into nonpolar solvents, reversed micelles often are formed, where the polar parts of the molecules are on the inside and the nonpolar parts are on the outside.
Pronounced differences have been observed for the rates of chemical reactions in micelles as compared to pure water. For example, the solvolysis of the 1-methylheptyl sulfonate, \(5\), in dilute water solution proceeds 70 times slower when sufficient sodium dodecanyl sulfate \(\left( \overset{\oplus}{\ce{Na}} \overset{\ominus}{\ce{O}} \ce{SO_3C_{12}H_{25}} \right)\) is added to provide about twice as many dodecanyl sulfate ions in the micelle state as there are molecules of \(5\) present:
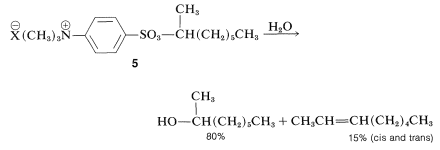
This slowing of the solvolysis reaction by the alkyl sulfate requires that \(5\) be almost completely imprisoned by the micelles, because that part of \(5\) free in water would hydrolyze rapidly. An important result is in the stereochemistry of the reaction, which changes from \(100\%\) inversion with optically active \(5\) in pure water to only \(56\%\) inversion in the micelles. Micelles of the opposite polarity, made from hexadecyltrimethylammonium bromide, \(\ce{C_{16}H_{33}} \overset{\oplus}{\ce{N}} \ce{(CH_3)_3} \overset{\ominus}{\ce{Br}}\), have no effect on the rate of solvolysis of \(5\).
Studies of this type have been made on a number of systems and are of great interest because of the light they may shed on the structure and function of biological membranes.
There is a close resemblance between fatty-acid salts and phospholipids in that both possess long hydrocarbon tails and a polar head. Phospholipids also aggregate in a polar medium to form micelles and continuous bilayer structures such as shown in Figure 18-5. The bilayer lipid structure is very important to the self-sealing function of membranes and their impermeability to very polar molecules.
\(^2\)The electrostatic energy involved in brining two charges from a distance \(r_1\) to a distance \(r_2\) apart is given by \(\left( e_1 e_2/D \right) \left( 1/r_1 - 1/r_2 \right)\), where \(e_1\) and \(e_2\) are the magnitude of the charges and \(D\) is the dielectric constant of the medium (Section 8-7F). If \(e_1\) and \(e_2\) have the same sign, the energy is positive, and with opposite signs the energy is negative. For calibration, the electrostatic energy resulting from bringing a positive charge from a large distance \(\left( 1/r_1 \sim 0 \right)\), up to a negative charge at a distance of \(1\) Å in a vacuum \(\left( D = 1 \right)\) is \(-335 \: \text{kcal mol}^{-1}\).
\(^3\)Until the 19th century soaps were made by boiling animal or vegetable fats with wood ashes, which contain, besides silica, considerable amounts of potassium carbonated. The resulting mixture of potassium carboxylate salts gives a "soft" soap, and this can be converted to a "hard" soap by treatment with excess \(\ce{NaCl}\), which forms the less soluble sodium carboxylate salts. The \(\ce{KCl}\) formed goes into the aqueous phase.
\(^4\)One might well wonder why soap molecules do not simply crystallize out of water solution if the hydrocarbon chains are incompatible with water. However, the crystal packing of the polar salt parts of the molecule is not likely to be very compatible with the hydrocarbon parts and, furthermore, most soaps are salts of mixtures of aliphatic acids and this hardly helps crystallization to occur.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


