4.5: Halogenation of Alkanes. Energies and Rates of Reactions

The economies of the highly industrialized nations of the world are based in large part on energy and chemicals produced from petroleum. Although the most important and versatile intermediates for conversion of petroleum to chemicals are compounds with double or triple bonds, it also is possible to prepare many valuable substances by substitution reactions of alkanes. In such substitutions, a hydrogen is removed from a carbon chain and another atom or group of atoms becomes attached in its place.

A simple example of a substitution reaction is the formation of chloromethane and chlorine:

\[ \ce{CH_4 + Cl_2 \rightarrow CH_3Cl + HCl}\]

The equation for the reaction is simple, the ingredients are cheap, and the product is useful. However, if we want to decide in advance whether such a reaction is actually feasible, we have to know more. Particularly, we have to know whether the reaction proceeds in the direction it is written and, if so, whether conditions can be found under which it proceeds at a convenient rate. Obviously, if one were to mix methane and chlorine and find that, at most, only \(1 \%\) conversion to the desired product occurred and that the \(1 \%\) conversion could be achieved only after a day or so of strong heating, this reaction would be both too unfavorable and too slow for an industrial process.

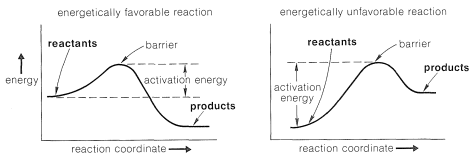
One way of visualizing the problems involved is with energy diagrams, which show the energy in terms of some arbitrary reaction coordinate that is a measure of progress between the initial and final states (Figure 4-4). Diagrams such as Figure 4-4 may not be familiar to you, and a mechanical analogy may be helpful to provide better understanding of the very important ideas involved. Consider a two-level box containing a number of tennis balls. An analog to an energetically favorable reaction would be to have all of the balls

Figure 4-4: Schematic energy diagrams for reactions that are energetically favorable and unfavorable when proceeding from left to right along the reaction coordinate

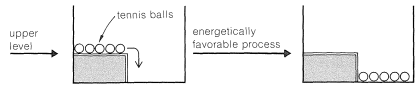
on the upper level where any disturbance would cause them to roll down to the lower level under the influence of gravity, thereby losing energy.

If the upper level is modified and a low fence added to hold the balls in place, it will be just as energetically favorable as when the fence is not there for the balls to be at the lower level. The difference is that the process will not occur spontaneously without some major disturbance. We can say there is an energy barrier to occurrence of the favorable process.

Figure 4-4 where we show an energy barrier to the spontaneous conversion of reactants to products for an energetically favorable chemical reaction.

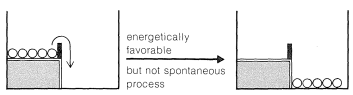
Now, if we shake the box hard enough, the balls on the upper level can acquire enough energy to bounce over the barrier and drop to the lower level. The balls then can be said to acquire enough activation energy to surmount the barrier. At the molecular level, the activation energy must be acquired either by collisions between molecules as the result of their thermal motions, or from some external agency, to permit the reactants to get over the barrier and be transformed into products. We shortly will discuss this more, but first we wish to illustrate another important concept with our mechanical analogy, that of equilibrium and equilibration.

With gentle shaking of our two-level box, all of the balls on the upper level are expected to wind up on the lower level. There will not be enough activation to have them go from the lower to the upper level. In this circumstance, we can say that the balls are not equilibrated between the lower and upper levels. However, if we shake the box vigorously and continuously, no matter whether we start with all of the balls on the lower or upper level, an equilibrium will be set up with, on the average, most of the balls in the energetically more favorable lower level, but some in the upper level as well.

To maintain a constant average fraction of the balls at each level with vigorous and continued shaking, the rate at which balls go from the upper to the lower level must be equal to the rate that they go in the opposite direction. The balls now will be equilibrated between the two levels. At equilibrium, the fraction of the balls on each of the two levels is wholly independent of the height of the barrier, just as long as the activation (shaking) is sufficient to permit the balls to go both ways.

The diagrams of Figure 4-4 are to be interpreted in the same general way. If thermal agitation of the molecules is sufficient, then equilibrium can be expected to be established between the reactants and the products, whether the overall reaction is energetically favorable (left side of Figure 4-4) or energetically unfavorable (right side of Figure 4-4). But as with our analogy, when equilibrium is established we expect the major portion of the molecules to be in the more favorable energy state.

What happens when methane is mixed with chlorine? No measurable reaction occurs when the gases are mixed and kept in the dark at room temperature. Clearly, either the reaction is energetically unfavorable or the energy barrier is high. The answer as to which becomes clear when the mixture is heated to temperatures in excess of \(300^\text{o}\) or when exposed to strong violet or ultraviolet light, whereby a rapid or even explosive reaction takes place. Therefore the reaction is energetically favorable, but the activation energy is greater than can be attained by thermal agitation alone at room temperature. Heat or light therefore must initiate a pathway for the reactants to be converted to products that has a low barrier or activation energy.

Could we have predicted the results of this experiment ahead of time? First, we must recognize that there really are several questions here. Could we have decided whether the reaction was energetically favorable? That the dark reaction would be slow at room temperature? That light would cause the reaction to be fast? We consider these and some related questions in detail because they are important questions and the answers to them are relevant in one way or another to the study of all reactions in organic chemistry.

The Question of the Equilibrium Constant

Presumably, methane could react with chlorine to give chloromethane and hydrogen chloride, or chloromethane could react with hydrogen chloride to give methane and chlorine. If conditions were found for which both reactions proceeded at a finite rate, equilibrium finally would be established when the rates of the reactions in each direction became equal:

\[ \ce{CH_4 + Cl_2 \rightleftharpoons CH_3Cl + HCl}\]

At equilibrium, the relationship among the amounts of reactants and products is given by the equilibrium constant expression

\[K_{eq} = \dfrac{[CH_3Cl][HCl]}{[CH_4][Cl_2]} \label{4-1}\]

in which \(K_\text{eq}\) is the equilibrium constant.

The quantities within the brackets of Equation \(\ref{4-1}\) denote either concentrations for liquid reactants or partial pressures for gaseous substances. If the equilibrium constant \(K_\text{eq}\) is greater than \(1\), then on mixing equal volumes of each of the participant substances (all are gases above \(-24^\text{o}\)), reaction to the right will be initially faster than reaction to the left, until equilibrium is established; at this point there will be more chloromethane and hydrogen chloride present than methane and chlorine. However, if the equilibrium constant were less than \(1\), the reaction initially would proceed faster to the left and, at equilibrium, there would be more methane and chlorine present than chloromethane and hydrogen chloride.\(^4\) For methane chlorination, we know from experiment that the reaction goes to the right and that \(K_\text{eq}\) is much greater than unity. Naturally, it would be helpful in planning other organic preparations to be able to estimate \(K_\text{eq}\) in advance.

It is a common experience to associate chemical reactions with equilibrium constants greater than one with the evolution of heat, in other words, with negative \(\Delta H^\text{0}\) values. There are, in fact, many striking examples. Formation of chloromethane and hydrogen chloride from methane and chlorine has a \(K_\text{eq}\) of \(10^{18}\) and \(\Delta H^\text{0}\) of \(-24 \: \text{kcal}\) per mole of \(CH_3Cl\) formed at \(25^\text{o}\). Combustion of hydrogen with oxygen to give water has a \(K_\text{eq}\) of \(10^{40}\) and \(\Delta H^\text{0} = -57 \: \text{kcal}\) per mole of water formed at \(25^\text{o}\). However, this correlation between \(K_\text{eq}\) and \(\Delta H^\text{0}\) is neither universal nor rigorous. Reactions are known that absorb heat (are endothermic) and yet have \(K_\text{eq} > 1\). Other reactions have large \(\Delta H^\text{0}\) values and equilibrium constants much less than \(1\).

The problem is that the energy change that correlates with \(K_\text{eq}\) is not \(\Delta H^\text{0}\) but \(\Delta G^\text{0}\) (the so-called change of "standard Gibbs energy")\(^5\), and if we know \(\Delta G^\text{0}\), we can calculate \(K_\text{eq}\) by the equation

\[ \Delta G^o =-2.303 RT \log_{10} K_{eq} \label{4-2}\]

in which \(R\) is the gas constant and \(T\) is the absolute temperature in degrees Kelvin. For our calculations, we shall use \(R\) as \(1.987 \: \text{cal} \: \text{deg}^{-1} \: \text{mol}^{-1}\) and you should not forget to convert \(\Delta G^\text{0}\) to \(\text{cal}\).

Tables of \(\Delta G^\text{0}\) values for formation of particular compounds (at various temperatures and states) from the elements are available in handbooks and the literature. With these, we can calculate equilibrium constants quite accurately. For example, handbooks give the following data, which are useful for methane chlorination:

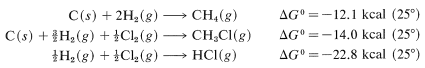
Combining these with proper regard for sign gives

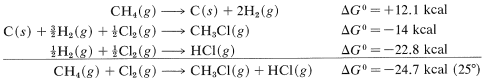
and \(\text{log} \: K_\text{eq} = -\left( -24.7 \times 1000 \right)/ \left(2.303 \times 1.987 \times 298.2 \right)\), so \(K_\text{eq} = 1.3 \times 10^{18}\). Unfortunately, insufficient \(\Delta G^\text{0}\) values for formation reactions are available to make this a widely applicable method for calculating \(K_\text{eq}\) values.

The situation is not wholly hopeless, because there is a relationship between \(\Delta G^\text{0}\) and \(\Delta H^\text{0}\) that also involves \(T\) and another quantity, \(\Delta S^\text{0}\), the standard entropy change of the process:

\[ \Delta G^o = \Delta H^o -T \Delta S^o \label{4-3}\]

This equation shows that \(\Delta G^\text{0}\) and \(\Delta H^\text{0}\) are equal when \(\Delta S^\text{0}\) is zero. Therefore the sign and magnitude of \(T \Delta S^\text{0}\) determine how well \(K_\text{eq}\) correlates with \(\Delta H^\text{0}\). Now, we have to give attention to whether we can estimate \(T \Delta S^\text{0}\) values well enough to decide whether the \(\Delta H^\text{0}\) of a given reaction (calculated from bond energies or other information) will give a good or poor measure of \(\Delta G^\text{0}\).

Entropy and Molecular Disorder

To decide whether we need to worry about \(\Delta S^\text{0}\) with regard to any particular reaction, we have to have some idea what physical meaning entropy has. To be very detailed about this subject is beyond the scope of this book, but you should try to understand the physical basis of entropy, because if you do, then you will be able to predict at least qualitatively whether \(\Delta H^\text{0}\) will be about the same or very different from \(\Delta G^\text{0}\). Essentially, the entropy of a chemical system is a measure of its molecular disorder or randomness. Other things being the same, the more random the system is, the more favorable the system is.

Different kinds of molecules have different degrees of translational, vibrational, and rotational freedom and, hence, different average degrees of molecular disorder or randomness. Now, if for a chemical reaction the degree of molecular disorder is different for the products than for the reactants, there will be a change in entropy and \(\Delta S^\text{0} \neq 0\).

A spectacular example of the effect of molecular disorder in contributing to the difference between \(\Delta H^\text{0}\) and \(\Delta G^\text{0}\) is afforded by the formation of liquid nonane, \(C_9H_{20}\), from solid carbon and hydrogen gas at \(25^\text{o}\):

\[\ce{9C(s) + 10H_2(g) \rightarrow C_910_{20}(l)}\]

with \(\Delta H^o = -54.7 \, kcal\) and \(\Delta S^o = 5.0 \, kcal\).

Equations \(\ref{4-2}\) and \(\ref{4-3}\) can be rearranged to calculate \(\Delta S^\text{0}\) and \(K_\text{eq}\) from \(\Delta H^\text{0}\) and \(\Delta G^\text{0}\):

 

and

\[K_{eq} = 10^{-\Delta G^o/2.303 \,RT} = 10^{-5.900/(2.303 \times 1.987 \times 298.2)} = 4.7 \times 10^{-5}\]

These \(\Delta H^\text{0}\), \(\Delta S^\text{0}\), and \(K_\text{eq}\) values can be compared to those for \(H_2 + \frac{1}{2} O_2 \longrightarrow H_2O\), for which \(\Delta H^\text{0}\) is \(-57 \: \text{kcal}\), \(\Delta S^\text{0}\) is \(8.6 \: \text{e.u.}\), and \(K_\text{eq}\) is \(10^{40}\). Obviously, there is something unfavorable about the entropy change from carbon and hydrogen to nonane. The important thing is that there is a great difference in the constraints on the atoms on each side of the equation. In particular, hydrogen molecules in the gaseous state have great translational freedom and a high degree of disorder, the greater part of which is lost when the hydrogen atoms become attached to a chain of carbons. This makes for a large negative \(\Delta S^\text{0}\), which corresponds to a decrease in \(K_\text{eq}\). The differences in constraints of the carbons are less important. Solid carbon has an ordered, rigid structure with little freedom of motion of the individual carbon atoms. These carbons are less constrained in nonane, and this would tend to make \(\Delta S^\text{0}\) more positive and \(\Delta G^\text{0}\) more negative, corresponding to an increase in \(K_\text{eq}\) (Equations \(\ref{4-2}\) and \(\ref{4-3}\)). However, this is a small effect on \(\Delta S^\text{0}\) compared to the enormous difference in the degree of disorder of hydrogen between hydrogen gas and hydrogen bound to carbon in nonane.

Negative entropy effects usually are observed in ring-closure reactions such as the formation of cyclohexane from 1-hexene, which occur with substantial loss of rotational freedom (disorder) about the \(C-C\) bonds:

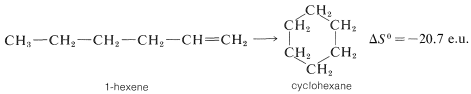
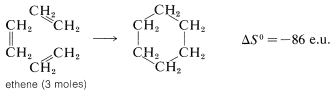
There is an even greater loss in entropy on forming cyclohexane from ethene because substantially more freedom is lost in orienting three ethene molecules to form a ring:

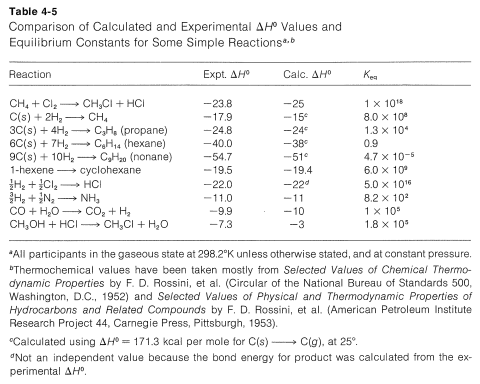
For simple reactions, with the same number of molecules on each side of the equation, with no ring formation or other unusual changes in the constraints between the products and reactants, \(\Delta S^\text{0}\) usually is relatively small. In general, for such processes, we know from experience that \(K_\text{eq}\) usually is greater than 1 if \(\Delta H^\text{0}\) is more negative than \(-15 \: \text{kcal}\) and usually is less than 1 for \(\Delta H^\text{0}\) more positive than \(+15 \: \text{kcal}\). We can use this as a "rule of thumb" to predict whether \(K_\text{eq}\) should be greater or less than unity for vapor-phase reactions involving simple molecules. Some idea of the degree of success to be expected from this rule may be inferred from the examples in Table 4-5, which also contains a further comparison of some experimental \(\Delta H^\text{0}\) values with those calculated from bond energies.

Suppose \(\Delta G^\text{0}\) is positive, what hope do we have of obtaining a useful conversion to a desired product? There is no simple straightforward and general answer to this question. When the reaction is reversible the classic procedure of removing one or more of the products to prevent equilibrium from being established has many applications in organic chemistry, as will be seen later. When this approach is inapplicable, a change in reagents is necessary. Thus, iodine does not give a useful conversion with 2,2-dimethylpropane, \(1\), to give 1-iodo-2,2-dimethylpropane, \(2\), because the position of equilibrium is too far to the left (\(K_\text{eq} \cong 10^{-5}\)):

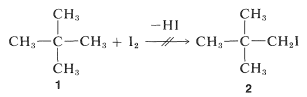
Alternative routes with favorable \(\Delta G^\text{0}\) values are required. Development of ways to make indirectly, by efficient processes, what cannot be made directly is one of the most interesting and challenging activities of organic chemists.

Why Do Methane and Chlorine Fail to React in the Dark at \(25^\text{o}\)?

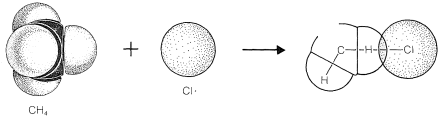
To reach an understanding of why methane and chlorine do not react in the dark, we must consider the details of how the reaction occurs - that is, the reaction mechanism. The simplest mechanism would be for a chlorine molecule to collide with a methane molecule in such a way as to have chloromethane and hydrogen chloride formed directly as a result of a concerted breaking of the \(Cl-Cl\) and \(C-H\) bonds and making of the \(C-Cl\) and \(H-Cl\) bonds (see Figure 4-5). The failure to react indicates that there must be an energy barrier too high for this mechanism to operate. Why should this be so?

Figure 4-5: Four-center collision of chlorine with methane as visualized with ball-and-stick models

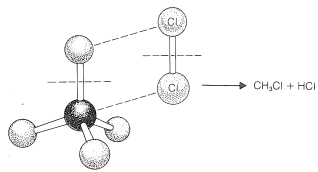
First, this mechanism involves a very precisely oriented "four-center" collision between chlorine and methane that would have a low probability of occurrence (i.e., a large decrease in entropy because a precise orientation means high molecular ordering). Second, it requires pushing a chlorine molecule sufficiently deeply into a methane molecule so one of the chlorine atoms comes close enough to the carbon to form a bond and yield chloromethane.

Figure 4-6: Graph of the potential energy of pairs of neon atoms as a function of the internuclear distance. The energy values are per mole of neon atoms.

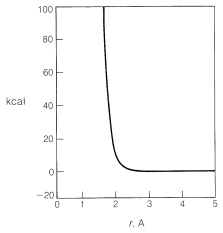
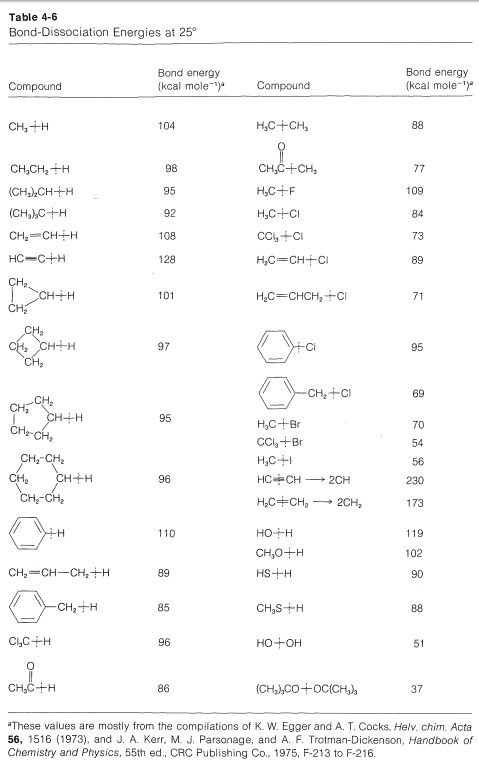
Generally, to bring nonbonded atoms to near-bonding distances (\(1.2 \: \text{A}\) to \(1.8 \: \text{A}\)) requires a large expenditure of energy, as can be seen in Figure 4-6. Interatomic repulsive forces increase rapidly at short distances, and pushing a chlorine molecule into a methane molecule to attain distances similar to the \(1.77\)-\(\text{A}\) carbon-chlorine bond distance in chloromethane would require a considerable amount of compression (see Figure 4-7). Valuable information

Figure 4-7: Models showing the degree of atomic compression required to bring a chlorine molecule to within bonding distance of carbon and hydrogen of methane

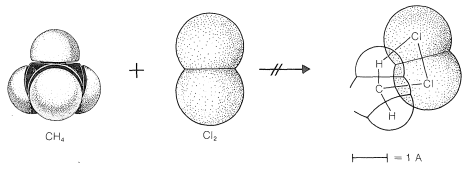
about interatomic repulsions can be obtained with space-filling models of the CPK type (Section 2-2), which have radii scaled to correspond to actual atomic interference radii, that is, the interatomic distance at the point where curves of the type of Figure 4-6 start to rise steeply. With such models, the degree of atomic compression required to bring the nonbonded atoms to within near-bonding distance is more evident than with the ball-and-stick models. It may be noted that four-center reactions of the type postulated in Figure 4-5 are encountered only rarely.

If the concerted four-center mechanism for formation of chloromethane and hydrogen chloride from chlorine and methane is discarded, all the remaining possibilities are stepwise reaction mechanisms. A slow stepwise reaction is dynamically analogous to the flow of sand through a succession of funnels with different stem diameters. The funnel with the smallest stem will be the most important bottleneck and, if its stem diameter is much smaller than the others, it alone will determine the flow rate. Generally, a multistep chemical reaction will have a slow rate-determining step (analogous to the funnel with the small stem) and other relatively fast steps, which may occur either before or after the slow step.

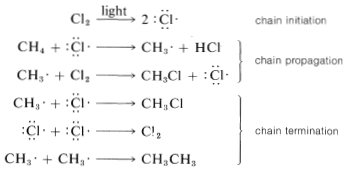
A possible set of steps for the chlorination of methane follows:

Reactions (1) and (2) involve dissociation of chlorine into chlorine atoms and the breaking of a \(C-H\) bond of methane to give a methyl radical and a hydrogen atom. The methyl radical, like chlorine and hydrogen atoms, has one election not involved in bonding. Atoms and radicals usually are highly reactive, so formation of chloromethane and hydrogen chloride should proceed readily by Reactions (3) and (4). The crux then will be whether Steps (1) and (2) are reasonable under the reaction conditions.

In the absence of some external stimulus, only collisions due to the usual thermal motions of the molecules can provide the energy needed to break the bonds. At temperatures below \(100^\text{o}\), it is very rare indeed that the thermal agitation alone can supply sufficient energy to break any significant number of bonds stronger than \(30\) to \(35 \: \text{kcal mol}^{-1}\).

The \(Cl-Cl\) bond energy from Table 4-3 is \(58.1 \: \text{kcal}\), which is much too great to allow bond breaking from thermal agitation at \(25^\text{o}\) in accord with Reaction (1). For Reaction (2) it is not advisable to use the \(98.7 \: \text{kcal} \: C-H\) bond energy from Table 4-3 because this is one fourth of the energy required to break all four \(C-H\) bonds (Section 4-3). More specific bond-dissociation energies are given in Table 4-5, and it will be seen that to break one \(C-H\) bond of methane requires \(104 \: \text{kcal}\) at \(25^\text{o}\), which again is too much to be gained by thermal agitation. Therefore we can conclude that Reactions (1)-(4) can not be an important mechanism for chlorination of methane at room temperature.

One might ask whether dissociation into ions would provide viable mechanisms for methane chlorination. Part of the answer certainly is: Not in the vapor phase, as the following thermochemical data show:

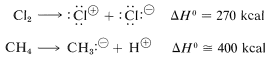
Ionic dissociation simply does not occur at ordinarily accessible temperatures by collisions between molecules in the vapor state. What is needed for formation of ions is either a highly energetic external stimulus, such as bombardment with fast-moving electrons, or an ionizing solvent that will assist ionization. Both of these processes will be discussed later. The point here is that ionic dissociation is not a viable step for the vapor-phase chlorination of methane.

Why Does Light Induce the Chlorination of Methane?

First, we should make clear that the light does more than provide energy merely to lift the molecules of methane and chlorine over the barrier of Figure 4-4. This is evident from the fact that very little light is needed, far less than one light photon per molecule of chloromethane produced. The light could activate either methane or chlorine, or both. However, methane is colorless and chlorine is yellow-green. This indicates that chlorine, not methane, interacts with visible light. A photon of near-ultraviolet light, such as is absorbed by chlorine gas, provides more than enough energy to split the molecule into two chlorine atoms:

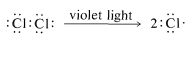
Once produced, a chlorine atom can remove a hydrogen atom from a methane molecule and form a methyl radical and a hydrogen chloride molecule. The bond-dissociation energies of \(CH_4\) (\(104 \: \text{kcal}\)) and \(HCl\) (\(103.1 \: \text{kcal}\)) suggest that this reaction is endothermic by about \(1 \: \text{kcal}\):

Figure 4-8). The methyl radical resulting from the attack of atomic chlorine on a hydrogen of methane then can remove a chlorine atom from molecular chlorine and form chloromethane and a new chlorine atom:

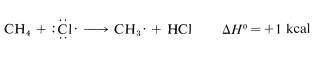
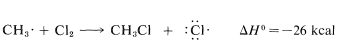
Use of bond-dissociation energies gives a calculated \(\Delta H^\text{0}\) of \(-26 \: \text{kcal}\) for this reaction, which is certainly large enough, by our rule of thumb, to predict that \(K_\text{eq}\) will be greater than 1. Attack of a methyl radical on molecular chlorine is expected to require somewhat more oriented collision than for a chlorine atom reacting with methane (the chlorine molecule probably should be endwise, not sidewise, to the radical) but the interatomic repulsion probably should not be much different.

The net result of \(CH_4 + Cl \cdot \longrightarrow CH_3 \cdot + HCl\) and \(CH_3 \cdot + Cl_2 \longrightarrow CH_3Cl + Cl \cdot\) is formation of chloromethane and hydrogen chloride from methane and chlorine. Notice that the chlorine atom consumed in the first step is replaced by another one in the second step. This kind of sequence of reactions is called a chain reaction because, in principle, one atom can induce the reaction of an infinite number of molecules through operation of a "chain" or cycle of reactions. In our example, chlorine atoms formed by the action of light on

Figure 4-7.

\(Cl_2\) can induce the chlorination of methane by the chain-propagating steps:

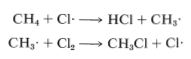
In practice, chain reactions are limited by so-called termination processes. In our example, chlorine atoms or methyl radicals are destroyed by reacting with one another, as shown in the following equations:

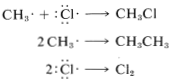
Chain reactions may be considered to involve three phases: First, chain initiation must occur, which for methane chlorination is activation and conversion of chlorine molecules to chlorine atoms by light. Second, chain-propagation steps convert reactants to products with no net consumption of atoms or radicals. The propagation reactions occur in competition with chain-terminating steps, which result in destruction of atoms or radicals. Putting everything together, we can write:

The chain-termination reactions are expected to be exceedingly fast because atoms and radicals have electrons in unfilled shells that normally are bonding. As a result, bond formation can begin as soon as the atoms or radicals approach one another closely, without need for other bonds to begin to break. The evidence is strong that bond-forming reactions between atoms and radicals usually are diffusion-controlled, that there is almost no barrier or activation energy required, and the rates of combination are simply the rates at which encounters between radicals or atoms occur.

If the rates of combination of radicals or atoms are so fast, you might well wonder how chain propagation ever could compete. Of course, competition will be possible if the propagation reactions themselves are fast, but another important consideration is the fact that the atom or radical concentrations are very low. Suppose that the concentration of \(Cl \cdot\) is \(10^{-11} \: \text{M}\) and the \(CH_4\) concentration \(1 \: \text{M}\). The probability of encounters between two \(Cl \cdot\) atoms will be proportional to \(10^{-11} \times 10^{-11}\), and between \(CH_4\) and \(Cl \cdot\) atoms it will be \(10^{-11} \times 1\). Thus, other things being the same, \(CH_4 + Cl \cdot \longrightarrow CH_3 \cdot + HCl\) (propagation) would be favored over \(2Cl \cdot \longrightarrow Cl_2\) (termination) by a factor of \(10^{11}\). Under favorable conditions, the methane-chlorination chain may go through 100 to 10,000 cycles before termination occurs by radical or atom combination. Consequently the efficiency (or quantum yield) of the reaction is very high in terms of the amount of chlorination that occurs relative to the amount of the light absorbed.

The overall rates of chain reactions usually are slowed very much by substances that can combine with atoms or radicals and convert them into species incapable of participating in the chain-propagation steps. Such substances are called radical traps, or inhibitors. Oxygen acts as an inhibitor in the chlorination of methane by rapidly combining with a methyl radical to form the comparatively stable (less reactive) peroxymethyl radical, \(CH_3OO \cdot\). This effectively terminates the chain:

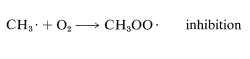
Can We Predict Whether Reactions Will Be Fast or Slow?

To a considerable degree, we can predict relative reactivities, provided we use common sense to limit our efforts to reasonable situations. In the preceding section, we argued that reactions in which atoms or radicals combine can well be expected to be extremely fast because each entity has a potentially bonding electron in an outer unfilled shell, and bringing these together to form a bond does not require that other bonds be broken:

Figure 4-6). As \(CH_4\) and \(Cl \cdot\) get closer together, the new bond starts to form and the old bond starts to break. At the top of the barrier, the hydrogen will be bonded partly to chlorine and partly to carbon, \(\left[ Cl - - - H - - - CH_3 \right]\), and this we call the activated complex or transition state. The concept of the transition state is an important one, which we will use repeatedly later in connection with many other kinds of reactions. The value of the concept lies in the fact that the reacting system, when it reaches the top of the barrier, can be though of as a chemical entity with a particular, even if not well-defined, structure and definite thermodynamic properties.

The difference between the average energy of the reactants and the energy of the transition state is called the activation energy (Figure 4-4). We expect this energy to be smaller (lower barrier) if a weak bond is being broken and a strong bond is being made. The perceptive reader will notice that we are suggesting a parallel between reaction rate and \(\Delta H^\text{0}\) because \(\Delta H^\text{0}\) depends on the difference in strengths of the bonds being broken and formed. Yet previously (Section 4-4A), we pointed out that the energy barrier for a reaction need bear no relationship to how energetically feasible the reaction is, and this is indeed true for complex reactions involving many steps. But our intuitive parallel between rate and \(\Delta H^\text{0}\) usually works quite well for the rates of individual steps. This is borne out by experimental data on rates of removal of a hydrogen atom from methane by atoms or radicals (\(X \cdot\)), such as \(F \cdot\), \(Cl \cdot\), \(Br \cdot\), \(HO \cdot\), \(H_2N \cdot\), which generally parallel the strength of the new bond formed:

Similarly, if we look at the \(H-C\) bond-dissociation energies of the hydrocarbons shown in Table 4-6, we would infer that \(Cl \cdot\) would remove a hydrogen most rapidly from the carbon forming the weakest \(C-H\) bond and, again, this is very much in accord with experience. For example, the chlorination of methylbenzene (toluene) in sunlight leads to the substitution of a methyl hydrogen rather than a ring hydrogen for the reason that the methyl \(C-H\) bonds are weaker and are attacked more rapidly than the ring \(C-H\) bonds. This can be seen explicitly in the \(\Delta H^\text{0}\) values for the chain-propagation steps calculated from the bond-dissociation energies of Table 4-6.

Methyl substitution (observed):

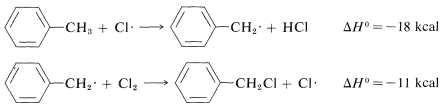
Ring substitution (not observed):

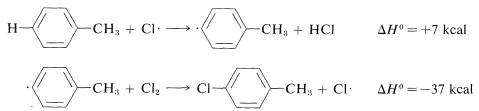
The \(\Delta H^\text{0}\) of ring-hydrogen abstraction is unfavorable by \(+7 \: \text{kcal}\) because of the high \(C-H\) bond energy (\(110 \: \text{kcal}\)). Thus this step is not observed. It is too slow in comparison with the more favorable reaction at the methyl group even though the second propagation step is energetically favorable by \(-37 \: \text{kcal}\) and presumably would occur very rapidly. Use of bond-dissociation energies to predict relative reaction rates becomes much less valid when we try to compare different kinds of reactions. To illustrate, ethane might react with \(F \cdot\) to give fluoromethane or hydrogen fluoride:

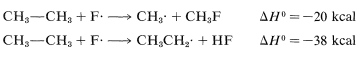
It is not a good idea to try to predict the relative rates of these two reactions on the basis of their overall \(\Delta H^\text{0}\) values because the nature of the bonds made and broken is too different.

How Should We Go about Formulating a Reaction Mechanism?

Faced with proposing a mechanism for a reaction that involves overall making or breaking of more than two bonds, the beginner almost invariably tries to concoct a process wherein, with a single step, all of the right bonds break and all of the right bonds form. Such mechanisms, called concerted mechanisms, have three disadvantages. First, they are almost impossible to prove correct. Second, prediction of the relative rates of reactions involving concerted mechanisms is especially difficult. Third, concerted mechanisms have a certain sterility in that one has no control over what happens while they are taking place, except an overall control of rate by regulating concentrations, temperature, pressure, choice of solvents, and so on.

To illustrate, suppose that methane chlorination appeared to proceed by way of a one-step concerted mechanism:

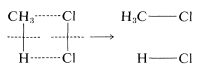
At the instant of reaction, the reactant molecules in effect would disappear into a dark closet and later emerge as product molecules. There is no way to prove experimentally that all of the bonds were made and formed simultaneously. All one could do would be to use the most searching possible tests to probe for the existence of discrete steps. If these tests fail, the reaction still would not be proved concerted because other, still more searching tests might be developed later that would give a different answer. The fact is, once you accept that a particular reaction is concerted, you, in effect, accept the proposition that further work on its mechanism is futile, no matter how important you might feel that other studies would be regarding the factors affecting the reaction rate.

The experienced practitioner in reaction mechanisms accepts a concerted mechanism for a reaction involving the breaking and making of more than two bonds as a last resort. He first will try to analyze the overall transformation in terms of discrete steps that are individually simple enough surely to be concerted and that also involves energetically reasonable intermediates.

Such an analysis of a reaction in terms of discrete mechanistic steps offers many possibilities for experimental studies, especially in development of procedures for detecting the existence, even if highly transitory, of the proposed intermediates. We shall give many examples of the fruitfulness of this kind of approach in subsequent discussions.

\(^4\)If calculations based on chemical equilibrium constants are unfamiliar to you, we suggest you study one of the general chemistry texts listed for supplemental reading at the end of Chapter 1.

\(^5\)Many books and references use \(\Delta F^\text{0}\) instead of \(\Delta G^\text{0}\). The difference between standard Gibbs energy \(\Delta G^\text{0}\) and the Gibbs energy \(\Delta G\) is that \(\Delta G^\text{0}\) is defined as the value of the free energy when all of the participants are in standard states. The free energy for \(\Delta G\) for a reaction \(\text{A} + \text{B} + \cdots \longrightarrow \text{X} + \text{Y} + \cdots\) is equal to \(\Delta G^\text{0} - 2.303 RT \: \text{log} \: \frac{\left[ \text{X} \right] \left[ \text{Y} \right] \cdots}{\left[ \text{A} \right] \left[ \text{B} \right] \cdots}\) where the products, \(\left[ \text{X} \right], \left[ \text{Y} \right] \cdots\), and the reactants, \(\left[ \text{A} \right], \left[ \text{B} \right] \cdots\), do not have to be in standard states. We shall use only \(\Delta G^\text{0}\) in this book.

\(^6\)The entropy unit \(\text{e.u.}\) has the dimensions calorie per degree or \(\text{cal deg}^{-1}\).

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."