4.4: Combustion. Heats of Reaction. Bond Energies

Last updated
Save as PDF

Page ID: 22172

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

All hydrocarbons are attacked by oxygen at elevated temperatures and, if oxygen is in excess, complete combustion occurs to carbon dioxide and water:

\[ CH_4 + 2O_2 \rightarrow CO_Edit2 + 2H_2O\]

The heat evolved in this process - the heat of the combustion reaction, \(\Delta H\) - is a measure of the amount of energy stored in the \(C-C\) and \(C-H\) bonds of the hydrocarbon compared to the energy stored in the products, carbon dioxide and water. It can be measured experimentally with considerable accuracy and generally is reported as \(\Delta H^\text{0}\) the amount of heat (in kilocalories)\(^2\) liberated on complete combustion of one mole of hydrocarbon when the reactants and the products are in standard states, and at the same temperature, usually \(25^\text{o}\).\(^3\) Not all chemical reactions that occur spontaneously liberate heat - some actually absorb heat. By convention, \(\Delta H^\text{0}\) is given a negative sign when heat is evolved (exothermic reaction) and a positive sign when heat is absorbed (endothermic reaction). The heat evolved or absorbed also is called the enthalpy change.

For the combustion of \(1 \: \text{mol}\) of methane at \(15^\text{o}\), we find by experiment (corrected from constant volume to constant pressure, if necessary) that the reaction is exothermic by \(212.8 \: \text{kcal}\). This statement can be expressed as follows:

\[ CH_4(g) + 2O_2(g) \rightarrow CO_2 (g) + 2H_2O (l)\]

with \(\Delta H^o = -212.8 \, kcal\).

The symbol \(\left( g \right)\) denotes that the reactants and products are in the gaseous state except for the water, which is liquid \(\left( l \right)\). If we wish to have \(\Delta H^\text{0}\) with gaseous water \(H_2O \: \left( g \right)\) as the product we have to make a correction for the heat of vaporization of water (\(10.5 \: \text{kcal} \: \text{mol}^{-1}\) at \(25^\text{o}\)):

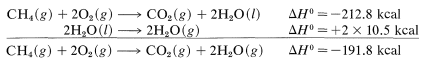
Top reaction: C H 4 gas plus 2 O 2 gas goes to C O 2 gas plus 2 H 2 O liquid with delta H of -212.8 kcal. Middle reaction: 2 H 2 O liquid goes to 2 H 2 O gas with delta H of 2 times 10.5 kcal. These combine to get the reaction: C H 4 gas plus 2 O 2 gas goes to C O 2 gas plus 2 H 2 O gas with delta H of -191.8 kcal.

The task of measuring the heats of all chemical reactions is a formidable one and about as practical as counting grains of sand on the beach. However, it is of practical interest to be able to estimate heats of reaction, and this can be done quite simply with the aid of bond energies. The necessary bond energies are given in Table 4-3, and it is important to notice that they apply only to complete dissociation of gaseous substances to gaseous atoms at \(25^\text{o}C\). Also, they do not apply, without suitable corrections, to many compounds, such as benzene, that have more than one double bond. This limitation will be discussed in Chapters 6 and 21.

To calculate \(\Delta H^\text{0}\) for the combustion of one mole of methane, first we break bonds as follows, using \(98.7 \: \text{kcal} \: \text{mol}^{-1}\) for the energy of each of the

Table of bond energies.

\(C-H\) bonds,

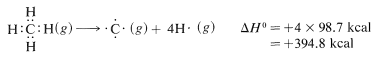
C H 4 gas goes to C gas plus 4 H gas with delta H of 4 times 98.7 kcal or +394.8 kcal.

and then \(118.9 \: \text{kcal} \: \text{mol}^{-1}\) for the energy of the double bond in oxygen:

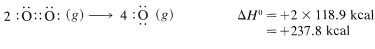
2 O 2 gas goes to 4 O gas with delta H of 2 times 118.9 kcal or +237.8 kcal.

Then we make bonds, using \(192 \: \text{kcal} \: \text{mol}^{-1}\) for each \(O=C\) bond in carbon dioxide,

C gas plus 2 O gas goes to C O 2 gas with delta H of -2 times 192.0 kcal or -384.0 kcal.

and \(110.6 \: \text{kcal} \: \text{mol}^{-1}\) for each of the \(H-O\) bonds in water:

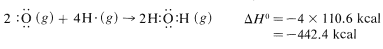
2 O gas plus 4 H gas goes to 2 H 2 O gas with delta H of -4 times 110.6 kcal or -442.4 kcal.

The net sum of these \(\Delta H^\text{0}\) values is \(394.8 + 237.8 - 384.0 - 442.4 = -193.8 \: \text{kcal}\), which is reasonably close to the value of \(-191.8 \: \text{kcal}\) for the heat of combustion of one mole of methane determined experimentally.

The same type of procedure can be used to estimate \(\Delta H^\text{0}\) values for many other kinds of reactions of organic compounds in the vapor phase at \(25^\text{o}\). Moreover, if appropriate heats of vaporization are available, it is straightforward to compute \(\Delta H^\text{0}\) for vapor-phase reactions of substances which are normally liquids or solids at \(25^\text{o}\). The special problems that arise when solutions and ionic substances are involved are considered in Chapters 8 and 11.

It is important to recognize that the bond energies listed in Table 4-3 for all molecules other than diatomic molecules are average values. That the \(C-H\) bond energy is stated to be \(98.7 \: \text{kcal}\) does not mean that, if the hydrogens of methane were detached one by one, \(98.7 \: \text{kcal}\) would have to be put in at each step. Actually, the experimental evidence is in accord with quite different energies for the separate dissociation steps:

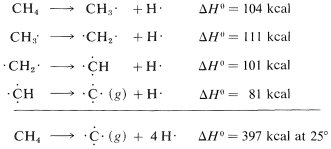
Reactions from top to bottom: 1. C H 4 goes to C H 3 plus H with delta H of 104 kcal. 2. C H 3 goes to C H 2 plus H with delta H of 111 kcal. 3. C H 2 goes to C H plus H with delta H of 101 kcal. 4. C H goes to C gas plus H with delta H of 81 kcal. These combine to get the reaction C H 4 goes to C gas plus C gas plus 4 H with delta H of 397 kcal at 25 degrees.

The moral is that we should try to avoid using the bond energies in Table 4-3 as a measure of \(\Delta H^\text{0}\) for the dissociation of just one bond in a polyatomic molecule. For this we need what are called bond-dissociation energies, some of which are given in Table 4-6. The values given have been selected to emphasize how structure influences bond energy. Thus, \(C-H\) bond energies in alkanes decrease in the order primary \(>\) secondary \(>\) tertiary; likewise, \(C-H\) bonds decrease in strength along the series \(C \equiv C-H \: > \: C=C-H \: > \: C-C-H\).

How accurate are \(\Delta H^\text{0}\) values calculated from bond energies? Generally quite good provided nonbonded interactions between the atoms are small and the bond angles and distances are close to the normal values (Section 2-2B). A few examples of calculated and experimental heats of combustion of some hydrocarbons are given in Table 4-4. Negative discrepancies represent heats of combustion smaller than expected from the average bond energies and positive values correspond to larger than expected heats of combustion.

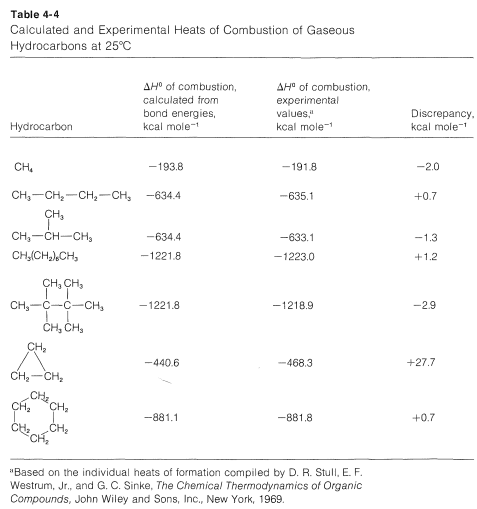
Table of calculated and experimental heats of combustion at gaseous hydrocarbons at 25 degrees C.

Comparing isomers in Table 4-4, we see that 2-methylpropane and 2,2,3,3-tetramethylbutane give off less heat when burned than do butane and octane, and this is a rather general characteristic result of chain branching.

Cyclopropane has a \(\Delta H^\text{0}\) of combustion of \(27.7 \: \text{kcal} \: \text{mol}^{-1}\) greater than expected from bond energies, and this clearly is associated with the abnormal \(C-C-C\) bond angles in the ring. These matters will be discussed in detail in Chapter 12. For cyclohexane, which has normal bond angles, the heat of combustion is close to the calculated value.

\(^2\)In this book we use kilocalories in place of the presently recommended (SI) joules for units of energy. As of the date of writing, it is not clear just how general the use of the joule will become among chemists. To convert calories to joules (or \(\text{kcal}\) to \(\text{kJ}\)), multiply by 4.184.

\(^3\)You may wonder how a reaction, such as combustion of methane, can occur at \(25^\text{o}\). The fact is that the reaction can be carried out at any desired temperature. The important thing is that the \(\Delta H^\text{0}\) value we are talking about here is the heat liberated or absorbed when you start with the reactants at \(25^\text{o}\) and finish with the products at \(25^\text{o}\). As long as \(\Delta H^\text{0}\) is defined this way, it does not matter at what temperature the reaction actually occurs. Standard states for gases are \(1 \: \text{atm}\) partial pressure. Standard states for liquids or solids usually are the pure liquid or solid at \(1 \: \text{atm}\) external pressure.

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."