27.9: Ion-Cyclotron Resonance
- Page ID
- 22391
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A gaseous ion in a magnetic field moves in a circular orbit with an angular frequency \(\omega_c\) such that \(\omega_c = \left( e/m \right) \left( H_0/c \right)\), in which \(e/m\) is the ratio of charge to mass, \(H_0\) is the applied magnetic field, and \(c\) is the velocity of light. The frequency \(\omega_c\) is called the "cyclotron frequency" and is the basis of the cyclotron particle accelerator used in nuclear physics. Now suppose a radio-frequency field is imposed on the ions from a variable oscillator, as shown in Figure 27-15. When the frequency of the oscillator \(\omega\) equals \(\omega_c\), the ions absorb energy and move faster through larger orbits, but at the same frequency \(\omega_c\).
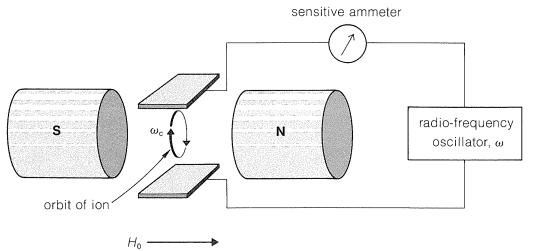
Ion-cyclotron resonance combines features of mass spectroscopy in that the ratio \(e/m\) is involved, and of NMR spectroscopy in that detection depends on absorption of energy from a radio-frequency oscillator. The chemical applications depend on reactions between the ions during the time they remain in the cyclotron, which may be many seconds. Suppose then that we generate \(\ce{OH}^\ominus\) by electron bombardment of a gaseous mixture of water and 2-methyl-2-propanol (tert-butyl alcohol). The \(\ce{OH}^\ominus\) ion can be detected by its characteristic frequency \(\omega = \left( e/m \right) \left( H_0/c \right)\), in which \(e/m = 1/17\). Now, because the reaction \(\ce{(CH_3)_3COH} + \ce{OH}^\ominus \rightarrow \ce{(CH_3)_3CO}^\ominus + \ce{H_2O}\) occurs, a new ion of \(e/m = 1/73\) appears. The reverse reaction, \(\ce{(CH_3)_3CO}^\ominus + \ce{H_2O} \rightarrow \ce{(CH_3)_3COH} + \ce{OH}^\ominus\), does not occur to a measurable extent. From this we can infer that \(\ce{(CH_3)_3COH}\) is a stronger acid than \(\ce{H_2O}\) in the gas phase. These experiments clearly are related to chemical-ionization mass spectroscopy (Section 27-7), and provide the basis for determining the gas-phase acidities of alkynes and water, discussed in Section 11-8. A detailed gas-phase acidity scale has been established by this means.
Many unusual reactions occur between ions and neutral molecules in the gas phase, which can be detected by ion-cyclotron resonance; a few examples are
\[\ce{CH_3F^+} \: \text{(from electron impact)} + \ce{CH_3F} \rightarrow \ce{CH_3} \overset{+}{\ce{F}} \ce{H} + \cdot \ce{CH_2F} \: \text{(} \ce{H} \cdot \: \text{atom transfer)}\]
\[\ce{CH_3FH^+} + \ce{N_2} \rightarrow \ce{CH_3N_2^+} + \ce{HF} \: \: \: \: \: \text{(nucleophilic displacement)}\]
\[\ce{CH_3FH^+} + \ce{Xe} \rightarrow \ce{CH_3Xe^+} + \ce{HF} \: \: \: \: \: \text{(nucleophilic displacement)}\]
Clearly, in gas-phase reactions \(\ce{HF}\) is an extremely good leaving group in being rapidly displaced both by \(\ce{Xe}\) and \(\ce{N_2}\). From our discussions of leaving groups in Section 8-7C, we can infer that \(\ce{H_2F}^\oplus\) must be a very strong acid in the gas phase and the available evidence indicates that this is so.
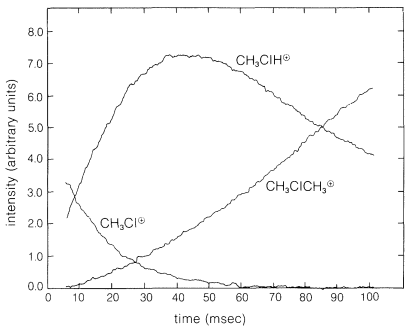
It is possible to measure the concentrations of the ions as a function of time and thus determine the rates of reaction of ions with neutral molecules in the gas phase. Figure 27-16 shows the results of a typical experiment wherein a sequence of reactions occurs that involves chloromethane as the neutral molecule and begins with the ion \(\ce{CH_3Cl}^\oplus\) formed by a short burst \(\left( 10 \: \text{msec} \right)\) of \(16 \: \text{KeV}\) electrons. The originally formed \(\ce{CH_3Cl}^\oplus\) ions react with \(\ce{CH_3Cl}\) to yield \(\ce{CH_3ClH}^\oplus + \cdot \ce{CH_2Cl}\). The buildup of \(\ce{CH_3ClH}^\oplus\) and the disappearance of \(\ce{CH_3Cl}^\oplus\) clearly are coupled. A slower reaction, \(\ce{CH_3ClH}^\oplus + \ce{CH_3Cl} \rightarrow \ce{(CH_3)_2Cl}^\oplus + \ce{HCl}\), then takes over the action.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


