19.4: Enantiomeric Purity
- Page ID
- 22300
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The term enantiomeric purity (or optical purity) is defined as the fractional excess of one enantiomer over the other. This is expressed in Equation 19-4 in terms of the moles (or weights) of the two enantiomers, \(n_1\), and \(n_2\), and is equal to the ratio of the observed optical rotation, \(\alpha_\text{obs}\), and to the optical rotation of either pure enantiomer, \(\alpha_0\):
\[\text{enantiomeric purity of } n_1 = \dfrac{n_1-n_2}{n_1+n_2} = \dfrac{\alpha_\text{obs}}{\alpha_0} \tag{19-4}\]
Thus a racemic mixture (\(n_1 = n_2\)) has an enantiomeric purity of zero. Any other enantiomeric composition in principle can be determined provided the mixture has a measurable rotation and the rotation of the pure enantiomer, \(\alpha_0\), is known. Unfortunately, there is no simple method of calculating \(\alpha_0\), in advance. In fact, specific rotations of optically pure compounds are determined most reliably from Equation 19-4 after measurement of enantiomeric purity by independent methods.
Virtually all of the methods for determining enantiomeric purity rely on the differences in chemical, physical, or spectroscopic properties of diastereomers derived from enantiomeric mixtures. We will mention here two of the most straightforward methods, based on gas-liquid chromatography and nuclear magnetic resonance.
Determination of Enantiomeric Purity by Gas Chromatography
This method amounts to a complete resolution of the type described in Section 19-3D, but on an analytical scale. For example, assume that you have a partially resolved compound, \(A\), consisting of unequal amounts of the enantiomers \(A_+\) and \(A_-\). By reaction with a second chiral enantiomerically pure substance, \(B_+\), A is converted to a mixture of diastereomers \(A_+B_+\) and \(A_-B_+\). Because these diastereomers are chemically and physically different, the mixture usually can be analyzed by gas-liquid chromatography (Section 9-2A). If the reaction of \(B_+\) with \(A_+\) and \(A_-\) was quantitative, the relative areas of the two peaks eluting from the column correspond to the ratio of the diastereomers \(A_+B_+/A_-B_+\), and thus to the ratio of enantiomers \(A_+/A_-\), from which the enantiomeric purity of the partially resolved mixture can be calculated.
An alternative and very direct approach is to separate the enantiomers on a column in which the stationary liquid phase is a chiral compound. The diastereomeric interaction is between \(A_+\) or \(A_-\) and the chiral liquid phase, and may be sufficiently different to permit separation of \(A_+\) from \(A_-\). The ratio of the amounts of \(A_+\) and \(A_-\) corresponds to the enantiomeric purity.
Determination of Enantiomeric Purity by NMR Spectroscopy
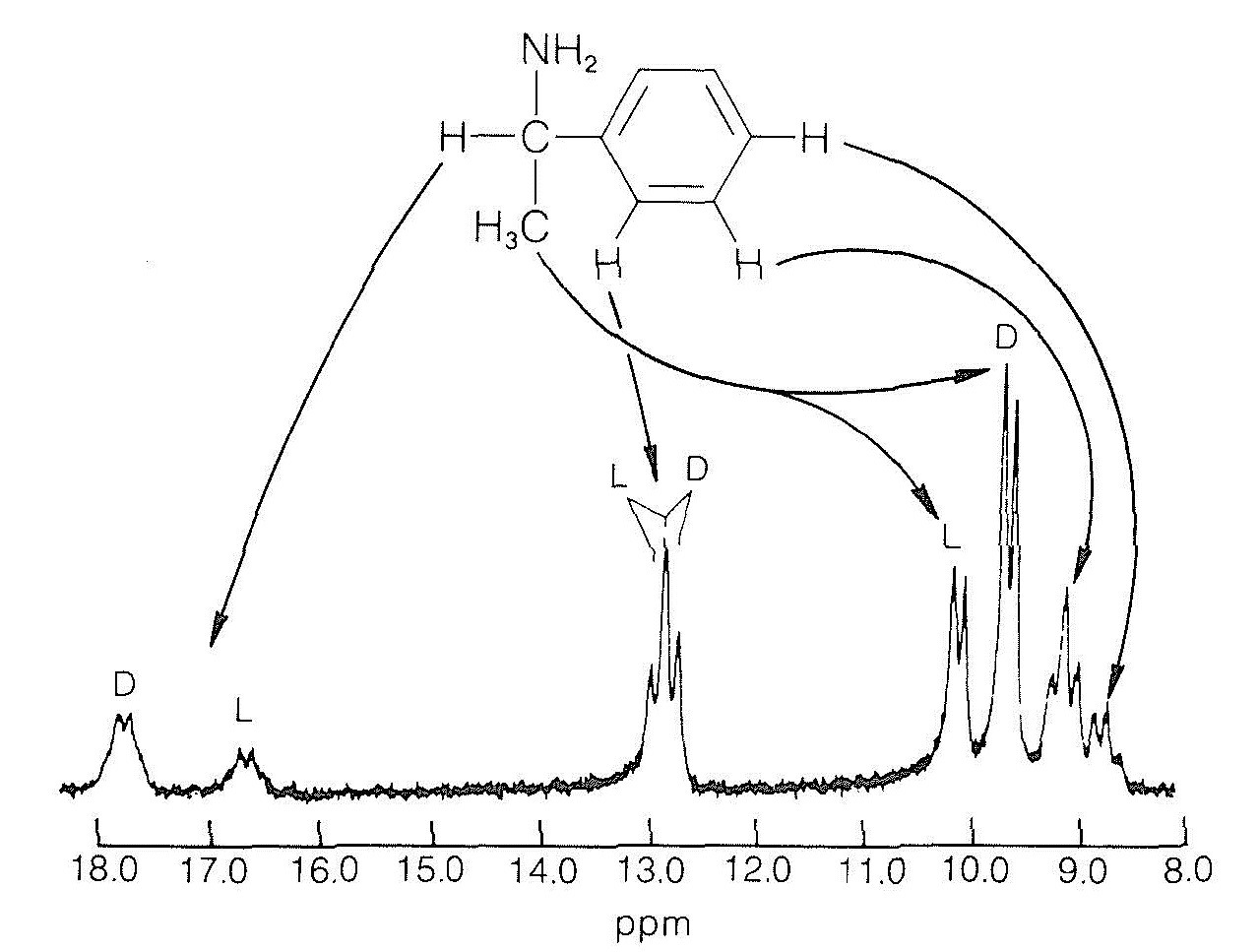
The nmr chemical shifts of nuclei of enantiomeric compounds \(A_+\) and \(A_-\) are identical in achiral solvents. However, in a chiral solvent (enantiomerically pure) \(A_+\) and \(A_-\) will be effectively converted to diastereomers as the result of chiral solvation and, accordingly, their nuclei will have nonidentical chemical shifts. Provided that the shift differences are large enough to permit the resonances of one chirally solvated enantiomer to be resolved from those of the other, the ratio of enantiomers \(A_+/A_-\) can be determined from the ratio of their corresponding nmr signal intensities.
Alternatively, with a pure chiral reagent the enantiomeric mixture may be converted (quantitatively) to diastereomers. The nuclei of the diastereomeric compounds are expected to have small differences in chemical shifts, even in achiral solvents, and integration of their respective signal intensities should correspond to the ratio of diastereomers, and hence to the ratio of enantiomers in the original mixture.
Application of the above-described nmr methods for the determination of enantiomeric composition is difficult, if not impossible, if the chemical-shift differences are too small \(\left( 0.02 \: \text{ppm} \right)\) or if the resonances overlap extensively. This problem often can be solved by utilizing the ability of certain chelates of rare earth metals (the lanthanide metals) to complex with organic compounds, particularly with alcohols, ketones, amines, and other Lewis bases. Chemical shifts in the presence of even small amounts of lanthanide chelates usually are spread over a much wider range of field strengths than for the pure compounds. As discussed previously in Sections 9-10D and 9-10K, increasing chemical shifts can greatly simplify otherwise complex nmr spectra. The shifts are produced by these lanthanide compounds because the electrons on the metal atoms are not all paired, so that the metal atoms are paramagnetic (possess a net electron spin). In an applied magnetic field the unpaired electrons circulate around the metal atoms and produce an induced field (Figure 9-26) which, depending on the nature of the metal, can act either to increase or reduce the applied magnetic field, \(H_0\).
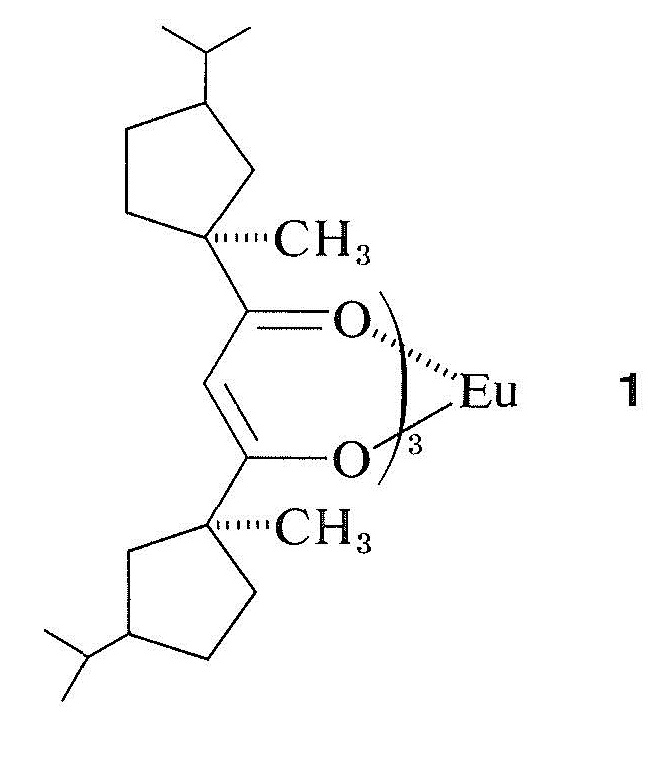
In the complex formed between the lanthanide reagent and the organic substrate, the chemical shifts most strongly affected are those of nuclei close to the paramagnetic metal atom. The resonances of these nuclei also are broadened by the paramagnetic metal (Section 27-1), and this is undesirable. The lanthanide complexes that produce these large shift changes are called shift reagents. Most of them are chelate salts of substituted 2,4-pentanediones, especially of 2,2,6,6-tetramethyl-3,5-heptanedione (Section 17-8).
There are several useful shift reagents, usually of europium, in which the organic ligands are chiral. An example is \(1\):