27.2: Line-Width Differences in NMR
- Page ID
- 22377
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)If you look at the NMR spectra of many different kinds of organic compounds, you will notice that some resonances are sharp and others are broad. In a few spectra, all of the peaks may be broad as the result of poor spectrometer performance, but this is not true for the spectra of Figures 9-29 and 24-2 where, within a given spectrum, some resonances will be seen to be sharp and others broad. We can understand these differences by consideration of the lifetimes of the magnetic states between which the NMR transitions occur.\(^1\) The lifetimes of the states can be related to the width of the lines by the Heisenberg uncertainty principle.
You may have heard of the uncertainty principle, but if you have not studied chemical physics you may have little idea of its possible importance to organic chemistry. The usual statement of the principle is that there are limits to how precisely we can specify the momentum and the position of a particle at the same time. An alternative statement has more relevance to spectroscopy and chemistry, namely, that the precision with which we can define the energy of a state depends on the lifetime of the state. The shorter the lifetime, the less the certainty with which we can define the energy.\(^2\)
Let us consider an example. Suppose a magnetic nucleus in a ground state with a long lifetime and rather precisely defined energy goes to an excited state with a short lifetime, \(\Delta t\).\(^3\) The uncertainty principle tells us that the energy of the excited state cannot be defined precisely. It will have an inherent uncertainty in its energy so that an imprecise \(\nu\), having uncertainty in frequency \(\Delta \nu\), will take the nucleus from the ground state to the excited state. The imprecision of the energy \(\Delta \Delta E\), or the imprecision \(\Delta \nu\) in the transition frequency, \(\nu\), depends on \(\Delta t\), and is given approximately by the relationship
\[\Delta \Delta E \sim \frac{h}{2 \pi} \times \frac{1}{\Delta t} \sim h \Delta \nu \tag{27-1}\]
in which \(h\) is Planck's constant. What this means is that the absorption line corresponding to the transition will have an uncertainty in line width that is inversely proportional to \(\Delta t\) (see Figure 27-1).
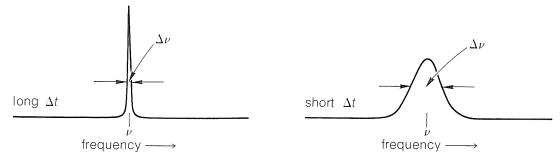
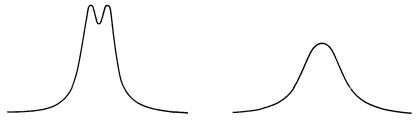
It is most convenient to think of line widths in frequency units because most of our spectra are plotted this way. If the scale is wavelength or energy, it can be converted to frequency by the procedures given previously (Section 9-3). Division of Equation 27-1 by \(h\) leads to the relationship \(\Delta \nu \sim 1/ \left(2 \pi \times \Delta t \right)\). In NMR spectroscopy, we may wish to consider spin-spin splittings or chemical shifts involving lines no farther than \(1 \: \text{Hz}\) apart. However, two lines \(1 \: \text{Hz}\) apart will not be clearly distinguishable unless \(\Delta \nu\) of each is less than about \(1 \: \text{Hz}\), which corresponds to a \(\Delta t\), the lifetime of the excited state, of \(1/ \left( 2 \pi \right) \cong 0.16 \: \text{sec}\). If \(\Delta \nu\) is \(\geq 2 \: \text{Hz}\), lines that are \(1 \: \text{Hz}\) apart will be so poorly resolved as to appear as one line (cf. Figure 27-2). A \(\Delta \nu\) of \(2 \: \text{Hz}\) corresponds to a \(\Delta t\) of \(1/ \left( 2 \times 2 \pi \right) \cong 0.08 \: \text{sec}\). Clearly, line separations observed in NMR spectroscopy and, in fact, in all forms of spectroscopy, depend on the lifetimes of the states between which transitions take place. The lifetime of \(0.16 \: \text{sec}\) required for \(\Delta \nu\) to be \(1 \: \text{Hz}\) is a long time for a molecule! During \(0.16 \: \text{sec}\), a molecule such as ethanol in the liquid phase may undergo \(10^{11}\) collisions with other molecules, \(10^{10}\) rotations about the \(\ce{C-C}\) bonds, and \(10^{12}\) vibrations of each of the various bonds, and may even undergo a number of chemical changes. The properties of magnetic states that have lifetimes of this order clearly must be an average over all of these happenings.
It is possible to shorten the lifetime of an excited nuclear magnetic state (or increase its relaxation rate) in a number of ways. For a liquid, the simplest way is to dissolve in it paramagnetic metal ions, such as \(\ce{Cu}\)(II), \(\ce{Fe}\)(III), \(\ce{Mn}\)(II), and the like, or other substances (\(\ce{O_2}\), \(\ce{NO}\), and so on) that have unpaired electrons. Another way is to reduce the rate of motion of magnetic nuclei in different molecules with respect to one another, which is easily done by increasing the viscosity. Without going into details of the mechanisms by which substances with unpaired electrons or increased viscosity shorten the lifetime of excited nuclear magnetic states, it is important to know that dramatic line broadening thereby can be produced. Thus the proton resonance line of water is enormously broadened by adding paramagnetic \(\ce{Mn}\)(II) ions or by freezing (water molecules in ice move much more slowly relative to one another than in liquid water).
Notes
- It may be helpful to you before proceeding to review the introductions to Section 9-10 and 9-10A in which the general characteristics of the nuclear magnetic states are described.
- A brief exposition of the basis of the uncertainty principle is given by R. P. Feynman, Lectures in Physics, Addison-Wesley, Reading, Mass., 1963, Vol. 1, pp. 6-10.
- The uncertainty principle will be applied in this section to NMR spectroscopy but, as we will see later, it is applicable to all other forms of spectroscopy.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


