19.5: Absolute And Relative Configuration
- Page ID
- 22761
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The sign of rotation of plane-polarized light by an enantiomer is not easily related to its configuration. This is true even for substances with very similar structures. Thus, given lactic acid, \(\ce{CH_3CHOHCO_2H}\), with a specific rotation \(+3.82^\text{o}\), and methyl lactate, \(\ce{CH_3CHOHCO_2CH_3}\), with a specific rotation \(-8.25^\text{o}\), we cannot tell from the rotation alone whether the acid and ester have the same or a different arrangement of groups about the chiral center. Their relative configurations have to be obtained by other means.
If we convert \(\left( + \right)\)-lactic acid into its methyl ester, we can be reasonably certain that the ester will be related in configuration to the acid, because esterification should not affect the configuration about the chiral carbon atom. It happens that the methyl ester so obtained is levorotatory, so we know that \(\left( + \right)\)-lactic acid and \(\left( - \right)\)-methyl lactate have the same relative configuration at the asymmetric carbon, even if they possess opposite signs of optical rotation. However, we still do not know the absolute configuration; that is, we are unable to tell which of the two possible configurations of lactic acid, \(2a\) or \(2b\), corresponds to the dextro or \(\left( + \right)\)-acid and which to the levo or \(\left( - \right)\)-acid:
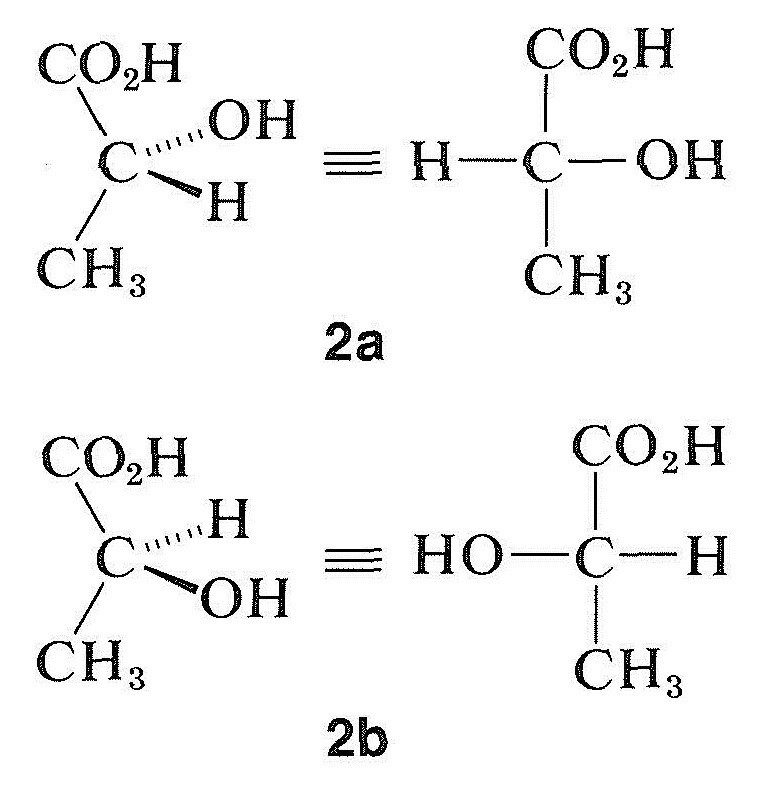
Until 1956, the absolute configuration of no optically active compound was known. Instead, configurations were assigned relative to a standard, glyceraldehyde, which originally was chosen by E. Fischer (around 1885) for the purpose of correlating the configuration of carbohydrates. Fischer arbitrarily assigned the configuration \(3a\) to dextrorotatory glyceraldehyde, which was known as \(D\)-\(\left( + \right)\)-glyceraldehyde. The levorotatory enantiomer, \(3b\), is designated as \(L\)-\(\left( - \right)\)-glyceraldehyde. (If you are unsure of the terminology \(D\) and \(L\), or of the rules for writing Fischer projection formulas, review Sections 5-3C and 5-4.)
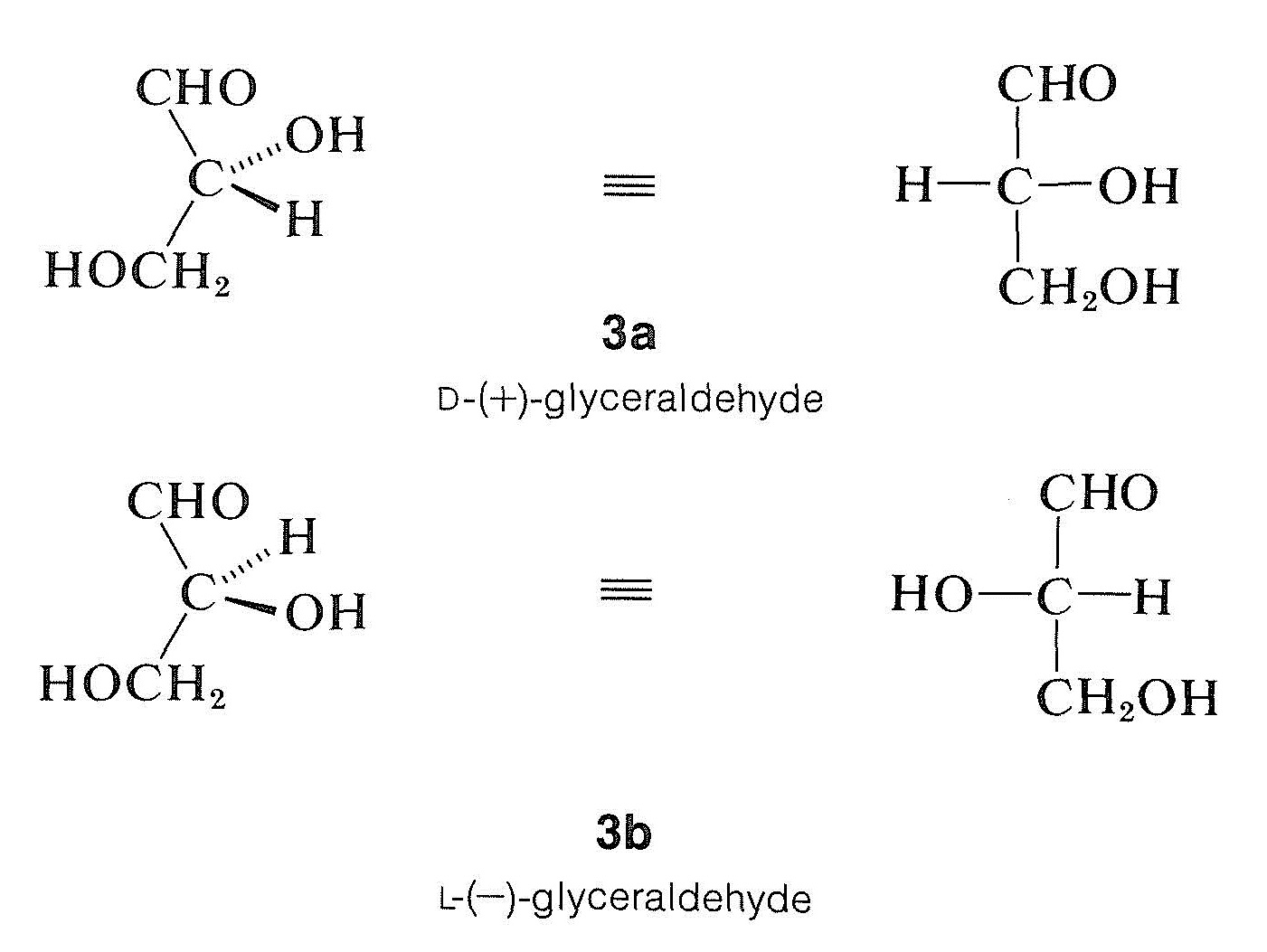
The configurations of many compounds besides sugars now have been related to glyceraldehyde, including \(\alpha\)-amino acids, terpenes, steroids, and other biochemically important substances. Compounds whose configurations are related to \(D\)-\(\left( + \right)\)-glyceraldehyde are said to belong to the \(D\) series, and those related to \(L\)-\(\left( - \right)\)-glyceraldehyde belong to the \(L\) series.
At the time the choice of absolute configuration for glyceraldehyde was made, there was no way of knowing whether the configuration of \(\left( + \right)\)-glyceraldehyde was in reality \(3a\) or \(3b\). However, the choice had a \(50\%\) chance of being correct, and we now know that \(3a\), the \(D\) configuration, is in fact the correct configuration of \(\left( + \right)\)-glyceraldehyde. This was established through use of a special x-ray crystallographic technique, which permitted determination of the absolute disposition of the atoms in space of sodium rubidium \(\left( + \right)\)-tartrate. The configuration of \(\left( + \right)\)-tartaric acid (Section 5-5) previously had been shown by chemical means to be opposite to that of \(\left( + \right)\)-glyceraldehyde. Consequently the absolute configuration of any compound now is known once it has been correlated directly or indirectly with glyceraldehyde. For example,

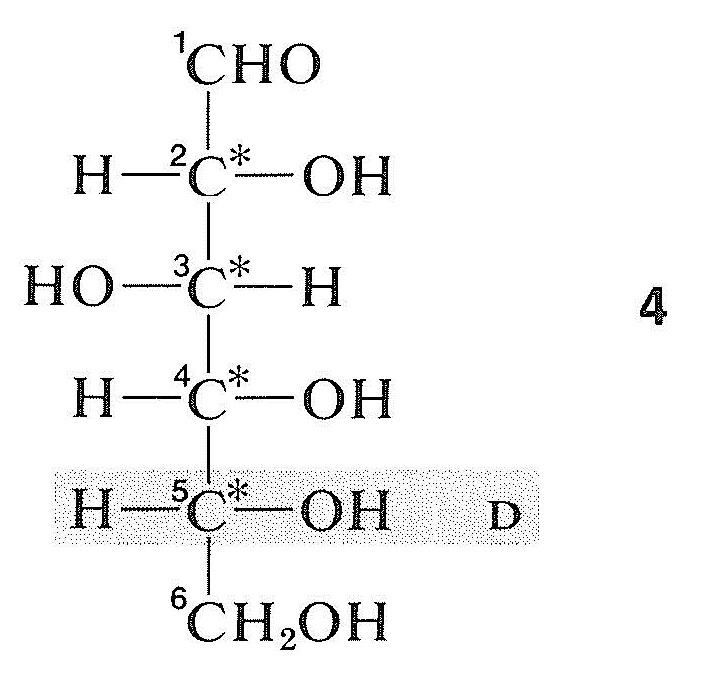
When there are several chiral carbons in a molecule, the configuration at one center usually is related directly or indirectly to glyceraldehyde, and the configurations at the other centers are determined relative to the first. Thus in the aldehyde form of the important sugar, \(\left( + \right)\)-glucose, there are four chiral centers, and so there are \(2^4 = 16\) possible stereoisorners. The projection formula of the isomer that corresponds to the aldehyde form of natural glucose is \(4\). By convention for sugars, the configuration of the highest-numbered chiral carbon is referred to glyceraldehyde to determine the overall configuration of the molecule. For glucose, this atom is \(\ce{C5}\), next to the \(\ce{CH_2OH}\) group, and has the hydroxyl group on the right. Therefore, naturally occurring glucose, which has a \(\left( + \right)\) rotation, belongs to the \(D\) series and is properly called \(D\)-\(\left( + \right)\)-glucose:
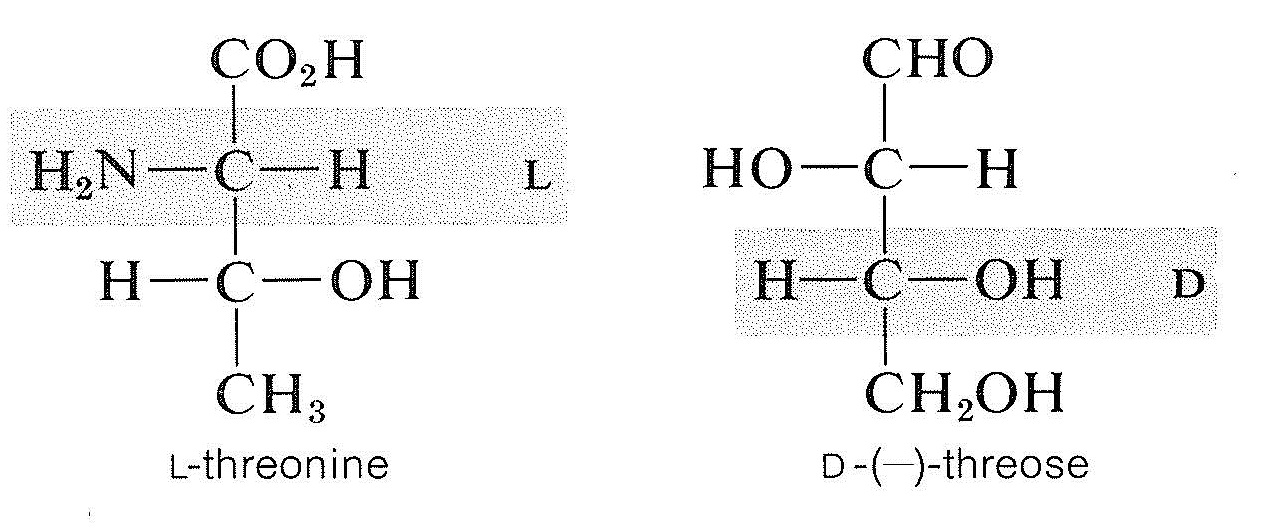
However, the configurations of \(\alpha\)-amino acids possessing more than one chiral carbon are determined by the lowest-numbered chiral carbon, which is the carbon alpha to the carboxyl group. Thus, even though the natural \(\alpha\)-amino acid, threonine, has exactly the same kind of arrangement of substituents as the natural sugar, threose, threonine by the amino-acid convention belongs to the \(L\)-series, whereas threose by the sugar convention belongs to the \(D\)-series:
A serious ambiguity arises for compounds such as the active tartaric acids. If the amino-acid convention is used, \(\left( + \right)\)-tartaric acid falls in the \(D\) series; by the sugar convention, it has the \(L\) configuration. One way out of this dilemma is to use the subscripts \(s\) and \(g\) to denote the amino-acid or carbohydrate conventions, respectively. Then the absolute configuration of \(\left( + \right)\)-tartaric acid can be designated as either \(D_s\)-\(\left( + \right)\)-tartaric acid of \(L_g\)-\(\left( + \right)\)-tartaric acid.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


