5.6: Molecules with More Than One Chiral Center. Diastereomers

We have seen examples of molecules with one chiral center that exist in two mirror-image configurations, which we call enantiomers. What happens when there is more than one chiral center? How many stereoisomers should we expect? Consider the stereoisomers of the important amino acid, threonine, (2-amino-3-hydroxybutanoic acid). For this substance, if we write all of the possible configurations of its two chiral carbons, we have four different projection formulas, \(19\)-\(22\), corresponding to four different stereoisomers:

Figure 5-12) and by putting the model over \(20\)-\(22\) verify that none of these projections have the configurations of both chiral carbons the same as your model of \(19\).

Figure 5-12, except that configurations at each of two atoms are involved. Next, the model is turned and rotated around the center \(C-C\) bond to put the methyl and carboxyl groups anti to one another. The Newman formula is then drawn to correspond to the ball-and-stick model.

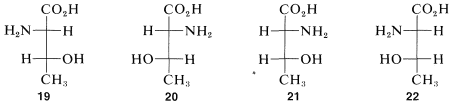
Because each chiral center added to a chain doubles the number of possible configurations, we expect eight different stereoisomers with three chiral carbons, sixteen with four, and so on, the simple rule the is \(2^n\) possible different stereoisomers for \(n\) chiral centers. As we shall see later, this rule has to be modified in some special cases.

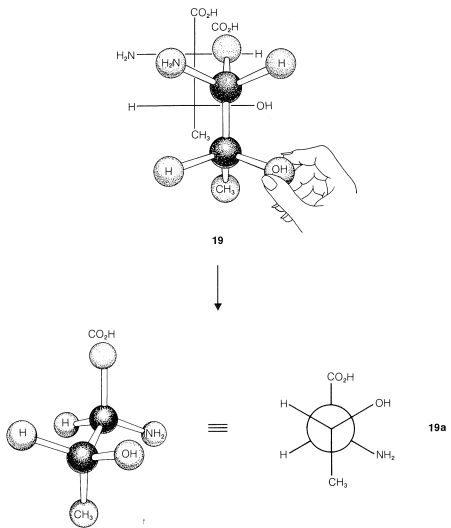
What is the relationship between stereoisomers \(19\)-\(22\)? This will be clearer if we translate each of the projection formulas into a three-dimensional representation, as shown in Figure 5-13. You will be helped greatly if you work through the sequence yourself with a ball-and-stick model. Drawn as Newman projections, \(19\)-\(22\) come out as shown in \(19a\)-\(22a\):

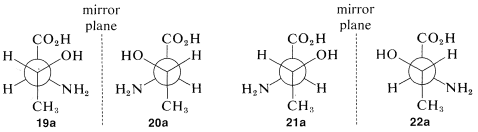
It should be clear (and, if it isn't, ball-and-stick models will be invaluable) that \(19a\) and (20a\) are mirror images of one another and that \(21a\) and \(22a\) are similarly mirror images.\(^5\) What about other combinations such as \(19a\) and \(21a\) or \(20a\) and \(22a\)? If you look at the pairs closely you will find that they are not mirror images and are not identical. Such substances, related to each other in this way and which can be converted one into the other only by changing the configurations at one or more chiral centers, are called diastereomers.

The difference between enantiomers and diastereomers is more than just geometry. Diastereomers have substantially different chemical and physical properties, whereas enantiomers have identical physical properties (apart from their optical rotations). This is illustrated in Table 5-1 for the threonine stereoisomers. The reason for the difference in physical properties between diastereomers can be seen very simply for a substance with two chiral centers by noting that a right shoe on a right foot (\(D,D\)) is a mirror image, or has the same physical properties, as a left shoe on a left foot (\(L,L\)), but is not a mirror image, nor does it have the same physical properties, as a left show on a right foot (\(L,D\)), or a right shoe on a left foot (\(D,L\)).

Meso Compounds (Achiral Diastereomers)

All of the threonine stereoisomers \(19\)-\(22\) are chiral substances; that is, they are not identical with their mirror images. However, it is important to recognize that not all diastereomers are chiral. To illustrate this point, we return to the tartaric acids mentioned previously in connection is Pasteur's discoveries (Section 5-1C).

Proceeding as we did for threonine, we can write four projection formulas for tartaric acid, 2,3-dihydroxybutanedioic acid, as shown by \(23\)-\(26\):

Figure 5-13.)

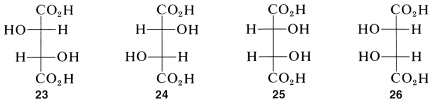
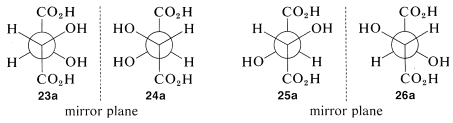
There are two pairs of mirror images \(23a\) and \(24a\), as well as \(25a\) and \(26a\). However, what will not be so immediately clear, but what you must verify for yourself is that \(25a\) and \(26a\) are, in fact, identical. This means that \(25a\) and \(26a\) are representations of a single achiral substance, identical with its mirror image. Substances that have chiral centers but are themselves achiral are called meso compounds.

The condition that makes possible the existence of meso compounds is an appropriate degree of molecular symmetry. There are several kinds of such molecular symmetry. In the case of projection formulas \(25\) (or \(26\)) there is a plane of symmetry, which means that a plane can be placed through the molecule such that one half of the molecule is a mirror image of the other half. The mirror plane for meso-tartaric acid can be seen easily from its projection formulas \(25b\) and \(26b\). These two formulas are superimposable if one is rotated \(180^\text{o}\) in the plane of the paper.

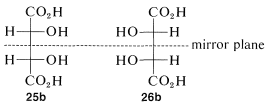
The Newman representations \(25a\) and \(26a\) of meso-tartaric acid does not have a mirror plane. Why is it different from the Fischer projections in this respect? The reason is that the projection formulas represent a particular eclipsed conformation \(27\) of meso-tartaric acid that does have a mirror plane:

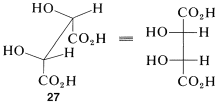
Therefore, if you are confronted with a particular sawhorse or Newman formula and you have to decide whether it represents a meso compound, the best procedure is to make a ball-and-stick model of the conformation and then rotate around the bonds to see if it can be brought into a conformation (staggered or eclipsed) that has a plane of symmetry (such as \(27\)) or is identical with its mirror image.

As expected from our previous discussions diastereomers of tartaric acid have different physical properties (Table 5-2).

If you find yourself confused about the \(D,L\) and meso forms of tartaric acid, a simple analogy may help keep matters straight. Consider three sets of shoes. A right shoe beside a left shoe is a meso combination with a plane of symmetry. A left shoe next to a left shoe is not identical with, but is

the mirror image of, a right shoe next to a right shoe. None of the three combinations are identical. Each right or left shoe corresponds to a right or left configuration of a tartaric acid carbon so the three sets correspond to meso-, \(L\)-, and \(D\)-tartaric acid, respectively.

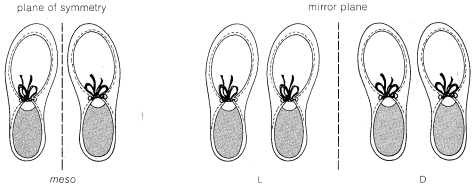
There is another symmetry test for meso configurations that is applicable to staggered conformations and can be illustrated with the tartaric acids. If you make models of \(25a\) and \(26a\) you will find that they are mirror images and identical but, as we have said, they have no plane of symmetry. In this conformation, the molecules do have a center of symmetry. Thus a line drawn at any angle through the midpoint of the central \(C-C\) bond of \(25a\) (or \(26a\)) has an identical environment on each side of the midpoint. Another way of putting it is that each half of the molecule is the photographic image (i.e., reverse) of the other half. For a molecule with chiral centers, if its projection formula has a plane of symmetry or if we can find a rotational conformation with either a plane or center of symmetry, then it will be meso and achiral.

The idea that for every \(n\) chiral centers there can be \(2^n\) different configurations will be true only if none of the configurations has sufficient symmetry to be identical with its mirror image. For every meso form there will be one less pair of enantiomers and one less total number of possible configurations than is theoretically possible according to the number of chiral centers. At most, one meso compounds is possible for structures with four chiral centers. An example is offered by the meso forms of tetrahydroxyhexanedioic acid which, with four chiral atoms, have configurations \(28\) and \(29\):

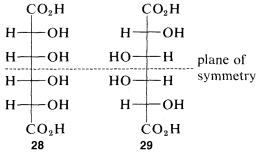
\(^5\)The same information can be obtained from projection formulas. You can see that projections \(19\) and \(20\) are mirror images and that \(20\), \(21\), or \(22\) can not be superimposed on \(19\). However, in some situations confusion can result in making such comparisons and it is important to be able to translate the projection formulas into ball-and-stick models or perspective drawings.

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."