5.4: Representation of Organic Structure

Many problems in organic chemistry require consideration of structures in three dimensions, and it is very helpful to use molecular models to visualize the relative positions of the atoms in space. Unfortunately, we are forced to communicate three-dimensional concepts by means of drawings in two dimensions, and not all of us are equally gifted in making or visualizing such drawings. Obviously, communication by means of drawings, such as those in Figure 5-5 and 5-7, would be impractically difficult and time consuming, thus some form of abbreviation is necessary.

Conformational Drawings

Two styles of abbreviating the eclipsed and staggered conformations of ethane are shown in Figure 5-9; in each, the junction of lines representing bonds is assumed to be a carbon atom. Using the "sawhorse" convention, we always consider that we are viewing the molecule slightly from above and from the right, and it is understood that the central \(C-C\) bond is perpendicular to the plane of the paper. With the "Newman" convention, we view the molecule directly down the \(C-C\) bond axis so the carbon in front hides the carbon behind. The circle is only a visual aid to help distinguish the bonds of the back carbon from those of the front carbon. The rear atoms in the eclipsed conformation are drawn slightly offset from a truly eclipsed view so the bonds to them can be seen.

Figure 5-9: Conventions for showing the staggered and eclipsed conformations of ethane

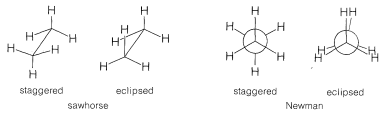
The staggered conformations of butane are shown in Figure 5-10 in both the sawhorse and Newman conventions. There is little to choose between the two conventions for simple ethane derivatives, but the sawhorse convention is strongly favored for representing the conformations of ring compounds such as cyclohexane. The resemblance between the gauche forms of butane and the most stable conformation of cyclohexane is strikingly apparent in the sawhorse representations of both, as shown in Figure 5-10. Notice that the ring carbons of cyclohexane do not lie in one plane and that all the bond angles are tetrahedral. The conformations of this interesting and important molecule are discussed in detail in Chapter 12.

Figure 5-10: Sawhorse and Newman conventions for showing the staggered conformations of butane. Only one gauche form is shown. Cyclohexane is shown to emphasize the resemblance of its stable conformation to the gauche conformation of butane.

Despite the usefulness of the sawhorse-type drawing, cyclic molecules often are drawn with planar rings and distorted bond angles even though the rings actually may not be planar. The reason for this is partly that planar rings are easier to draw and partly to emphasize the configuration of attached groups, irrespective of the conformation. Typical examples follow:

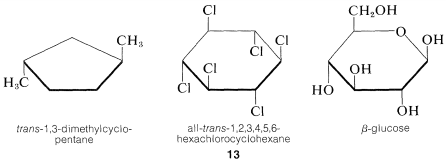
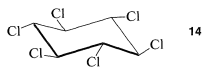
Generally we shall avoid such drawings and suggest that it is much better to learn to draw molecules in as nearly correct perspective as possible. Once the sawhorse representation of cyclohexane is mastered, it is almost as easy to drawn \(14\) as \(13\), and \(14\) is much more informative about the shape of the molecule:

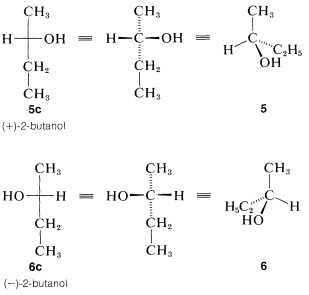
We have indicated how the enantiomers of 2-butanol differ by drawing their strutures \(5\) and \(6\) (Section 5-1D) in perspective to show the tetrahedral configuration of substituents at the chiral carbon. This configuration also can be represented by the sawhorse or Newman formulas using any one of the several possible staggered conformations such as \(5a\) and \(6a\) or \(5b\) and \(6b\):

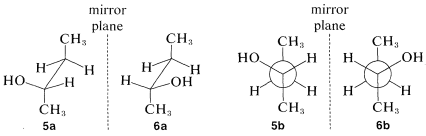
These drawings are clear but can be cumbersome, particularly for more complex molecules, and we shortly shall describe other means of representing the configurations of chiral molecules.

Planar Structures

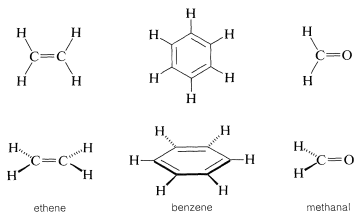
Planar molecules such as benzene, ethene, and methanal are best drawn in the plane of the paper with bond angles of about \(120^\text{o}\). When it is desired to draw them as viewed on edge (out of plane) care must be taken to provide proper perspective. The forward bonds can be drawn with slightly heavier lines; a tapered bond indicates direction, the wide end pointing toward the viewer and the narrow end away from the viewer (Figure 5-11). Barred lines are used here to indicate a rear or receding bond (many writers use dashed lines, but these may be confused with other uses of dashed lines, as for partial bonds).

However, you will find other representations of planar carbons with rather grossly distorted bond angles. For example, methanoic acid is planar with nearly \(120^\text{o}\) bond angles, but often is drawn with \(H-C-O\) angles of \(90^\text{o}\) and \(180^\text{o}\):

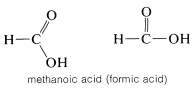
The distorted structures commonly are used to save space and, regretfully, we have to use them very frequently for this reason.

Projection Formulas

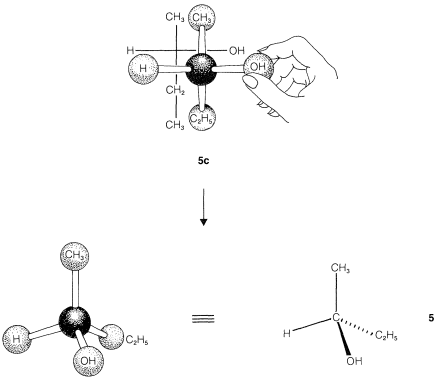
The sawhorse or Newman representations of 2-butanol, \(5a\) and \(5b\) and \(6a\) and \(6b\), are excellent for showing the arrangements of the atoms in conformations, but are needlessly complex for representing the stereochemical configuration. Fischer projection formulas are widely used to show configurations and are quite straightforward, once one gets the idea of what they represent..

Figure 5-11: Front and side views of planar molecules showing some conventions used to indicate perspective

The projection formulas of 2-butanol are \(5c\) and \(6c\):

Figure 5-12.

Figure 5-12: Procedure for relating a projection formula to a configurational drawing with the aid of a ball-and-stick model. Assemble the ball-and-stick model over the projection formula (here \(5c\)) so that the groups are arranged by the convention of the formula (horizontal bonds out, vertical bonds back), then turn the model so the appropriate groups, here \(CH_3\) and \(H\), are parallel to the plane of the paper and make the perspective drawing agree with the model. The reverse procedure translates the perspective drawing into the projection formula.

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."