5.3: Conformational Isomers
- Page ID
- 22177
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When using ball-and-stick models, if one allows the sticks to rotate in the holes, it will be found that for ethane, \(CH_3-CH_3\), an infinite number of different atomic orientations are possible, depending on the angular relationship (the so-called torsional angle) between the hydrogens on each carbon. Two extreme orientations or conformations are shown in Figure 5-5. In end-on views of the models, the eclipsed conformation is seen to have the hydrogens on the forward carbon directly in front of those on the back carbon. The staggered conformation has each of the hydrogens on the forward carbon set between each of the hydrogens on the back carbon. It has not been possible to obtain separate samples of ethane that correspond to these or intermediate orientations because actual ethane molecules appear to have essentially "free rotation" about the single bond joining the carbons. Free, or at least rapid, rotation is possible around all \(C-C\) single bonds, except when the carbons are part of a ring as in cyclopropane or cyclohexane.
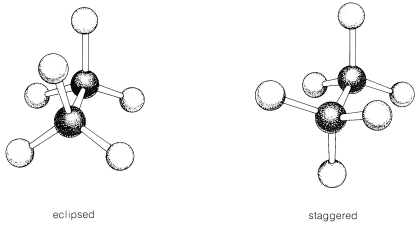
For ethane and its derivatives, the staggered conformations are more stable than the eclipsed conformations. The reason for this in ethane is not wholly clear, but doubtless depends on the fact that, in the staggered conformation, the \(C-H\) bonding electrons are as far away from one another as possible and give the least interelectronic repulsion. With groups larger than hydrogen atoms substituted on ethane carbons, space-filling models usually show less interference (steric hindrance) for staggered conformations than for eclipsed conformations.
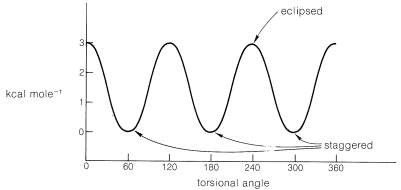
The energy difference between eclipsed and staggered ethane is approximately \(3 \: \text{kcal mol}^{-1}\).\(^4\) This is shown in Figure 5-6 as the height of the peaks (eclipsed forms) separating the valleys (staggered forms) on a curve showing the potential energy of ethane as the methyl groups rotate with respect to each other through \(360^\text{o}\). Rotation then is not strictly "free" because there is a \(3\)-\(\text{kcal mol}^{-1}\) energy barrier to overcome on eclipsing the hydrogens. Even so, the barrier is low enough that rotation is very rapid at room temperature, occurring on the order of \(10^{10}\) times per second.
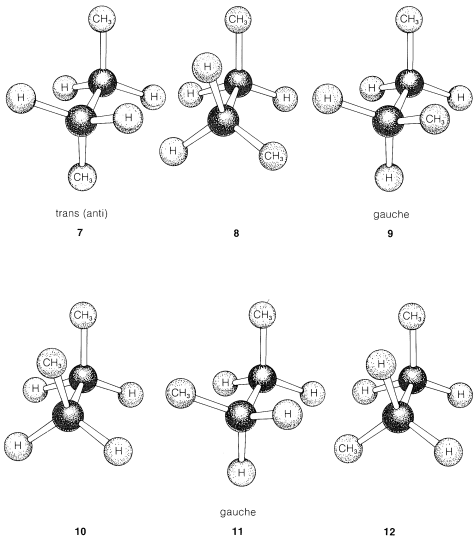
In butane, \(CH_3CH_2CH_2CH_3\), a \(360^\text{o}\) rotation about the central \(C-C\) bond allows the molecule to pass through three different eclipsed arrangements (\(8\), \(10\), \(12\)), and three different staggered arrangements (\(7\), \(9\), \(11\)), as shown in Figure 5-7. Experiment shows that butane favors the staggered form \(7\) in which the methyl groups are farthest apart. This form is called the anti (or trans) conformation (sometimes conformer), and \(63\%\) of the molecules of butane exist in this form at room temperature. The other two staggered forms \(9\) and \(11\) are called gauche (syn or skew) conformations and have a torsional angle of \(60^\text{o}\) between the two methyl groups. Forms \(9\) and \(11\) actually are nonidentical mirror images, but bond rotation is so rapid that the separate enantiomeric conformations cannot be isolated. The populations of the two gauche forms are equal at room temperature (\(18.5\%\) of each) so any optical rotation caused by one form is exactly canceled by an opposite rotation caused by the other.
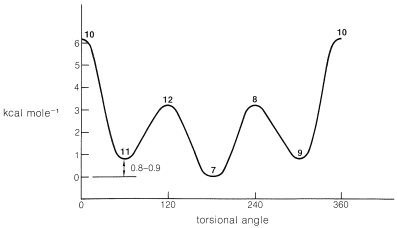
The populations of the eclipsed forms of butane, like the eclipsed forms of ethane, are small and represent energy maxima for the molecule as rotation occurs about the central \(C-C\) bond. The energy differences between the butane conformations are represented diagrammatically in Figure 5-8. The valleys correspond to staggered forms and the energy difference between the anti and gauche forms is \(0.8\)-\(0.9 \: \text{kcal mol}^{-1}\).
Pioneering work in the field of conformational analysis was contributed by O. Hassel (Norway) and D. R. H. Barton (Britain), for which they shared the Nobel Prize in chemistry in 1969. Hassel's work involved the physical determination of preferred conformations of small molecules, whereas Barton was the first to show the general importance of conformation to chemical reactivity. Study of conformations and conformational equilibria has direct application to explaining the extraordinary specificity exhibited by compounds of biological importance. The compounds of living systems are tailor-made to perform highly specific or even unique functions by virtue of their particular configurations and conformations.
\(^4\)This is by no means a trivial amount of energy - the difference in energy between the staggered and eclipsed forms of \(1 \: \text{mol}\) (\(30 \: \text{g}\)) of ethane being enough to heat \(30 \: \text{g}\) of water from \(0^\text{o}\) to \(100^\text{o}\).
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."
Template:HideTOC

