HW Solutions #9

UC Davis - Spring 2021
Chemistry 2C

Unit 1: Electrochemistry  ●  Unit 2: Coordination Chemistry  ●  Unit 3: Descriptive Chemistry  ●  Unit 4: Chemical Kinetics  ●  Unit 5: Nuclear Chemistry
  Agenda  ●  Textbook  ●  ADAPT  ●  Worksheets

Template:HideTOC

1. Answer the following questions based on the potential energy diagram shown here:

1. Does the graph represent an endothermic or exothermic reaction?
2. Label the position of the reactants, products, and activated complex.
3. Determine the heat of reaction, ΔH, (enthalpy change) for this reaction.
4. Determine the activation energy, E_a for this reaction.
5. How much energy is released or absorbed during the reaction?
6. How much energy is required for this reaction to occur?

A) The reaction is endothermic

B) Reactants are located on the flat portion to the left of the peak. Products are located on the flat portion to the right of the peak. The activated complex is located at the peak of the reaction diagram.

C) The enthalpy change is +50 kJ

D) The activation energy is 200 kJ

E) 50 kJ is absorbed in this reaction

F) An input of 200 kJ is required for this reaction to occur

Sean Gottlieb

2. Sketch a potential energy curve that is represented by the following values of ΔH and E_a. You may make up appropriate values for the y-axis (potential energy).

ΔH = -100 kJ and E_a = 20 kJ

Is this an endothermic or exothermic reaction?

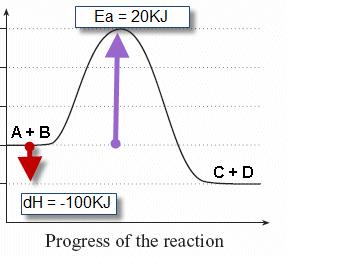
Its an exothermic reaction

3. Hydrogen gas and oxygen gas react to form water, but water can also be broken down into hydrogen and oxygen gas; we typically write a reaction that can be reversed this way, using the double arrow symbol ( or ↔):

2 H₂ + O₂ ↔ 2 H₂O

This reaction is exothermic in the forward direction:

2 H₂ + O₂ ↔ 2 H₂O + 285 kJ

but endothermic in the reverse direction:

2 H₂O + 285 kJ ↔ 2 H₂ + O₂

Consider a general reversible reaction such as:

A + B ↔ C + D

Given the following potential energy diagram for this reaction, determine ΔH and E_a for both the forward and reverse directions. Is the forward reaction endothermic or exothermic?

Solution:

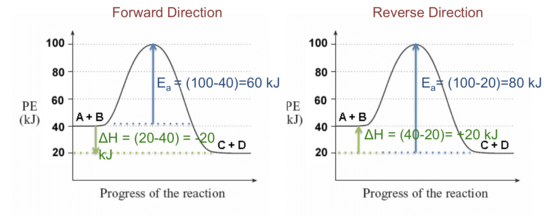
Activation Energy (E_a) is the difference in energy between the activated complex and the reactants as shown in the figure above. Large energy barriers separates the reactants and the products so that only very energetic molecules can pass over this barrier.

The forward reaction is exothermic.

~Diana Wong

4. Sketch a potential energy diagram for a general reaction

A + B ↔ C + D

Given that ΔH_reverse = -10 kJ and E_{a forward} = +40 kJ

ANSWER:

- John O.

5. Which one of the following reactions would you expect to be fastest at room temperature and why?

Pb^2+(aq) + 2 Cl^-(aq) → PbCl2 (s) Pb(s) + Cl2 (g) → PbCl2 (s)

We would expect the first reaction to be fastest at room temperature because both reactants are in the same phase. This will make collision between them more likely.

Sean Gottlieb

6. Consider the following reactions. Which do you predict will occur most rapidly at room conditions? Slowest?

C2H6 (g) + O2 (g) → 2 CO2 (g) + 3 H2O(g) Fastest Fe(s) + O2 (g) → Fe2O3 (s) Slowest H2O(l) + CO2 (g) → H2CO3 (g) 2 Fe^3+(aq) + Sn^2+(aq) → 2 Fe^2+(aq) + Sn^4+(aq)

7. Consider the following reaction that occurs between hydrochloric acid, HCl, and zinc metal:

HCl_(aq) + Zn_(s) → H_{2 (g)} + ZnCl_{2 (aq)}

Will this reaction occur fastest using a 6 M solution of HCl or a 0.5 M solution of HCl? Explain.

This reaction will occur the fastest using a 6M HCl solution. The reason for this can be explained in two ways:

1.) Rate = k[HCl(aq)]^m and since concentration is proportional to the rate, the higher the concentration (M) of HCl, the higher the rate of the reaction (M/min).

2.) The rate of the reaction also depends on the collision frequency (the number of molecular collision per unit of time). For any reaction to occur from a collision between molecules, there must be a redistribution of energy for bond breakage, which usually occurs when two fast-moving molecules collide. These collision from fast moving molecules have enough energy to cross an activation energy barrier, the minimum energy that molecules must bring in order for a chemical reaction to occur. Therefore, a higher concentration of reactant increases the probability of molecular collision and thus, increasing the collision frequency and the rate of the reaction.

~Diana Wong

8. Again consider the reaction between hydrochloric acid and zinc. How will increasing the temperature affect the rate of the reaction? Explain.

Reaction rate will increase as temperature increases. Because the H₂ gas formed is stable, and also forms a different (gaseous) phase, this is not a very reversible reaction. If the reaction is not reversible then Le Chatelier's principle is not applicable. Increasing the temperature will provide energy for the reaction to get past E_a and this will speed up the reaction. Even though the reaction is exothermic, it will not be pushed in the reverse direction, because the reaction is not reversible.

-John O.

9. Based on the following kinetic energy curves, which reaction will have a faster rate - A or B? Explain. Also, which reaction, A or B, would benefit most in terms of increased rate if the temperature of the system were increased?

A.
B.

The black line indicates the minimum kinetic energy required for a chemical reaction to occur. The rate of a reaction depends on the product of the collision frequency and the fraction of "activated" molecules. The fraction of activated molecules is greater in B since the minimum kinetic energy required for a likely chemical reaction is lower than in A. Thus, B will have a faster rate.

A would benefit the most by an increase in temperature since this would result in a shifted (to the right) and flatter curve as in T2 in Figure 14-8 in the text. Much more molecules would now become "activated". B would not benefit as much since a majority of the molecules already possess the minimum kinetic energy.

~Rachel

10. Phosgene, COCl₂, one of the poison gases used during World War I, is formed from chlorine and carbon monoxide. The mechanism is thought to proceed by:

step 1: Cl + CO → COCl step 2: COCl + Cl2 → COCl2 + Cl a. Write the overall reaction equation. b. Identify any reaction intermediates. c. Identify any catalysts.

A) CO + Cl₂ --> COCl₂

B) COCl is an intermediate

C) Cl is a catalyst

Sean Gottlieb

11.	We have typically been simplifying our potential energy curves somewhat; for multistep reactions, potential energy curves are more accurately shown with multiple peaks. Each peak represents the activated complex for an individual step. Consider the PE curve for a two-step reaction on the right:
	a. What is ΔH for the overall reaction? -20kJ b. What is ΔH for the first step of the reaction mechanism? 20kJ c. What is ΔH for the second step of the reaction mechanism? -40kJ d. What is ΔH for the overall reverse reaction? 20kJ e. What is Ea for the first step? 80kJ f. What is Ea for the second step? 40kJ g. Which is the rate-determing step - step 1 or step 2? How do you know? Step 1, due to the largest activation energy. h. What is Ea for the reverse of step 1? 60kJ i. Is the overall reaction endothermic or exothermic? Exothermic

-Erik

12. If phosphorous-32 emits a beta particle, an isotope of what element is formed.
(a) sulfur (b) chlorine (c) silicon (d) aluminum

13. What element is formed by the following nuclear fusion reaction?

First, figure out the elements formed in the nuclear fission reaction. These include fusion fragment (X) + neutron.

²₁H + ³₁H → ⁴₂X + ¹₀n

Second, figure out the element ^mass_protonX with mass=4 and proton=2.

(a) beryllium ⁹₄Be
(b) lithium ⁷₃Li
(c) helium ⁴₂He
(d) a new isotope of hydrogen

Based on all the possible given solution, He has a mass of 4 and 2 protons, and thus is element X

~Diana Wong

14. Complete the following nuclear equations and supply symbols or values for X and x:

1. ^x₈₈Ra → ⁴₂X + ²²²_xX
2. ¹⁴_xC → ^x_xN + ⁰_-1e
3. ^x_xNe → ¹⁹_xF + ⁰₊₁e
4. ⁷³_xAs + ⁰_-1e → ^x₃₂X
5. ¹⁷⁶_xLu → ^x_xX + ^x_-1e
6. ²³⁵_xU + ¹₀n → x¹₀n + ⁹⁴₃₆X + ¹³⁹_xX
7. ⁵⁹_xCo+ ²₁X → ⁶⁰_xCo+ ^x_xX
8. ¹⁹₉X + ¹_xH → ¹⁶₈X + ⁴_xX
9. ¹⁶₈X + ²₁X → ^x_xX + ⁴_xX
10. ²⁶_xMg + ¹₀X → ⁴_xHe + ^x_xX

1. ²²⁶₈₈Ra → ⁴₂He + ²²²₈₆Rn
2. ¹⁴₆C → ¹⁴₇N + ⁰_-1e
3. ¹⁹₁₀Ne → ¹⁹₉F + ⁰₊₁e
4. ⁷³₃₃As + ⁰_-1e → ⁷³₃₂Ge
5. ¹⁷⁶₇₁Lu → ¹⁷⁶₇₂Hf + ⁰_-1e
6. ²³⁵₉₂U + ¹₀n → 3 ¹₀n + ⁹⁴₃₆Kr + ¹³⁹₅₆Ba
7. ⁵⁹₂₇Co+ ²₁H → ⁶⁰₂₇Co+ ¹₁H
8. ¹⁹₉F + ¹₁H → ¹⁶₈O + ⁴₂He
9. ¹⁶₈O + ²₁H → ¹⁴₇N + ⁴₂He
10. ²⁶₁₂Mg + ¹₀n → ⁴₂He + ²³₁₀Ne

--- Hao

Homework#15. Write equations for each of the following nuclear processes:

1. positron emission by ¹²⁰₅₁Sb
2. electron emission by ³⁵₁₆S
3. α-particle emission by ²²⁶₈₈Ra
4. electron capture by ⁷₄Be.

1. ¹²⁰₅₁Sb → ¹²⁰₅₀Sn +⁰₊₁e
   
2. ³⁵₁₆S → ³⁵₁₇Cl + ⁰_-1e
   
3. ²²⁶₈₈Ra → ²²²₈₆Rn + ⁴₂He
   
4. ⁷₄Be + ⁰_-1e → ⁷₃Li
   

--- Hao

16. The decay of ²³⁴₉₂U ultimately leads to ²⁰⁶₈₂Pb. The process proceeds via the sequence of α and β decay steps: α, α, α ,α, α, β^-,β^-, α, β^-, β^-, α. Write the symbol for each of the isotopes produced in the decay chain.

²³⁴₉₂U --> ⁴₂He + ²³⁰₉₀Th

²³⁰₉₀Th --> ⁴₂He + ²²⁶₈₈Ra

²²⁶₈₈Ra --> ⁴₂He + ²²²₈₆Rn

²²²₈₆Rn --> ⁴₂He + ²¹⁸₈₄Po

²¹⁸₈₄Po --> ⁴₂He + ²¹⁴₈₂Pb

²¹⁴₈₂Pb --> ⁰_-1β + ²¹⁴₈₃Bi

²¹⁴₈₃Bi --> ⁰_-1β + ²¹⁴₈₄Po

²¹⁴₈₄Po --> ⁴₂He + ²¹⁰₈₂Pb

²¹⁰₈₂Pb--> ⁰_-1β + ²¹⁰₈₃Bi

²¹⁰₈₃Bi--> ⁰_-1β + ²¹⁰₈₄Po

²¹⁰₈₄Po --> ⁴₂He + ²⁰⁶₈₂Pb

%3ark#

17. (a) The heat of combustion of CH₄(g) is -495.0 kJ mole^-1. Calculate the mass equivalent of this energy in grams. (b) When ¹⁴C decays to ¹⁴₇N + ⁰_-1e, a mass loss of 0.000168 amu occurs. How many moles of CH₄(g) would have to be burned to produce the same amount of energy as would be produced from the decay of 1 mole of ¹⁴C?

18. When two ¹₁H nuclei and two neutrons combine to form ⁴₂He, the mass of the product helium nuclei is not the same as the sum of the masses of the reactant particles. Calculate the energy, in joules per mole of helium atoms, that is equivalent to the change in mass during the reaction. lf the energy per helium atom were released as a single photon, what would be its wavelength? How does this wavelength compare with the approximate radius of the helium nucleus?

mass_proton=1.6726*10^-27 kg

mass_neutron=1.6749*^10-27 kg

calculated mass_nucleus=6.6950*10^-27 kg

actual mass_nucleus=4.0026 amu=6.6464*10^-27 kg

mass_difference=calculated mass_nucleus-actual mass_nucleus=4.86*10^-29 kg

E=mc²=(4.86*10^-29 kg)*(2.998*10⁸ m/s)²=4.368*10^-12 J

E_mol=E*N_a=4.368*10-12 J * 6.022*10²³ mol^-1 = 2.631*10¹² J/mol

v_photon=E/h=(4.368*10^-12 J)/(6.626*10^-34 J*s) = 6.592*10²¹ s^-1

WL_photon=c_light/v_photon=4.548*10^-14 m ~ 45 fm

The radius of a helium-4 nucleus is 1.7 fm. The wavelength is about a factor of 25 larger than the radius.

-Erik

19. Calculate the binding energy per nucleon for the following nuclear species:

1. ¹²₆C (m = 12.0000 amu)
2. ³⁷₁₇Cl (m = 36.96590 amu)
3. ²⁰⁸₈₂Pb (m = 207.9766 amu)
4. ³²₁₆S (m = 31.97207 amu)
5. ¹⁶₈O (m = 15.99491 amu)