21.3: Radioactive Decay

Learning Objectives

By the end of this section, you will be able to:

• Recognize common modes of radioactive decay
• Identify common particles and energies involved in nuclear decay reactions
• Write and balance nuclear decay equations
• Calculate kinetic parameters for decay processes, including half-life
• Describe common radiometric dating techniques

Following the somewhat serendipitous discovery of radioactivity by Becquerel, many prominent scientists began to investigate this new, intriguing phenomenon. Among them were Marie Curie (the first woman to win a Nobel Prize, and the only person to win two Nobel Prizes in different sciences—chemistry and physics), who was the first to coin the term “radioactivity,” and Ernest Rutherford (of gold foil experiment fame), who investigated and named three of the most common types of radiation. During the beginning of the twentieth century, many radioactive substances were discovered, the properties of radiation were investigated and quantified, and a solid understanding of radiation and nuclear decay was developed.

The spontaneous change of an unstable nuclide into another is radioactive decay. The unstable nuclide is called the parent nuclide; the nuclide that results from the decay is known as the daughter nuclide. The daughter nuclide may be stable, or it may decay itself. The radiation produced during radioactive decay is such that the daughter nuclide lies closer to the band of stability than the parent nuclide, so the location of a nuclide relative to the band of stability can serve as a guide to the kind of decay it will undergo (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): A nucleus of uranium-238 (the parent nuclide) undergoes \(α\) decay to form thorium-234 (the daughter nuclide). The alpha particle removes two protons (green) and two neutrons (gray) from the uranium-238 nucleus.

Link to Learning

Although the radioactive decay of a nucleus is too small to see with the naked eye, we can indirectly view radioactive decay in an environment called a cloud chamber. Click here to learn about cloud chambers and to view an interesting Cloud Chamber Demonstration from the Jefferson Lab.

Types of Radioactive Decay

Ernest Rutherford’s experiments involving the interaction of radiation with a magnetic or electric field (Figure \(\PageIndex{2}\)) helped him determine that one type of radiation consisted of positively charged and relatively massive \(α\) particles; a second type was made up of negatively charged and much less massive \(β\) particles; and a third was uncharged electromagnetic waves, γ rays. We now know that \(α\) particles are high-energy helium nuclei, \(β\) particles are high-energy electrons, and γ radiation compose high-energy electromagnetic radiation. We classify different types of radioactive decay by the radiation produced.

Figure \(\PageIndex{2}\): Alpha particles, which are attracted to the negative plate and deflected by a relatively small amount, must be positively charged and relatively massive. Beta particles, which are attracted to the positive plate and deflected a relatively large amount, must be negatively charged and relatively light. Gamma rays, which are unaffected by the electric field, must be uncharged.

Alpha (\(α\)) decay is the emission of an \(α\) particle from the nucleus. For example, polonium-210 undergoes \(α\) decay:

\[\ce{_{84}^{210} Po ->_{2}^{4} He +_{82}^{206} Pb} \nonumber \]

or

\[\ce{_{84}^{210} Po ->_{2}^{4} \alpha +_{82}^{206} Pb} \nonumber \]

Alpha decay occurs primarily in heavy nuclei (\(A > 200\), \(Z > 83\)). Because the loss of an \(α\) particle gives a daughter nuclide with a mass number four units smaller and an atomic number two units smaller than those of the parent nuclide, the daughter nuclide has a larger n:p ratio than the parent nuclide. If the parent nuclide undergoing \(α\) decay lies below the band of stability (refer to Figure 21.2), the daughter nuclide will lie closer to the band.

Beta (\(β\)) decay is the emission of an electron (i.e., a \(\beta\) particle) from a nucleus. Iodine-131 is an example of a nuclide that undergoes \(β\) decay:

\[\ce{_{53}^{131} I ->_{-1}^0 e +_{54}^{131} Xe} \nonumber \]

or

\[ \ce{_{53}^{131} I ->_{-1}^0 \beta +_{54}^{131} Xe} \nonumber \]

Beta decay, which can be thought of as the conversion of a neutron into a proton and a \(β\) particle, is observed in nuclides with a large n:p ratio. The beta particle (electron) emitted is from the atomic nucleus and is not one of the electrons surrounding the nucleus. Such nuclei lie above the band of stability. Emission of an electron does not change the mass number of the nuclide but does increase the number of its protons and decrease the number of its neutrons. Consequently, the n:p ratio is decreased, and the daughter nuclide lies closer to the band of stability than did the parent nuclide.

Gamma emission (\(γ\) emission) is observed when a nuclide is formed in an excited state and then decays to its ground state with the emission of a \(γ\) ray, a quantum of high-energy electromagnetic radiation. The presence of a nucleus in an excited state is often indicated by an asterisk (*). Cobalt-60 emits \(γ\) radiation and is used in many applications including cancer treatment:

\[ \ce{_{27}^{60} Co^{*} ->_0^0 \gamma +_{27}^{60} Co} \nonumber \]

There is no change in mass number or atomic number during the emission of a \(γ\) ray unless the \(γ\) emission accompanies one of the other modes of decay.

Positron emission (\(β^{+}\) decay) is the emission of a positron from the nucleus. Oxygen-15 is an example of a nuclide that undergoes positron emission:

\[\ce{_{8}^{15} O ->_{+1}^0 e +_7^{15} N} \nonumber \]

or

\[\ce{_{8}^{15} O ->_{+1}^0 \beta +_7^{15} N} \nonumber \]

Positron emission is observed for nuclides in which the n:p ratio is low. These nuclides lie below the band of stability. Positron decay is the conversion of a proton into a neutron with the emission of a positron. The n:p ratio increases, and the daughter nuclide lies closer to the band of stability than did the parent nuclide.

Electron capture occurs when one of the inner electrons in an atom is captured by the atom’s nucleus. For example, potassium-40 undergoes electron capture:

\[\ce{_{19}^{40} K +_{-1}^0 e ->_{18}^{40} Ar} \nonumber \]

Electron capture occurs when an inner shell electron combines with a proton and is converted into a neutron. The loss of an inner shell electron leaves a vacancy that will be filled by one of the outer electrons. As the outer electron drops into the vacancy, it will emit energy. In most cases, the energy emitted will be in the form of an X-ray. Like positron emission, electron capture occurs for “proton-rich” nuclei that lie below the band of stability. Electron capture has the same effect on the nucleus as does positron emission: The atomic number is decreased by one and the mass number does not change. This increases the n:p ratio, and the daughter nuclide lies closer to the band of stability than did the parent nuclide. Whether electron capture or positron emission occurs is difficult to predict. The choice is primarily due to kinetic factors, with the one requiring the smaller activation energy being the one more likely to occur.

Figure \(\PageIndex{3}\) summarizes these types of decay, along with their equations and changes in atomic and mass numbers.

Figure \(\PageIndex{3}\): This table summarizes the type, nuclear equation, representation, and any changes in the mass or atomic numbers for various types of decay.

Chemistry in Everyday Life: PET Scan

Positron emission tomography (PET) scans use radiation to diagnose and track health conditions and monitor medical treatments by revealing how parts of a patient’s body function (Figure \(\PageIndex{4}\)). To perform a PET scan, a positron-emitting radioisotope is produced in a cyclotron and then attached to a substance that is used by the part of the body being investigated. This “tagged” compound, or radiotracer, is then put into the patient (injected via IV or breathed in as a gas), and how it is used by the tissue reveals how that organ or other area of the body functions.

Figure \(\PageIndex{4}\): A PET scanner (a) uses radiation to provide an image of how part of a patient’s body functions. The scans it produces can be used to image a healthy brain (b) or can be used for diagnosing medical conditions such as Alzheimer’s disease (c). (credit a: modification of work by Jens Maus)

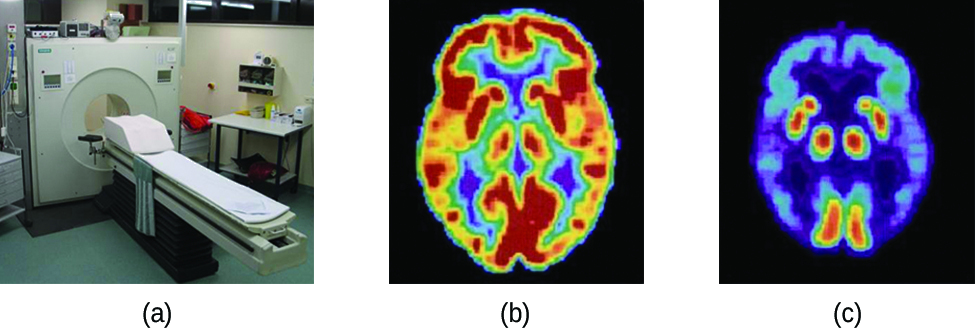
For example, F-18 is produced by proton bombardment of \(\ce{^{^18}O}\)

\[\ce{_{8}^{18} O +_{1}^{1} p ->_{9}^{18} F +_{0}^{1} n} \nonumber \]

and incorporated into a glucose analog called fludeoxyglucose (FDG). How FDG is used by the body provides critical diagnostic information; for example, since cancers use glucose differently than normal tissues, FDG can reveal cancers. The \(\ce{^{18}F}\) emits positrons that interact with nearby electrons, producing a burst of gamma radiation. This energy is detected by the scanner and converted into a detailed, three-dimensional, color image that shows how that part of the patient’s body functions. Different levels of gamma radiation produce different amounts of brightness and colors in the image, which can then be interpreted by a radiologist to reveal what is going on. PET scans can detect heart damage and heart disease, help diagnose Alzheimer’s disease, indicate the part of a brain that is affected by epilepsy, reveal cancer, show what stage it is, and how much it has spread, and whether treatments are effective. Unlike magnetic resonance imaging and X-rays, which only show how something looks, the big advantage of PET scans is that they show how something functions. PET scans are now usually performed in conjunction with a computed tomography scan.

Radioactive Decay Series

The naturally occurring radioactive isotopes of the heaviest elements fall into chains of successive disintegrations, or decays, and all the species in one chain constitute a radioactive family, or radioactive decay series. Three of these series include most of the naturally radioactive elements of the periodic table. They are the uranium series, the actinide series, and the thorium series. The neptunium series is a fourth series, which is no longer significant on the earth because of the short half-lives of the species involved. Each series is characterized by a parent (first member) that has a long half-life and a series of daughter nuclides that ultimately lead to a stable end-product—that is, a nuclide on the band of stability (Figure \(\PageIndex{5}\)). In all three series, the end-product is a stable isotope of lead. The neptunium series, previously thought to terminate with bismuth-209, terminates with thallium-205.

Figure \(\PageIndex{5}\): Uranium-238 undergoes a radioactive decay series consisting of 14 separate steps before producing stable lead-206. This series consists of eight \(α\) decays and six \(β\) decays.

Radioactive Half-Lives

Radioactive decay follows first-order kinetics. Since first-order reactions have already been covered in detail in the kinetics chapter, we will now apply those concepts to nuclear decay reactions. Each radioactive nuclide has a characteristic, constant half-life (\(t_{1/2}\)), the time required for half of the atoms in a sample to decay. An isotope’s half-life allows us to determine how long a sample of a useful isotope will be available, and how long a sample of an undesirable or dangerous isotope must be stored before it decays to a low-enough radiation level that is no longer a problem.

For example, coba source, since half of the nuclei decay every 5.27 years, both the amount of material and the intensity of the radiation emitted is cut in half every 5.27 years. (Note that for a given substance, the intensity of radiation that it produces is directly proportional to the rate of decay of the substance and the amount of the substance.) This is as expected for a process following first-order kinetics. Thus, a cobalt-60 source that is used for cancer treatment must be replaced regularly to continue to be effective.

Figure \(\PageIndex{6}\): For cobalt-60, which has a half-life of 5.27 years, 50% remains after 5.27 years (one half-life), 25% remains after 10.54 years (two half-lives), 12.5% remains after 15.81 years (three half-lives), and so on.

Since nuclear decay follows first-order kinetics, we can adapt the mathematical relationships used for first-order chemical reactions. We generally substitute the number of nuclei, \(N\), for the concentration. If the rate is stated in nuclear decays per second, we refer to it as the activity of the radioactive sample. The rate for radioactive decay is:

\[\text{decay rate} = λN \nonumber \]

with \(λ\) = the decay constant for the particular radioisotope.

The decay constant, \(λ\), which is the same as a rate constant discussed in the kinetics chapter. It is possible to express the decay constant in terms of the half-life, \(t_{1/2}\):

\[\lambda=\dfrac{\ln 2}{t_{1 / 2}}=\dfrac{0.693}{t_{1 / 2}} \nonumber \]

or

\[t_{1 / 2}=\dfrac{\ln 2}{\lambda}=\dfrac{0.693}{\lambda} \nonumber \]

The first-order equations relating amount, \(N\), and time are:

\[N_t=N_0 e^{-\lambda t} \label{firstorder} \]

or

\[t=-\frac{1}{\lambda} \ln \left(\frac{N_t}{N_0}\right) \nonumber \]

Example \(\PageIndex{1}\): Rates of Radioactive Decay

\(\ce{^{60}_{27}Co}\) decays with a half-life of 5.27 years to produce \(\ce{^{60}_{28}Co}\)

1. What is the decay constant for the radioactive disintegration of cobalt-60?
2. Calculate the fraction of a sample of the \(\ce{^{60}_{27}Co}\) isotope that will remain after 15 years.
3. How long does it take for a sample of \(\ce{^{60}_{27}Co}\) to disintegrate to the extent that only 2.0% of the original amount remains?

Solution

(a) The value of the rate constant is given by:

\[\lambda=\frac{\ln 2}{t_{1 / 2}}=\frac{0.693}{5.27 y }=0.132 y^{-1} \nonumber \]

(b) The fraction of \(\ce{^{60}_{27}Co}\) that is left after time \(t\) is given by \(\frac{N_t}{N_0}\). Rearranging the first-order relationship in Equation \ref{firstorder} (\(N_t = N_0e^{–λt}\) to solve for this ratio yields:

\[\frac{N_t}{N_0}=e^{-\lambda t}=e^{-(0.132 / \text{y} )(15 \, \text{y} )}=0.138 \nonumber \]

The fraction of \(\ce{^{60}_{27}Co}\) that will remain after 15.0 years is 0.138. Or put another way, 13.8% of the original \(\ce{^{60}_{27}Co}\) present will remain after 15 years.

(c) 2.00% of the original amount of \(\ce{^{60}_{27}Co}\) is equal to 0.0200 N₀. Substituting this into the equation for time for first-order kinetics, we have:

\[t=-\frac{1}{\lambda} \ln \left(\frac{N_t}{N_0}\right)=-\frac{1}{0.132\, \text{y}^{-1}} \ln \left(\frac{0.0200 \times N_0}{N_0}\right)=29.6 y \nonumber \]

Exercise \(\PageIndex{1}\)

Radon-222, \(\ce{^{222}_{86}Rn}\) has a half-life of 3.823 days. How long will it take a sample of radon-222 with a mass of 0.750 g to decay into other elements, leaving only 0.100 g of radon-222?

Answer

11.1 days

Because each nuclide has a specific number of nucleons, a particular balance of repulsion and attraction, and its own degree of stability, the half-lives of radioactive nuclides vary widely. For example: the half-life of \(\ce{^{209}_{83}Bi}\) is \(1.9 \times 10^{19}\) years; \(\ce{^{239}_{94}Ra}\) is 24,000 years; \(\ce{^{222}_{86}Rn}\) is 3.82 days; and element-111 (Rg for roentgenium) is \(1.5 \times 10^{–3}\) seconds. The half-lives of a number of radioactive isotopes important to medicine are shown in Table \(\PageIndex{1}\), and others are listed in Appendix M.

Table \(\PageIndex{1}\): Half-lives of Radioactive Isotopes Important to Medicine

Type^1	Decay Mode	Half-Life	Uses
F-18	β^+ decay	110. minutes	PET scans
Co-60	β decay, γ decay	5.27 years	cancer treatment
Tc-99m	γ decay	8.01 hours	scans of brain, lung, heart, bone
I-131	β decay	8.02 days	thyroid scans and treatment
Tl-201	electron capture	73 hours	heart and arteries scans; cardiac stress tests

Radiometric Dating

Several radioisotopes have half-lives and other properties that make them useful for purposes of “dating” the origin of objects such as archaeological artifacts, formerly living organisms, or geological formations. This process is radiometric dating and has been responsible for many breakthrough scientific discoveries about the geological history of the earth, the evolution of life, and the history of human civilization. We will explore some of the most common types of radioactive dating and how the particular isotopes work for each type.

Radioactive Dating Using Carbon-14

The radioactivity of carbon-14 provides a method for dating objects that were a part of a living organism. This method of radiometric dating, which is also called radiocarbon dating or carbon-14 dating, is accurate for dating carbon-containing substances that are up to about 30,000 years old, and can provide reasonably accurate dates up to a maximum of about 50,000 years old.

Naturally occurring carbon consists of three isotopes: \(\ce{^{12}_{6}C}\) which constitutes about 99% of the carbon on earth; \(\ce{^{13}_6C}\), about 1% of the total; and trace amounts of \(\ce{^{14}_6C}\). Carbon-14 forms in the upper atmosphere by the reaction of nitrogen atoms with neutrons from cosmic rays in space:

\[\ce{_{7}^{14} N +_{0}^{1}n ->_{6}^{14}C + _{1}^{1} H} \nonumber \]

All isotopes of carbon react with oxygen to produce \(\ce{CO2}\) molecules. The ratio of \(\ce{^{14}_{6}CO2}\) to \(\ce{^{12}_{6}CO2}\) depends on the ratio of \(\ce{^{14}_{6}CO}\) to \(\ce{^{12}_{6}CO}\) in the atmosphere. The natural abundance of \(\ce{^{14}_{6}CO}\) in the atmosphere is approximately 1 part per trillion; until recently, this has generally been constant over time, as seen is gas samples found trapped in ice. The incorporation of \(\ce{^{14}_{6}CO2}\) and \(\ce{^{14}_{6}CO2}\) into plants is a regular part of the photosynthesis process, which means that the \(\ce{^{14}_{6}C} : \ce{^{12}_{6}C}\) ratio found in a living plant is the same as the \(\ce{^{14}_{6}C} : \ce{^{12}_{6}C}\) ratio in the atmosphere. But when the plant dies, it no longer traps carbon through photosynthesis. Because \(\ce{^{12}_{6}C}\) is a stable isotope and does not undergo radioactive decay, its concentration in the plant does not change. However, carbon-14 decays by \(β\) emission with a half-life of 5730 years:

\[\ce{_{6}^{14} C ->_{7}^{14} N +_{-1}^0 e} \nonumber \]

Thus, the ratio gradually decreases after the plant dies. The decrease in the ratio with time provides a measure of the time that has elapsed since the death of the plant (or other organism that ate the plant). Figure \(\PageIndex{7}\): visually depicts this process.

Figure \(\PageIndex{7}\): Along with stable carbon-12, radioactive carbon-14 is taken in by plants and animals, and remains at a constant level within them while they are alive. After death, the C-14 decays and the C-14:C-12 ratio in the remains decreases. Comparing this ratio to the C-14:C-12 ratio in living organisms allows us to determine how long ago the organism lived (and died).

For example, with the half-life of being 5730 years, if the ratio in a wooden object found in an archaeological dig is half what it is in a living tree, this indicates that the wooden object is 5730 years old. Highly accurate determinations of ratios can be obtained from very small samples (as little as a milligram) by the use of a mass spectrometer.

Link to Learning

Visit this website to perform simulations of radiometric dating.

Example \(\PageIndex{2}\): Radiocarbon Dating

A tiny piece of paper (produced from formerly living plant matter) taken from the Dead Sea Scrolls has an activity of 10.8 disintegrations per minute per gram of carbon. If the initial C-14 activity was 13.6 disintegrations/min/g of C, estimate the age of the Dead Sea Scrolls.

Solution

The rate of decay (number of disintegrations/minute/gram of carbon) is proportional to the amount of radioactive C-14 left in the paper, so we can substitute the rates for the amounts, \(N\), in the relationship:

\[t=-\frac{1}{\lambda} \ln \left(\frac{N_t}{N_0}\right) \longrightarrow t=-\frac{1}{\lambda} \ln \left(\frac{\text { Rate }_t}{\text { Rate }_0}\right) \nonumber \]

where the subscript 0 represents the time when the plants were cut to make the paper, and the subscript t represents the current time.

The decay constant can be determined from the half-life of C-14, 5730 years:

\[\lambda=\frac{\ln 2}{t_{1 / 2}}=\frac{0.693}{5730 \,\text{y}}=1.21 \times 10^{-4}\, \text{y}^{-1} \nonumber \]

Substituting and solving, we have:

\[t=-\frac{1}{\lambda} \ln \left(\frac{\text { Rate }_t}{\text { Rate }_0}\right) = -\frac{1}{1.21 \times 10^{-4}\, \text{y}^{-1}} \ln \left(\frac{10.8 \, \cancel{ \text{dis} / \text{min} / \text{g}\, \ce{C}} }{13.6 \, \cancel{ \text{dis} / \text{min} / \text{g}\, \ce{C}} }\right)=1910\, \text{y} \nonumber \]

Therefore, the Dead Sea Scrolls are approximately 1900 years old (Figure \(\PageIndex{8}\)).

Figure \(\PageIndex{8}\): Carbon-14 dating has shown that these pages from the Dead Sea Scrolls were written or copied on paper made from plants that died between 100 BC and AD 50.

Exercise \(\PageIndex{1}\)

More accurate dates of the reigns of ancient Egyptian pharaohs have been determined recently using plants that were preserved in their tombs. Samples of seeds and plant matter from King Tutankhamun’s tomb have a C-14 decay rate of 9.07 disintegrations/min/g of C. How long ago did King Tut’s reign come to an end?

Answer

about 3350 years ago, or approximately 1340 BC

There have been some significant, well-documented changes to the \(\ce{^{14}_{6}C} : \ce{^{12}_{6}C}\) ratio. The accuracy of a straightforward application of this technique depends on the \(\ce{^{14}_{6}C} : \ce{^{12}_{6}C}\) ratio in a living plant being the same now as it was in an earlier era, but this is not always valid. Due to the increasing accumulation of \(\ce{CO2}\) molecules (largely \(\ce{^{12}_{6}C}\)) in the atmosphere caused by combustion of fossil fuels (in which essentially all of the \(\ce{^{14}_{6}C}\) has decayed), the ratio of \(\ce{^{14}_{6}C} : \ce{^{12}_{6}C}\) in the atmosphere may be changing. This manmade increase in \(\ce{^{12}_{6}C}\) in the atmosphere causes the \(\ce{^{14}_{6}C} : \ce{^{12}_{6}C}\) ratio to decrease, and this in turn affects the ratio in currently living organisms on the earth. Fortunately, however, we can use other data, such as tree dating via examination of annual growth rings, to calculate correction factors. With these correction factors, accurate dates can be determined. In general, radioactive dating only works for about 10 half-lives; therefore, the limit for carbon-14 dating is about 57,000 years.

Radioactive Dating Using Nuclides Other than Carbon-14

Radioactive dating can also use other radioactive nuclides with longer half-lives to date older events. For example, uranium-238 (which decays in a series of steps into lead-206) can be used for establishing the age of rocks (and the approximate age of the oldest rocks on earth). Since U-238 has a half-life of 4.5 billion years, it takes that amount of time for half of the original U-238 to decay into Pb-206. In a sample of rock that does not contain appreciable amounts of Pb-208, the most abundant isotope of lead, we can assume that lead was not present when the rock was formed. Therefore, by measuring and analyzing the ratio of U-238:Pb-206, we can determine the age of the rock. This assumes that all of the lead-206 present came from the decay of uranium-238. If there is additional lead-206 present, which is indicated by the presence of other lead isotopes in the sample, it is necessary to make an adjustment. Potassium-argon dating uses a similar method. K-40 decays by positron emission and electron capture to form Ar-40 with a half-life of 1.25 billion years. If a rock sample is crushed and the amount of Ar-40 gas that escapes is measured, determination of the Ar-40:K-40 ratio yields the age of the rock. Other methods, such as rubidium-strontium dating (Rb-87 decays into Sr-87 with a half-life of 48.8 billion years), operate on the same principle. To estimate the lower limit for the earth’s age, scientists determine the age of various rocks and minerals, making the assumption that the earth is older than the oldest rocks and minerals in its crust. As of 2014, the oldest known rocks on earth are the Jack Hills zircons from Australia, found by uranium-lead dating to be almost 4.4 billion years old.

Example \(\PageIndex{3}\): Radioactive Dating of Rocks

An igneous rock contains \(9.58 \times 10^{–5} \, \text{g}\) of U-238 and \(2.51 \times 10^{–5} \, \text{g}\) of Pb-206, and much, much smaller amounts of Pb-208. Determine the approximate time at which the rock formed.

Solution

The sample of rock contains very little Pb-208, the most common isotope of lead, so we can safely assume that all the Pb-206 in the rock was produced by the radioactive decay of U-238. When the rock formed, it contained all of the U-238 currently in it, plus some U-238 that has since undergone radioactive decay.

The amount of U-238 currently in the rock is:

\[9.58 \times 10^{-5}\, \cancel{\text{g}\, \ce{U}} \times\left(\frac{1\, \text{mol}\, \ce{U} }{238\, \cancel{\text{g}\, \ce{U}}}\right)=4.03 \times 10^{-7} \, \text{mol}\, \ce{U} \nonumber \]

Because when one mole of U-238 decays, it produces one mole of Pb-206, the amount of U-238 that has undergone radioactive decay since the rock was formed is:

\[2.51 \times 10^{-5}\, \cancel{ \text{g}\, \ce{Pb}} \times\left(\frac{1\, \bcancel{\text{mol}\, \ce{Pb}} }{206\, \cancel{ \text{g}\, \ce{Pb}} }\right) \times\left(\frac{1\, \text{mol}\, \ce{U}}{1\, \bcancel{\text{mol}\, \ce{Pb}} }\right)=1.22 \times 10^{-7}\, \text{mol}\, \ce{U} \nonumber \]

The total amount of U-238 originally present in the rock is therefore:

\[4.03 \times 10^{-7}\, \text{mol}\, \ce{U} + 1.22 \times 10^{-7}\, \text{mol}\, \ce{U} = 5.25 \times 10^{-7}\, \text{mol}\, \ce{U} \nonumber \]

The amount of time that has passed since the formation of the rock is given by:

\[t=-\frac{1}{\lambda} \ln \left(\frac{N_t}{N_0}\right) \nonumber \]

with \(N_0\) representing the original amount of U-238 and \(N_t\) representing the present amount of U-238.

U-238 decays into Pb-206 with a half-life of \(4.5 \times 10^9\, \text{y}\), so the decay constant \(λ\) is:

\[\lambda=\frac{\ln 2}{t_{1 / 2}}=\frac{0.693}{4.5 \times 10^9\, \text{y} }=1.54 \times 10^{-10} \, \text{y}^{-1} \nonumber \]

Substituting and solving, we have:

\[t=-\frac{1}{1.54 \times 10^{-10}\, \text{y}^{-1}} \ln \left(\frac{4.03 \times 10^{-7} \, \cancel{\text{mol}\, \ce{U}}}{5.25 \times 10^{-7} \, \cancel{\text{mol}\, \ce{U}}}\right)=1.7 \times 10^9 \, \text{y} \nonumber \]

Therefore, the rock is approximately 1.7 billion years old.

Exercise \(\PageIndex{1}\)

A sample of rock contains \(6.14 \times 10^{–4}\) g of Rb-87 and \(3.51 \times 10^{–5} g\) of Sr-87. Calculate the age of the rock. (The half-life of the \(β\) decay of Rb-87 is \(4.7 \times 10^{10}\, \text{y}\).)

Answer

3.7 10⁹ y

Footnotes

• 1The “m” in Tc-99m stands for “metastable,” indicating that this is an unstable, high-energy state of Tc-99. Metastable isotopes emit γ radiation to rid themselves of excess energy and become (more) stable.