14.7: Acid-Base Titrations

Learning Objectives

• Interpret titration curves for strong and weak acid-base systems
• Compute sample pH at important stages of a titration
• Explain the function of acid-base indicators

As seen in the chapter on the stoichiometry of chemical reactions, titrations can be used to quantitatively analyze solutions for their acid or base concentrations. In this section, we will explore the changes in the concentrations of the acidic and basic species present in a solution during the process of a titration.

Titration Curves

Previously, when we studied acid-base reactions in solution, we focused only on the point at which the acid and base were stoichiometrically equivalent. No consideration was given to the pH of the solution before, during, or after the neutralization.

Example \(\PageIndex{1}\): Calculating pH for Titration Solutions: Strong Acid/Strong Base

A titration is carried out for 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M of a strong base NaOH the titration curve is shown in Figure \(\PageIndex{1}\). Calculate the pH at these volumes of added base solution:

1. 0.00 mL
2. 12.50 mL
3. 25.00 mL
4. 37.50 mL

Solution

Since HCl is a strong acid, we can assume that all of it dissociates. The initial concentration of H₃O⁺ is \(\ce{[H3O+]_0}=0.100\:M\). When the base solution is added, it also dissociates completely, providing OH⁻ ions. The H₃O⁺ and OH⁻ ions neutralize each other, so only those of the two that were in excess remain, and their concentration determines the pH. Thus, the solution is initially acidic (pH < 7), but eventually all the hydronium ions present from the original acid are neutralized, and the solution becomes neutral. As more base is added, the solution turns basic.

The total initial amount of the hydronium ions is:

\[\mathrm{n(H^+)_0=[H_3O^+]_0×0.02500\: L=0.002500\: mol} \nonumber \]

Once X mL of the 0.100-M base solution is added, the number of moles of the OH⁻ ions introduced is:

\[\mathrm{n(OH^-)_0=0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

The total volume becomes:

\[V=\mathrm{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

The number of moles of H₃O⁺ becomes:

\[\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0=0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

The concentration of H₃O⁺ is:

\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{V}=\dfrac{0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}} \nonumber \]

\[\mathrm{=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)-0.100\:\mathit{M}×X\: mL}{25.00\: mL+X\: mL}} \nonumber \]

with the definition of \(\mathrm{pH}\):

\[\mathrm{pH=−\log([H_3O^+])} \label{phdef} \]

The preceding calculations work if \(\mathrm{n(H^+)_0-n(OH^-)_0>0}\) and so n(H⁺) > 0. When \(\mathrm{n(H^+)_0=n(OH^-)_0}\), the H₃O⁺ ions from the acid and the OH⁻ ions from the base mutually neutralize. At this point, the only hydronium ions left are those from the autoionization of water, and there are no OH⁻ particles to neutralize them. Therefore, in this case:

\[\ce{[H3O+]}=\ce{[OH- ]},\:\ce{[H3O+]}=K_\ce{w}=1.0\times 10^{-14};\:\ce{[H3O+]}=1.0\times 10^{-7} \nonumber \]

\[\mathrm{pH=-log(1.0\times 10^{-7})=7.00} \nonumber \]

Finally, when \(\mathrm{n(OH^-)_0>n(H^+)_0}\), there are not enough H₃O⁺ ions to neutralize all the OH⁻ ions, and instead of \(\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0}\), we calculate: \(\mathrm{n(OH^-)=n(OH^-)_0-n(H^+)_0}\)

In this case:

\[\mathrm{[OH^-]=\dfrac{n(OH^-)}{\mathit{V}}=\dfrac{0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)-0.002500\: mol}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}} \nonumber \]

\[\mathrm{=\dfrac{0.100\:\mathit{M}×X\: mL-0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL+X\: mL}} \nonumber \]

then using the definition of \(pOH\) and its relationship to \(pH\) in room temperature aqueous solutios (Equation \ref{phdef}):

\[\begin{align} pH &=14-pOH \nonumber \\&=14+\log([OH^-]) \nonumber\end{align} \nonumber \]

Let us now consider the four specific cases presented in this problem:

(a) X = 0 mL

\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{\mathit{V}}=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL}=0.1\:\mathit{M}} \nonumber \]

then using the definition of \(pH\) (Equation \ref{phdef}):

\[\begin{align} pH &= −\log(0.100) \nonumber \\ &= 1.000 \nonumber\end{align} \nonumber \]

(b) X = 12.50 mL

\[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{\mathit{V}}=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)-0.100\:\mathit{M}×12.50\: mL}{25.00\: mL+12.50\: mL}=0.0333\:\mathit{M}} \nonumber \]

then using the definition of \(pH\) (Equation \ref{phdef}):

\[ \begin{align} pH &= −\log(0.0333) \nonumber \\ &= 1.477 \nonumber\end{align} \nonumber \]

(c) X = 25.00 mL

Since the volumes and concentrations of the acid and base solutions are the same:

\[\mathrm{n(H^+)_0=n(OH^-)_0} \nonumber \]

and

\[pH = 7.000 \nonumber \]

as described earlier.

(d) X = 37.50 mL

In this case:

\[\mathrm{n(OH^-)_0>n(H^+)_0} \nonumber \]

\[\mathrm{[OH^-]=\dfrac{n(OH^-)}{\mathit{V}}=\dfrac{0.100\:\mathit{M}×35.70\: mL-0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL+37.50\: mL}=0.0200\:\mathit{M}} \nonumber \]

then using the definition of \(pH\) (Equation \ref{phdef}):

\[ \begin{align}[pH = 14 − pOH \nonumber\\ &= 14 + \log([OH^{−}]) \nonumber \\ &= 14 + \log(0.0200) \nonumber \\ &= 12.30 \nonumber \end{align} \nonumber \]

Exercise \(\PageIndex{1}\)

Calculate the pH for the strong acid/strong base titration between 50.0 mL of 0.100 M HNO₃(aq) and 0.200 M NaOH (titrant) at the listed volumes of added base:

1. 0.00 mL,
2. 15.0 mL,
3. 25.0 mL, and
4. 40.0 mL.

Answer a

0.00: 1.000

Answer b

15.0: 1.5111

Answer c

25.0: 7e. Do not delete this text first.

Answer d

40.0: 12.523

In Example \(\PageIndex{1}\), we calculated pH at four points during a titration. Table \(\PageIndex{1}\) shows a detailed sequence of changes in the pH of a strong acid and a weak acid in a titration with NaOH.

Table \(\PageIndex{1}\): pH Values in the Titrations of a Strong Acid with a Strong Base and of a Weak Acid with a Strong Base

Volume of 0.100 M NaOH Added (mL)	Moles of NaOH Added	pH Values 0.100 M HCl^1	pH Values 0.100 M \(CH_3CO_2H\)^2
0.0	0.0	1.00	2.87
5.0	0.00050	1.18	4.14
10.0	0.00100	1.37	4.57
15.0	0.00150	1.60	4.92
20.0	0.00200	1.95	5.35
22.0	0.00220	2.20	5.61
24.0	0.00240	2.69	6.13
24.5	0.00245	3.00	6.44
24.9	0.00249	3.70	7.14
25.0	0.00250	7.00	8.72
25.1	0.00251	10.30	10.30
25.5	0.00255	11.00	11.00
26.0	0.00260	11.29	11.29
28.0	0.00280	11.75	11.75
30.0	0.00300	11.96	11.96
35.0	0.00350	12.22	12.22
40.0	0.00400	12.36	12.36
45.0	0.00450	12.46	12.46
50.0	0.00500	12.52	12.52
Titration of 25.00 mL of 0.100 M HCl (0.00250 mol of HCI) with 0.100 M NaOH. Titration of 25.00 mL of 0.100 M CH3CO2H (0.00250 mol of CH3CO2H) with 0.100 M NaOH.

The simplest acid-base reactions are those of a strong acid with a strong base. Table \(\PageIndex{1}\) shows data for the titration of a 25.0-mL sample of 0.100 M hydrochloric acid with 0.100 M sodium hydroxide. The values of the pH measured after successive additions of small amounts of NaOH are listed in the first column of this table, and are graphed in Figure \(\PageIndex{1}\), in a form that is called a titration curve. The pH increases slowly at first, increases rapidly in the middle portion of the curve, and then increases slowly again. The point of inflection (located at the midpoint of the vertical part of the curve) is the equivalence point for the titration. It indicates when equivalent quantities of acid and base are present. For the titration of a strong acid with a strong base, the equivalence point occurs at a pH of 7.00 and the points on the titration curve can be calculated using solution stoichiometry (Table \(\PageIndex{1}\) and Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): (a) The titration curve for the titration of 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M NaOH (strong base) has an equivalence point of 7.00 pH. (b) The titration curve for the titration of 25.00 mL of 0.100 M CH₃CO₂H (weak acid) with 0.100 M NaOH (strong base) has an equivalence point of 8.72 pH.

Two graphs are shown. The first graph on the left is titled “Titration of Weak Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L).” Markings and vertical gridlines are provided every 5 units from 0 to 50. The vertical axis is labeled “p H” and is marked every 1 unis beginning at 0 extending to 14. A red curve is drawn on the graph which increases steadily from the point (0, 3) up to about (20, 5.5) after which the graph has a vertical section from (25, 7) up to (25, 11). The graph then levels off to a value of about 12.5 from about 40 m L up to 50 m L. The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 8.72.” The second graph on the right is titled “Titration of Strong Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L).” Markings and vertical gridlines are provided every 5 units from 0 to 50. The vertical axis is labeled “p H” and is marked every 1 units beginning at 0 extending to 14. A red curve is drawn on the graph which increases gradually from the point (0, 1) up to about (22.5, 2.2) after which the graph has a vertical section from (25, 4) up to nearly (25, 11). The graph then levels off to a value of about 12.4 from about 40 m L up to 50 m L. The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 7.00.”

The titration of a weak acid with a strong base (or of a weak base with a strong acid) is somewhat more complicated than that just discussed, but it follows the same general principles. Let us consider the titration of 25.0 mL of 0.100 M acetic acid (a weak acid) with 0.100 M sodium hydroxide and compare the titration curve with that of the strong acid. Table \(\PageIndex{1}\) gives the pH values during the titration, Figure \(\PageIndex{1b}\) shows the titration curve.

Although the initial volume and molarity of the acids are the same, there are important differences between the two titration curves. The titration curve for the weak acid begins at a higher value (less acidic) and maintains higher pH values up to the equivalence point. This is because acetic acid is a weak acid, which is only partially ionized. The pH at the equivalence point is also higher (8.72 rather than 7.00) due to the hydrolysis of acetate, a weak base that raises the pH:

\[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(l)+\ce{OH-}(aq) \nonumber \]

After the equivalence point, the two curves are identical because the pH is dependent on the excess of hydroxide ion in both cases.

Example \(\PageIndex{2}\): Titration of a Weak Acid with a Strong Base

The titration curve shown in Figure \(\PageIndex{1b}\) is for the titration of 25.00 mL of 0.100 M CH₃CO₂H with 0.100 M NaOH. The reaction can be represented as:

\[\ce{CH3CO2H + OH- ⟶ CH3CO2- + H2O} \nonumber \]

1. What is the initial pH before any amount of the NaOH solution has been added? K_a = 1.8 × 10⁻⁵ for CH₃CO₂H.
2. Find the pH after 25.00 mL of the NaOH solution have been added.
3. Find the pH after 12.50 mL of the NaOH solution has been added.
4. Find the pH after 37.50 mL of the NaOH solution has been added.

Solution

(a) Assuming that the dissociated amount is small compared to 0.100 M, we find that:

\[K_\ce{a}=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}}≈\ce{\dfrac{[H3O+]^2}{[CH3CO2H]_0}} \nonumber \]

and

\[\ce{[H3O+]}=\sqrt{K_\ce{a}×\ce{[CH3CO2H]}}=\sqrt{1.8\times 10^{-5}×0.100}=1.3\times 10^{-3} \nonumber \]

\[\mathrm{pH=-\log(1.3\times 10^{-3})=2.87} \nonumber \]

(b) After 25.00 mL of NaOH are added, the number of moles of NaOH and CH₃CO₂H are equal because the amounts of the solutions and their concentrations are the same. All of the CH₃CO₂H has been converted to \(\ce{CH3CO2-}\). The concentration of the \(\ce{CH3CO2-}\) ion is:

\[\mathrm{\dfrac{0.00250\: mol}{0.0500\: L}=0.0500\: \ce{MCH3CO2-}} \nonumber \]

The equilibrium that must be focused on now is the basicity equilibrium for \(\ce{CH3CO2-}\):

\[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(aq)+\ce{OH-}(aq) \nonumber \]

so we must determine K_b for the base by using the ion product constant for water:

\[K_\ce{b}=\ce{\dfrac{[CH3CO2H][OH- ]}{[CH3CO2- ]}} \nonumber \]

\[K_\ce{a}=\ce{\dfrac{[CH3CO2- ][H+]}{[CH3CO2H]}},\textrm{ so }\ce{\dfrac{[CH3CO2H]}{[CH3CO2- ]}}=\dfrac{\ce{[H+]}}{K_\ce{a}}. \nonumber \]

Since K_w = [H⁺][OH⁻]:

\[\begin{align} K_\ce{b} &=\dfrac{\ce{[H+][OH- ]}}{K_\ce{a}} \\ &=\dfrac{K_\ce{w}}{K_\ce{a}} \\ &=\dfrac{1.0\times 10^{-14}}{1.8\times 10^{-5}} \\ &=5.6\times 10^{-10} \end{align} \nonumber \]

Let us denote the concentration of each of the products of this reaction, CH₃CO₂H and OH⁻, as x. Using the assumption that x is small compared to 0.0500 M, \(K_\ce{b}=\dfrac{x^2}{0.0500\:M}\), and then:

\[x=\ce{[OH- ]}=5.3\times 10^{−6} \nonumber \]

\[\ce{pOH}=-\log(5.3\times 10^{-6})=5.28 \nonumber \]

\[\ce{pH}=14.00−5.28=8.72 \nonumber \]

Note that the pH at the equivalence point of this titration is significantly greater than 7.

(c) In (a), 25.00 mL of the NaOH solution was added, and so practically all the CH₃CO₂H was converted into \(\ce{CH3CO2-}\). In this case, only 12.50 mL of the base solution has been introduced, and so only half of all the CH₃CO₂H is converted into \(\ce{CH3CO2-}\). The total initial number of moles of CH₃CO₂H is 0.02500L × 0.100 M = 0.00250 mol, and so after adding the NaOH, the numbers of moles of CH₃CO₂H and \(\ce{CH3CO2-}\) are both approximately equal to \(\mathrm{\dfrac{0.00250\: mol}{2}=0.00125\: mol}\), and their concentrations are the same.

Since the amount of the added base is smaller than the original amount of the acid, the equivalence point has not been reached, the solution remains a buffer, and we can use the Henderson-Hasselbalch equation:

\(\ce{pH}=\ce p K_\ce{a}+\log\ce{\dfrac{[Base]}{[Acid]}}=-\log(\mathit{K}_\ce{a})+\log\ce{\dfrac{[CH3CO2- ]}{[CH3CO2H]}}=-\log(1.8\times 10^{-5})+\log(1)\)

(as the concentrations of \(\ce{CH3CO2-}\) and CH₃CO₂H are the same)

Thus:

\[\ce{pH}=−\log(1.8\times 10^{−5})=4.74 \nonumber \]

(the pH = the pK_a at the halfway point in a titration of a weak acid)

(d) After 37.50 mL of NaOH is added, the amount of NaOH is 0.03750 L × 0.100 M = 0.003750 mol NaOH. Since this is past the equivalence point, the excess hydroxide ions will make the solution basic, and we can again use stoichiometric calculations to determine the pH:

\(\mathrm{[OH^-]=\dfrac{(0.003750\: mol−0.00250\: mol)}{0.06250\: L}}=2.00\times 10^{−2}\:M\)

So:

\(\mathrm{pOH=−\log(2.00\times 10^{−2})=1.70,\: and\: pH=14.00−1.70=12.30}\)

Note that this result is the same as for the strong acid-strong base titration example provided, since the amount of the strong base added moves the solution past the equivalence point.

Exercise \(\PageIndex{2}\)

Calculate the pH for the weak acid/strong base titration between 50.0 mL of 0.100 M HCOOH(aq) (formic acid) and 0.200 M NaOH (titrant) at the listed volumes of added base:

1. 0.00 mL,
2. 15.0 mL,
3. 25.0 mL, and
4. 30.0 mL.

Answer a

0.00 mL: 2.37

Answer b

15.0 mL: 3.92

Answer c

25.00 mL: 8.29

Answer d

30.0 mL: 12.097

Acid-Base Indicators

Certain organic substances change color in dilute solution when the hydronium ion concentration reaches a particular value. For example, phenolphthalein is a colorless substance in any aqueous solution with a hydronium ion concentration greater than 5.0 × 10⁻⁹ M (pH < 8.3). In more basic solutions where the hydronium ion concentration is less than 5.0 × 10⁻⁹ M (pH > 8.3), it is red or pink. Substances such as phenolphthalein, which can be used to determine the pH of a solution, are called acid-base indicators. Acid-base indicators are either weak organic acids or weak organic bases.

The equilibrium in a solution of the acid-base indicator methyl orange, a weak acid, can be represented by an equation in which we use \(\ce{HIn}\) as a simple representation for the complex methyl orange molecule:

\[\underbrace{\ce{HIn (aq)}}_{\ce{red}}+\ce{H2O (l)}⇌\ce{H3O^{+} (aq)}+\underbrace{\ce{In^{-} (aq)}}_{\ce{yellow}} \nonumber \]

\[K_\ce{a}=\ce{\dfrac{[H3O+][In- ]}{[HIn]}}=4.0\times 10^{−4} \nonumber \]

The anion of methyl orange, \(\ce{In^{-}}\), is yellow, and the nonionized form, \(\ce{HIn}\), is red. When we add acid to a solution of methyl orange, the increased hydronium ion concentration shifts the equilibrium toward the nonionized red form, in accordance with Le Chatelier’s principle. If we add base, we shift the equilibrium towards the yellow form. This behavior is completely analogous to the action of buffers.

An indicator’s color is the visible result of the ratio of the concentrations of the two species In⁻ and \(\ce{HIn}\). If most of the indicator (typically about 60−90% or more) is present as \(\ce{In^{-}}\), then we see the color of the \(\ce{In^{-}}\) ion, which would be yellow for methyl orange. If most is present as \(\ce{HIn}\), then we see the color of the \(\ce{HIn}\) molecule: red for methyl orange. For methyl orange, we can rearrange the equation for K_a and write:

\[\mathrm{\dfrac{[In^-]}{[HIn]}=\dfrac{[substance\: with\: yellow\: color]}{[substance\: with\: red\: color]}=\dfrac{\mathit{K}_a}{[H_3O^+]}} \label{ABeq2} \]

Equation \ref{ABeq2} shows us how the ratio of \(\ce{\dfrac{[In- ]}{[HIn]}}\) varies with the concentration of hydronium ion. The above expression describing the indicator equilibrium can be rearranged:

\[ \begin{align} \dfrac{[H_3O^+]}{\mathit{K}_a} &=\dfrac{[HIn]}{[In^- ]} \\[8pt] \log\left(\dfrac{[H_3O^+]}{\mathit{K}_a}\right) &= \log\left(\dfrac{[HIn]}{[In^- ]}\right) \\[8pt] \log([H_3O^+])-\log(\mathit{K}_a) &=-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] -pH+p\mathit{K}_a & =-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] pH &=p\mathit{K}_a+\log\left(\dfrac{[In^-]}{[HIn]}\right) \end {align} \nonumber \]

or in general terms

\[pH=p\mathit{K}_a+\log\left(\dfrac{[base]}{[acid]}\right) \label{HHeq} \]

Equation \ref{HHeq} is the same as the Henderson-Hasselbalch equation, which can be used to describe the equilibrium of indicators.

When [H₃O⁺] has the same numerical value as K_a, the ratio of [In⁻] to [HIn] is equal to 1, meaning that 50% of the indicator is present in the red form (HIn) and 50% is in the yellow ionic form (In⁻), and the solution appears orange in color. When the hydronium ion concentration increases to 8 × 10⁻⁴ M (a pH of 3.1), the solution turns red. No change in color is visible for any further increase in the hydronium ion concentration (decrease in pH). At a hydronium ion concentration of 4 × 10⁻⁵ M (a pH of 4.4), most of the indicator is in the yellow ionic form, and a further decrease in the hydronium ion concentration (increase in pH) does not produce a visible color change. The pH range between 3.1 (red) and 4.4 (yellow) is the color-change interval of methyl orange; the pronounced color change takes place between these pH values.

There are many different acid-base indicators that cover a wide range of pH values and can be used to determine the approximate pH of an unknown solution by a process of elimination. Universal indicators and pH paper contain a mixture of indicators and exhibit different colors at different pHs. Figure \(\PageIndex{2}\) presents several indicators, their colors, and their color-change intervals.

Figure \(\PageIndex{2}\): This chart illustrates the ranges of color change for several acid-base indicators.

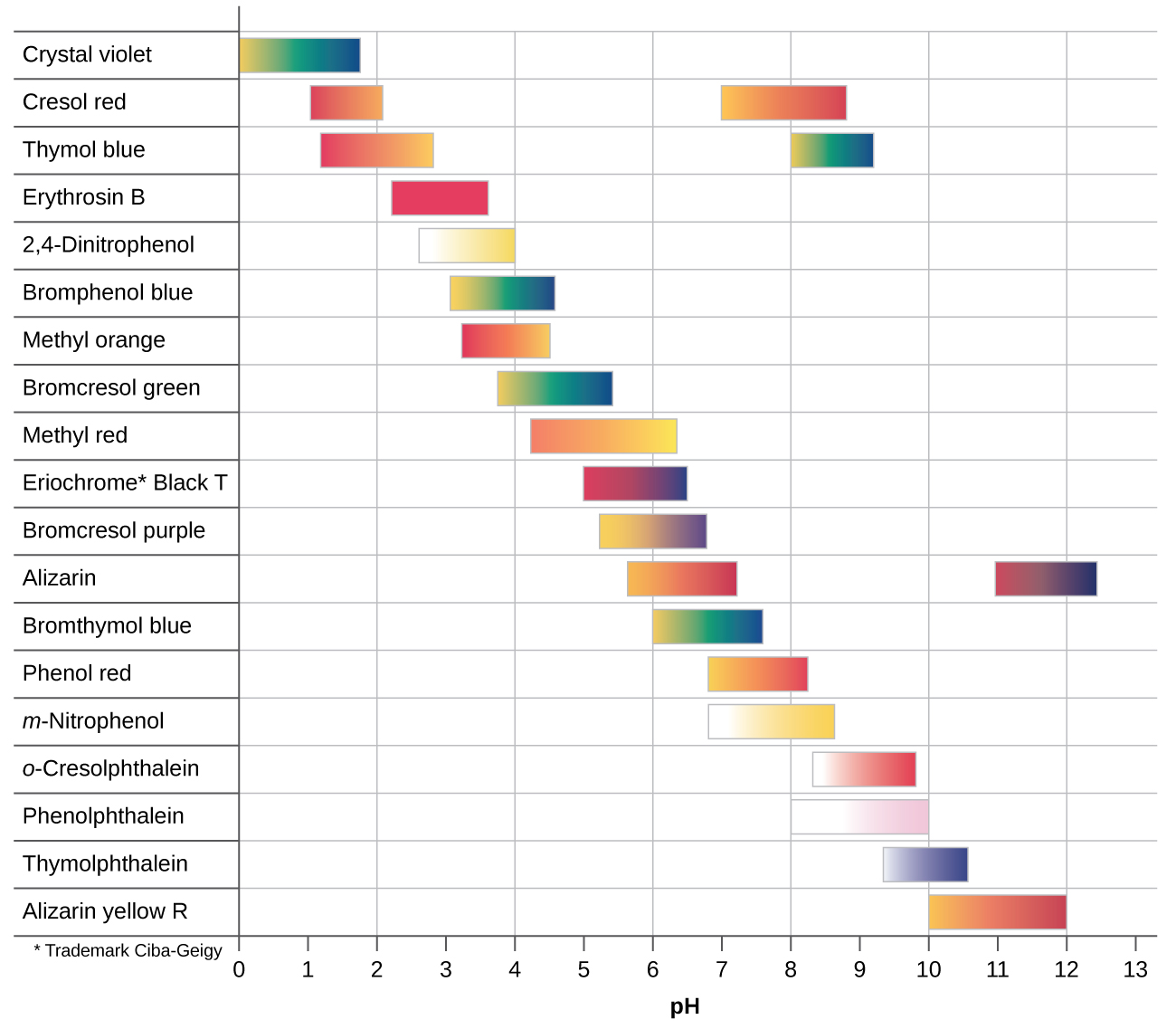
Titration curves help us pick an indicator that will provide a sharp color change at the equivalence point. The best selection would be an indicator that has a color change interval that brackets the pH at the equivalence point of the titration.

The color change intervals of three indicators are shown in Figure \(\PageIndex{3}\). The equivalence points of both the titration of the strong acid and of the weak acid are located in the color-change interval of phenolphthalein. We can use it for titrations of either strong acid with strong base or weak acid with strong base.

Figure \(\PageIndex{3}\): The graph shows a titration curve for the titration of 25.00 mL of 0.100 M CH₃CO₂H (weak acid) with 0.100 M NaOH (strong base) and the titration curve for the titration of HCl (strong acid) with NaOH (strong base). The pH ranges for the color change of phenolphthalein, litmus, and methyl orange are indicated by the shaded areas.

A graph is shown which is titled “Titration of Weak Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L)” and begins at 0 with markings every 5 units up to 50. The vertical axis is labeled “p H” and begins at 0 and increases by single units up to 14. A red curve is drawn on the graph. The curve begins at (0, 3) and passes through the points (5, 4.1), (10, 4.7), (15, 5), (20, 5.5), and (22.5, 6), after which it rapidly increases, forming a vertical section centered at the point (25, 8.7). The rapid increase of the curve then levels off and the curve passes through the points (30, 12), (35, 12.4), (40, 12.5), (45, 12.6), and (50, 12.6). A brown rectangle extends horizontally across the graph covering the p H of 3 to 4.2 range. To the right, this rectangle is labeled “Methyl orange p H range.” A blue rectangle extends horizontally across the graph covering the p H of 4.6 to 8 range. To the right, this rectangle is labeled “Litmus p H range.” A purple rectangle extends horizontally across the graph covering the p H of 8.4 to 10 range. To the right, this rectangle is labeled “Phenolphthalein p H range.” The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 8.72.”

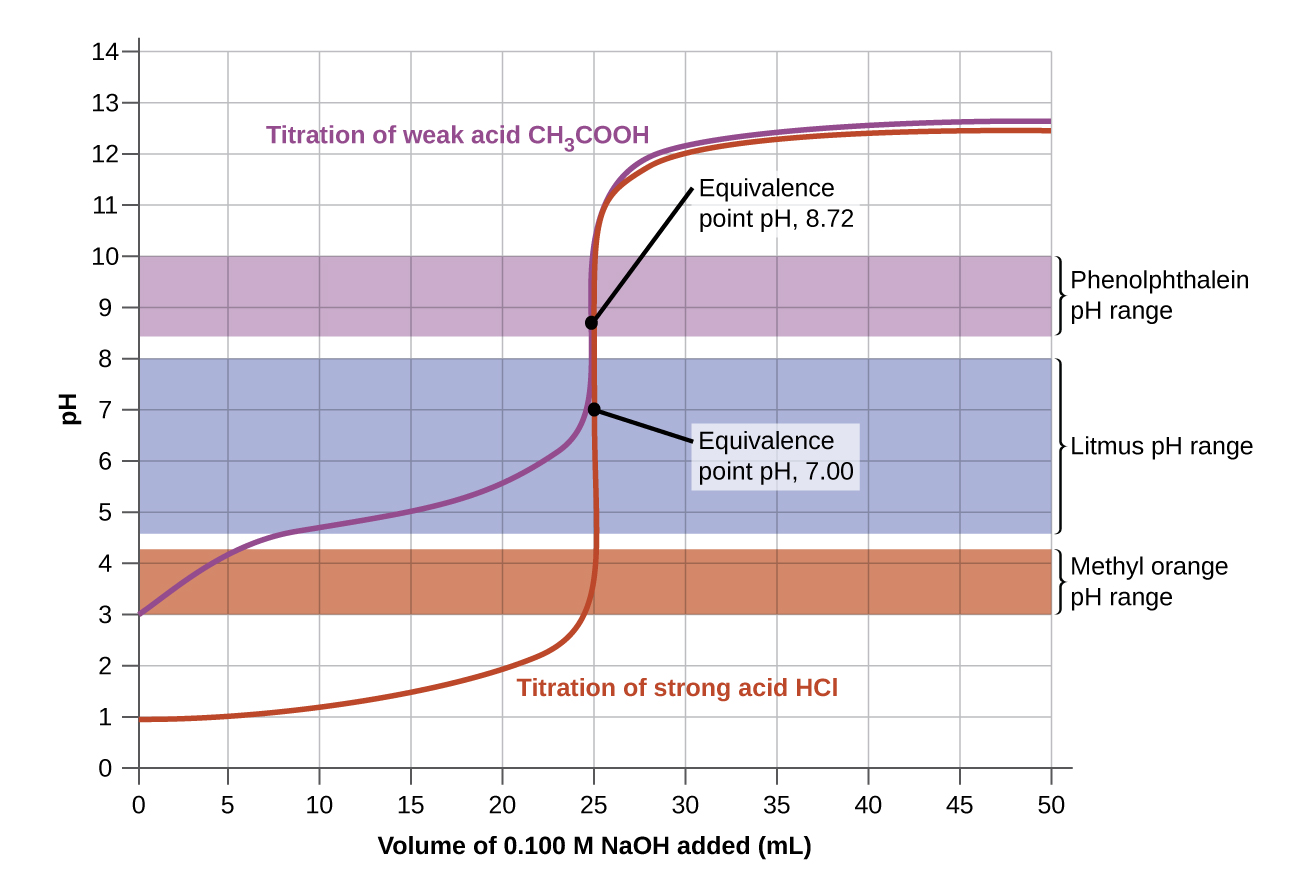
Litmus is a suitable indicator for the HCl titration because its color change brackets the equivalence point. However, we should not use litmus for the CH₃CO₂H titration because the pH is within the color-change interval of litmus when only about 12 mL of NaOH has been added, and it does not leave the range until 25 mL has been added. The color change would be very gradual, taking place during the addition of 13 mL of NaOH, making litmus useless as an indicator of the equivalence point.

We could use methyl orange for the HCl titration, but it would not give very accurate results: (1) It completes its color change slightly before the equivalence point is reached (but very close to it, so this is not too serious); (2) it changes color, as Figure \(\PageIndex{2}\) demonstrates, during the addition of nearly 0.5 mL of NaOH, which is not so sharp a color change as that of litmus or phenolphthalein; and (3) it goes from yellow to orange to red, making detection of a precise endpoint much more challenging than the colorless to pink change of phenolphthalein. Figure \(\PageIndex{2}\) shows us that methyl orange would be completely useless as an indicator for the CH₃CO₂H titration. Its color change begins after about 1 mL of NaOH has been added and ends when about 8 mL has been added. The color change is completed long before the equivalence point (which occurs when 25.0 mL of NaOH has been added) is reached and hence provides no indication of the equivalence point.

We base our choice of indicator on a calculated pH, the pH at the equivalence point. At the equivalence point, equimolar amounts of acid and base have been mixed, and the calculation becomes that of the pH of a solution of the salt resulting from the titration.

Summary

A titration curve is a graph that relates the change in pH of an acidic or basic solution to the volume of added titrant. The characteristics of the titration curve are dependent on the specific solutions being titrated. The pH of the solution at the equivalence point may be greater than, equal to, or less than 7.00. The choice of an indicator for a given titration depends on the expected pH at the equivalence point of the titration, and the range of the color change of the indicator.

Glossary

acid-base indicator

organic acid or base whose color changes depending on the pH of the solution it is in

color-change interval

range in pH over which the color change of an indicator takes place

titration curve

plot of the pH of a solution of acid or base versus the volume of base or acid added during a titration