15.6: Free Energy and Equilibrium
- Page ID
- 78940
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)You are expected to be able to define and explain the significance of terms identified in italic type.
- As a homogeneous chemical reaction proceeds, the Gibbs energies of the reactants become more negative and those of the products more positive as the composition of the system changes.
- The total Gibbs energy of the system (reactants + products) always becomes more negative as the reaction proceeds. Eventually it reaches a minimum value at a system composition that defines the equilibrium composition of the system, after which time no further net change will occur.
- The equilibrium constant for the reaction is determined the standard Gibbs energy change:
ΔG° = -RT ln Kp - The sign of the temperature dependence of the equilibrium constant is governed by the sign of ΔH°. This is the basis of the Le Chatelier Principle.
- The Gibbs energies of solid and liquid components are constants that do not change with composition. Thus in heterogeneous reactions such as phase changes, the total Gibbs energy does not pass through a minimum and when the system is not at equilibrium only all-products or all-reactants will be stable.
- Two reactions are coupled when the product of one reaction is consumed in the other. If ΔG° for the first reaction is positive, the overall process can still be spontaneous if ΔG° for the second reaction is sufficiently negative— in which case the second reaction is said to "drive" the first reaction.
Under conditions of constant temperature and pressure, chemical change will tend to occur in whatever direction leads to a decrease in the value of the Gibbs energy. In this lesson we will see how G varies with the composition of the system as reactants change into products. When G falls as far as it can, all net change comes to a stop. The equilibrium composition of the mixture is determined by ΔG° which also defines the equilibrium constant K.
The Road to Equilibrium is Down the Gibbs Energy Hill
This means, of course, that if the total Gibbs energy \(G\) of a mixture of reactants and products goes through a minimum value as the composition changes, then all net change will cease— the reaction system will be in a state of chemical equilibrium. You will recall that the relative concentrations of reactants and products in the equilibrium state is expressed by the equilibrium constant. In this lesson we will examine the relation between the Gibbs energy change for a reaction and the equilibrium constant.
To keep things as simple as possible, we will consider a homogeneous chemical reaction of the form
\[A + B \rightleftharpoons C + D\]
in which all components are gases at the temperature of interest. If the sum of the standard Gibbs energies of the products is less than that of the reactants, ΔG° for the reaction will be negative and the reaction will proceed to the right. But how far? If the reactants are completely transformed into products, the equilibrium constant would be infinity. The equilibrium constants we actually observe all have finite values, implying that even if the products have a lower Gibbs energy than the reactants, some of the latter will always remain when the process comes to equilibrium.
A homogeneous reaction is one in which everything takes place in a single gas or liquid phase.
To understand how equilibrium constants relate to ΔG° values, assume that all of the reactants are gases, so that the Gibbs energy of gas A, for example, is given at all times by
\[G_A = G_A^° + RT \ln P_A \label{5-1}\]
The Gibbs energy change for the reaction is sum of the Gibbs energies of the products, minus the sum of Gibbs energies of the reactants:
\[\Delta G = \underbrace{G_C + G_D}_{\text{products}} \underbrace{– G_A – G_B}_{\text{reactants}} \label{5-2}\]
Using Equation \(\ref{5-1}\) to expand each term on the right of Equation \ref{5-2}, we have
\[\Delta G = (G^°_C + RT \ln P_C) + (G^°_D + RT \ln P_D) – (G^°_B + RT \ln P_B) – (G^°_A + RT \ln P+A) \label{5-3}\]
We can now express the \(G^°\) terms collectively as \(\Delta G^°\), and combine the logarithmic pressure terms into a single fraction
\[ \Delta G = \Delta G° + RT \ln \left( \dfrac{P_CP_D}{P_AP_B} \right) \label{5-4}\]
which is more conveniently expressed in terms of the reaction quotient \(Q\).
\[\Delta{G} = \Delta G^° + RT \ln Q \label{5-5}\]
The Gibbs energy \(G\) is a quantity that becomes more negative during the course of any natural process. Thus as a chemical reaction takes place, \(G\) only falls and will never become more positive. Eventually a point is reached where any further transformation of reactants into products would cause \(G\) to increase. At this point \(G\) is at a minimum (see below), and no further net change can take place; the reaction is then at equilibrium.
Although Equations \ref{5-1}-\ref{5-5} are strictly correct only for perfect gases, we will see later that equations of similar form can be applied to many liquid solutions by substituting concentrations for pressures.
Consider the gas-phase dissociation reaction
\[\ce{N_2O_4 \rightarrow 2 NO_2 } \nonumber\]
which is a simple example of the Gibbs energy relationships in a homogeneous reaction.
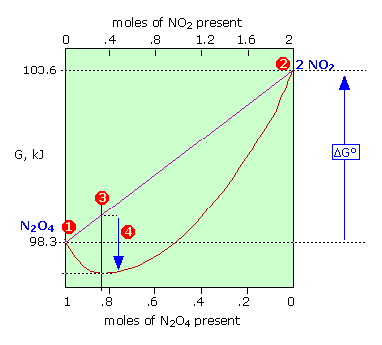
The Gibbs energy of 1 mole of N2O4 (1) is smaller than that of 2 moles of NO2 (2) by 5.3 kJ; thus \( \Delta G^o = +5.3\, \text{kJ}\) for the complete transformation of reactants into products. The straight diagonal line shows the Gibbs energy of all possible compositions if the two gases were prevented from mixing. The red curved line show the Gibbs energy of the actual reaction mixture. This passes through a minimum at (3) where 0.814 mol of \(N_2O_4\) are in equilibrium with 0.372 mol of \(NO_2\). The difference (4) corresponds to the Gibbs energy of mixing of reactants and products which always results in an equilibrium mixture whose Gibbs energy is lower than that of either pure reactants or pure products. Thus some amount of reaction will occur even if ΔG° for the process is positive.
What’s the difference between ΔG and ΔG°?
It’s very important to be aware of this distinction; that little ° symbol makes a world of difference! First, the standard Gibbs energy change ΔG° has a single value for a particular reaction at a given temperature and pressure; this is the difference
\[ \sum G^°_{f} (\text{products}) – \sum G^°_{f}(\text{reactants}) \]
that are tabulated in thermodynamic tables. It corresponds to the Gibbs energy change for a process that never really happens: the complete transformation of pure N2O4 into pure NO2 at a constant pressure of 1 atm.
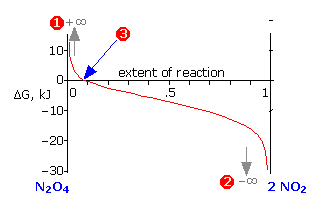
The other quantity \(\Delta G\), defined by Equation \(\ref{5-5}\), represents the total Gibbs energies of all substances in the reaction mixture at any particular system composition. In contrast to \(\Delta G^°\) which is a constant for a given reaction, \(\Delta G\) varies continuously as the composition changes, finally reaching zero at equilibrium. \(\Delta G\) is the “distance” (in Gibbs energy) from the equilibrium state of a given reaction. Thus for the limiting cases of pure \(\ce{N_2O_4}\) or \(\ce{NO_2}\) (as far from the equilibrium state as the system can be!),
\[Q = \dfrac{[NO_2]^2}{[N_2O_4]} = \pm\infty\]
which makes the logarithm in Equation \(\ref{5-5}\), and thus the value of \(\Delta G\), approach the same asymptotic limits (1) or (2). As the reaction proceeds in the appropriate direction \(\Delta G\) approaches zero; once there (3), the system is at its equilibrium composition and no further net change will occur.
The standard molar Gibbs energy change for this very simple reaction is –2.26 kJ, but mixing of the unreacted butane with the product brings the Gibbs energy of the equilibrium mixture down to about –3.1 kJ mol–1 at the equilibrium composition corresponding to 77 percent conversion.
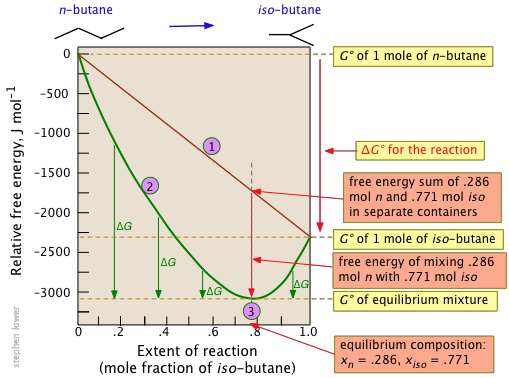
Notice particularly that
- The sum of the Gibbs energies of the two gases (n-butane and iso-butane) separately varies linearly with the composition of the mixture (red line
 ).
). - The green curve
 adds the Gibbs energy of mixing to the above sum; its minimum defines the equilibrium composition.
adds the Gibbs energy of mixing to the above sum; its minimum defines the equilibrium composition. - As the composition approaches the equilibrium value
 , \(ΔG\) (which denotes how much farther the Gibbs energy of the system can fall) approaches zero.
, \(ΔG\) (which denotes how much farther the Gibbs energy of the system can fall) approaches zero.
The detailed calculations that lead to the values shown above can be found here.
Why reactions lead to mixtures of reactants and products
We are now in a position to answer the question posed earlier: if ΔG° for a reaction is negative, meaning that the Gibbs energies of the products are more negative than those of the reactants, why will some of the latter remain after equilibrium is reached? The answer is that no matter how low the Gibbs energy of the products, the Gibbs energy of the system can be reduced even more by allowing some of the products to be "contaminated" (i.e., diluted) by some reactants. Owing to the entropy associated with mixing of reactants and products, no homogeneous reaction will be 100% complete. An interesting corollary of this is that any reaction for which a balanced chemical equation can be written can in principle take place to some extent, however minute that might be.
Gibbs energies of mixing of products with reactants tend to be rather small, so for reactions having ΔG° values that are highly negative or positive (±20 kJ mol–1, say), the equilibrium mixture will, for all practical purposes, be either [almost] "pure" reactants or products.
The Equilibrium Constant
Now let us return to Equation \(\ref{5-5}\) which we reproduce here:
\[\Delta{G} = \Delta{G^°} + RT \ln Q \]
As the reaction approaches equilibrium, \(\Delta G\) becomes less negative and finally reaches zero. At equilibrium \(\Delta{G} = 0\) and \(Q = K\), so we can write (must know this!)
\[\Delta{G^°} = –RT \ln K_p \label{5-6}\]
in which \(K_p\), the equilibrium constant expressed in pressure units, is the special value of \(Q\) that corresponds to the equilibrium composition.
This equation is one of the most important in chemistry because it relates the equilibrium composition of a chemical reaction system to measurable physical properties of the reactants and products. If you know the entropies and the enthalpies of formation of a set of substances, you can predict the equilibrium constant of any reaction involving these substances without the need to know anything about the mechanism of the reaction.
Instead of writing Equation \(\ref{5-6}\) in terms of Kp, we can use any of the other forms of the equilibrium constant such as Kc (concentrations), Kx (mole fractions), Kn(numbers of moles), etc. Remember, however, that for ionic solutions especially, only the Ka, in which activities are used, will be strictly valid.
It is often useful to solve Equation \(\ref{5-6}\) for the equilibrium constant, yielding
\[ K = \exp {\left ( {-\Delta G \over RT} \right )} \label{5-7}\]

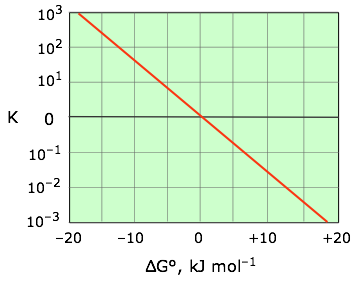
This relation is most conveniently plotted against the logarithm of \(K\) as shown in Figure \(\PageIndex{3}\), where it can be represented as a straight line that passes through the point (0,0).
Calculate the equilibrium constant for the reaction from the following thermodynamic data:
\[\ce{H^{+}(aq) + OH^{–}(aq) <=> H_2O(l)} \nonumber\]
|
\(H^+(aq)\) |
|---|
* Note that the standard entropy of the hydrogen ion is zero by definition. This reflects the fact that it is impossible to carry out thermodynamic studies on a single charged species. All ionic entropies are relative to that of \(\ce{H^{+}(aq)}\), which explains why some values (as for aqueous hydroxide ion) are negative.
Solution
From the above data, we can evaluate the following quantities:
\[\begin{align*} \Delta{H}^o &= \sum \Delta H^o_{f}(\text{products}) - \sum \Delta H^o_{f}(\text{reactants}) \\[4pt] &= (–285.8) - (-230) \\[4pt] &= –55.8\, kJ \; mol^{-1} \end{align*}\]
\[\begin{align*}\Delta{S}^o &= \sum \Delta S^o (\text{products}) - \sum \Delta S° (\text{reactants}) \\[4pt] &= (70.0) – (–10.9) \\[4pt] &= +80.8\, J \; K^{-1}\; mol^{-1} \end{align*}\]
The value of \(\Delta{G}°\) at 298 K is
\[\begin{align*} \Delta H^o – T\Delta S^o &= (–55800) – (298)(80.8) \\[4pt] &= –79900\, J\, mol^{–1} \end{align*}\]
From Equation \(\ref{5-7}\) we have
\[\begin{align*} K &= \exp\left(\dfrac{–79900}{8.314 \times 298}\right) \\[4pt] &= e^{32.2} = 1.01 \times 10^{–14} \end{align*}\]
Equilibrium and Temperature
We have already discussed how changing the temperature will increase or decrease the tendency for a process to take place, depending on the sign of ΔS°. This relation can be developed formally by differentiating the relation
\[ \Delta G^° = \Delta H^° – T\Delta S^° \label{5-8}\]
with respect to the temperature:
\[ \dfrac{d(-\Delta G^°)}{dT} = -\Delta S^° \label{5-9}\]
Hence, the sign of the entropy change determines whether the reaction becomes more or less allowed as the temperature increases.
We often want to know how a change in the temperature will affect the value of an equilibrium constant whose value is known at some fixed temperature. Suppose that the equilibrium constant has the value \(K_1\) at temperature \(T_1\) and we wish to estimate \(K_2\) at temperature \(T_2\). Expanding Equation \(\ref{5-7}\) in terms of \(\Delta H^°\) and \(\Delta S^°\), we obtain
\[–RT_1 \ln K_1 = \Delta H^ ° – T_1 \Delta S^° \]
and
\[–RT_2 \ln K_2 = \Delta H ^° – T_2 \Delta S^°\]
Dividing both sides by RT and subtracting, we obtain
\[ \ln K_1 - \ln K_2 = - \left( \dfrac{\Delta H^°}{RT_1} -\dfrac{\Delta H^°}{RT_2} \right) \label{5-10}\]
Which is most conveniently expressed as the ratio
\[ \ln \dfrac{K_1}{K_2} = - \dfrac{\Delta H^°}{R} \left( \dfrac{1}{T_1} -\dfrac{1}{T_2} \right) \label{5-11}\]
This is its theoretical foundation of Le Chatelier's Principle with respect to the effect of the temperature on equilibrium:
- if the reaction is exothermic \(\Delta H^° < 0\), then increasing temperature will make the second exponential term smaller and \(K\) will decrease. The equilibrium will then “shift to the left”.
- If \(\Delta H^° > 0\), then increasing T will make the exponent less negative and \(K\) will increase and the equilibrium will “shift to the right”.
This is an extremely important relationship, but not just because of its use in calculating the temperature dependence of an equilibrium constant. Even more important is its application in the “reverse” direction to experimentally determine ΔH° from two values of the equilibrium constant measured at different temperatures. Direct calorimetric determinations of heats of reaction are not easy to make; relatively few chemists have the equipment and experience required for this rather exacting task. Measurement of an equilibrium constant is generally much easier, and often well within the capabilities of anyone who has had an introductory Chemistry course. Once the value of ΔH° is determined it can be combined with the Gibbs energy change (from a single observation of K, through Equation \(\ref{5-7}\)) to allow ΔS° to be calculated through Equation \(\ref{5-9}\).
Equilibrium Without Mixing: it's all or nothing
You should now understand that for homogeneous reactions (those that take place entirely in the gas phase or in solution) the equilibrium composition will never be 100% products, no matter how much lower their Gibbs energy relative to the reactants. As was summarized in the N2O4-dissociation example discussed previously. This is due to "dilution" of the products by the reactants. In heterogeneous reactions (those which involve more than one phase) this dilution, and the effects that flow from it, may not be possible.
A particularly simple but important type of a heterogeneous process is phase change. Consider, for example, an equilibrium mixture of ice and liquid water. The concentration of H2O in each phase is dependent only on the density of the phase; there is no way that ice can be “diluted” with water, or vice versa. This means that at all temperatures other than the freezing point, the lowest Gibbs energy state will be that corresponding to pure ice or pure liquid. Only at the freezing point, where the Gibbs energies of water and ice are identical, can both phases coexist, and they may do so in any proportion.

Gibbs energy of the ice-water system
Only at 0°C can ice and liquid water coexist in any proportion. Note that in contrast to the homogeneous N2O4 example, there is no Gibbs energy minimum at intermediate compositions.
Coupled Reactions
Two reactions are said to be coupled when the product of one of them is the reactant in the other:
\[A \rightarrow B \nonumber\]
and
\[B \rightarrow C \nonumber\]
If the standard Gibbs energy of the first reaction is positive but that of the second reaction is sufficiently negative, then for the overall process will be negative and we say that the first reaction is “driven” by the second one. This, of course, is just another way of describing an effect that you already know as the Le Chatelier principle: the removal of substance B by the second reaction causes the equilibrium of the first to “shift to the right”. Similarly, the equilibrium constant of the overall reaction is the product of the equilibrium constants of the two steps.
| 1 Cu2S(s) → 2 Cu(s) + S(s) | ΔG° = + 86.2 kJ | ΔH° = + 76.3 kJ |
| 2 S(s) + O2(g)→ SO2(g) | ΔG° = –300.1 kJ | ΔH° = + 296.8 kJ |
| 3 Cu2S(s)→ 2 Cu(s) + SO2(g) | ΔG° = –213.9 kJ | ΔH° = – 217.3 kJ |
In the above example, reaction 1 is the first step in obtaining metallic copper from one of its principal ores. This reaction is endothermic and it has a positive Gibbs energy change, so it will not proceed spontaneously at any temperature. If Cu2S is heated in the air, however, the sulfur is removed as rapidly as it is formed by oxidation in the highly spontaneous reaction 2, which supplies the Gibbs energy required to drive 1. The combined process, known as roasting, is of considerable industrial importance and is one of a large class of processes employed for winning metals from their ores.


