9.4: Polar Covalence

Learning Objectives

Make sure you thoroughly understand the following essential ideas which have been presented below.

• Define electronegativity, and describe the general way in which electronegativities depend on the location of an element in the periodic table.
• Explain how electronegativity values relate to the polar nature of a chemical bond.
• What two factors determine the magnitude of an electric dipole moment ?
• Sketch structural diagrams that illustrate how the presence of polar bonds in a molecule can either increase or diminish the magnitude of the molecular dipole moment.
• Calculate the formal charge of each atom in a structure, and comment on its significance in relation to the polarity of that structure.
• Select the more likely of two or more electron-dot structures for a given species.
• Explain the difference between formal charge and oxidation number.
• Describe the limiting cases of covalent and ionic bonds. Explain what both categories of bonds have in common.

The electrons constituting a chemical bond are simultaneously attracted by the electrostatic fields of the nuclei of the two bonded atoms. In a homonuclear molecule such as O₂ the bonding electrons will be shared equally by the two atoms. In general, however, differences in the sizes and nuclear charges of the atoms will cause one of them to exert a greater attraction on the bonding pair, causing the electron cloud to be displaced toward the more strongly-attracting atom.

Electronegativity

The electronegativity of an atom denotes its relative electron-attracting power in a chemical bond. It is important to understand that electronegativity is not a measurable property of an atom in the sense that ionization energies and electron affinities are, although it can be correlated with both of these properties. The actual electron-attracting power of an atom depends in part on its chemical environment (that is, on what other atoms are bonded to it), so tabulated electronegativities should be regarded as no more than predictors of the behavior of electrons, especially in more complicated molecules. There are several ways of computing electronegativities, which are expressed on an arbitrary scale. The concept of electronegativity was introduced by Linus Pauling and his 0-4 scale continues to be the one most widely used.

The 0-4 electronegativity scale of Pauling is the best known of several arbitrary scales of this kind. Electronegativity values are not directly observable, but are derived from measurable atomic properties properties such as ionization energy and electron affinity. The place of any atom on this scale provides a good indication of its ability to compete with another atom in attracting a shared electron pair to it, but the presence of bonds to other atoms, and of multiple- or nonbonding electron pairs may make predictions about the nature a given bond less reliable.

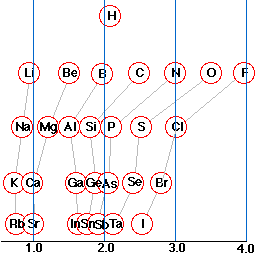
An atom that has a small electronegativity is said to be electropositive. As the diagram shows, the metallic elements are generally electropositive. The position of hydrogen in this regard is worth noting; although physically a nonmetal, much of its chemistry is metal-like.

Dipole moments

When non-identical atoms are joined in a covalent bond, the electron pair will be attracted more strongly to the atom that has the higher electronegativity. As a consequence, the electrons will not be shared equally; the center of the negative charges in the molecule will be displaced from the center of positive charge. Such bonds are said to be polar and to possess partial ionic character, and they may confer a polar nature on the molecule as a whole.

A polar molecule acts as an electric dipole which can interact with electric fields that are created artificially or that arise from nearby ions or polar molecules. Dipoles are conventionally represented as arrows pointing in the direction of the negative end. The magnitude of interaction with the electric field is given by the permanent electric dipole moment of the molecule. The dipole moment corresponding to an individual bond (or to a diatomic molecule) is given by the product of the quantity of charge displaced q and the bond length r:

\[μ = q \times r\]

In SI units, q is expressed in coulombs and r in meters, so μ has the dimensions of \(C \cdot m\). If one entire electron charge is displaced by 100 pm (a typical bond length), then

\[μ = (1.6022 \times 10^{–19}\; C) \times (10^{–10}\; m) = 1.6 \times 10^{–29}\; C \cdot m = 4.8 \;D\]

The quantity denoted by D, the Debye unit, is still commonly used to express dipole moments. It was named after Peter Debye (1884-1966), the Dutch-American physicist who pioneered the study of dipole moments and of electrical interactions between particles; he won the Nobel Prize for Chemistry in 1936.

How dipole moments are measured

When a solution of polar molecules is placed between two oppositely-charged plates, they will tend to align themselves along the direction of the field. This process consumes energy which is returned to the electrical circuit when the field is switched off, an effect known as electrical capacitance.

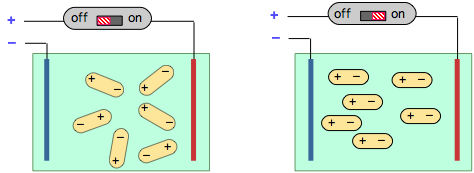
Measurement of the capacitance of a gas or solution is easy to carry out and serves as a means of determining the magnitude of the dipole moment of a substance.

Example \(\PageIndex{1}\)

Estimate the percent ionic character of the bond in the hydrogen fluoride molecule from the experimental data shown at the right.

Solution

Dipole moments as vector sums

In molecules containing more than one polar bond, the molecular dipole moment is just the vector combination of what can be regarded as individual "bond dipole moments". Being vectors, these can reinforce or cancel each other, depending on the geometry of the molecule; it is therefore not uncommon for molecules containing polar bonds to be nonpolar overall, as in the example of carbon dioxide:

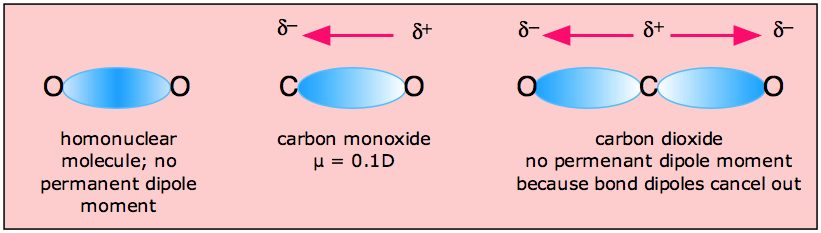
The zero dipole moment of CO₂ is one of the simplest experimental methods of demonstrating the linear shape of this molecule.

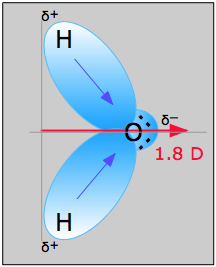
H₂O, by contrast, has a very large dipole moment which results from the two polar H–O components oriented at an angle of 104.5°. The nonbonding pairs on oxygen are a contributing factor to the high polarity of the water molecule. In molecules containing nonbonding electrons or multiple bonds, the elecronegativity difference may not correctly predict the bond polarity. A good example of this is carbon monoxide, in which the partial negative charge resides on the carbon, as predicted by its negative formal charge (below.)

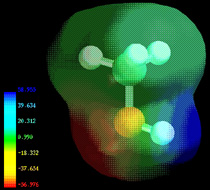
Electron densities in a molecule (and the dipole moments that unbalanced electron distributions can produce) are now easily calculated by molecular modeling programs. In this example, for methanol CH₃OH, the blue area centered on hydrogen represents a positive charge, the red area centered where we expect the lone pairs to be located represents a negative charge, while the light green around methyl is approximately neutral. The manner in which the individual bonds contribute to the dipole moment of the molecule is nicely illustrated by the series of chloromethanes:

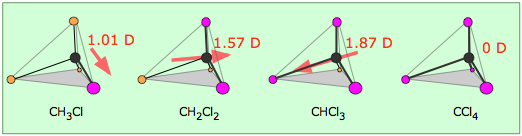
(Bear in mind that all four positions around the carbon atom are equivalent in this tetrahedral molecule, so there are only four chloromethanes.)

Formal charge and oxidation number

Although the total number of valence electrons in a molecule is easily calculated, there is not always a simple and unambiguous way of determining how many reside in a particular bond or as non-bonding pairs on a particular atom. For example, one can write valid Lewis octet structures for carbon monoxide showing either a double or triple bond between the two atoms, depending on how many nonbonding pairs are placed on each: C::O::: and :C:::O: (see Problem Example 3 below). The choice between structures such as these is usually easy to make on the principle that the more electronegative atom tends to surround itself with the greater number of electrons. In cases where the distinction between competing structures is not all that clear, an arbitrarily-calculated quantity known as the formal charge can often serve as a guide.

The formal charge on an atom is the electric charge it would have if all bonding electrons were shared equally with its bonded neighbors.

The formal charge on an atom is calculated by the following formula:

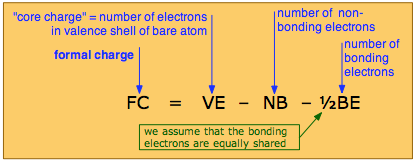
in which the core charge is the electric charge the atom would have if all its valence electrons were removed. In simple cases, the formal charge can be worked out visually directly from the Lewis structure, as is illustrated farther on.

Example \(\PageIndex{2}\): Formal Charge

Find the formal charges of all the atoms in the sulfuric acid structure shown here.

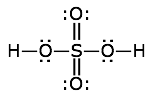
Solution

The atoms here are hydrogen, sulfur, and double- and single-bonded oxygens. Remember that a double bond is made up of two electron-pairs.

• hydrogen: FC = 1 – 0 – 1 = 0
• sulfur: FC = 6 – 0 – 6 = 0
• hydroxyl oxygen: FC = 6 – 4 – 2 = 0
• double-bonded oxygen: FC = 6 – 4 – 2 = 0

Using formal charge to select the best Lewis structure

The general rule for choosing between alternative structures is that the one involving the smallest formal charges is most favored, although the following example shows that this is not always the case.

Example \(\PageIndex{1}\): Carbon Monoxide

Write out some structures for carbon monoxide CO, both those that do and do not obey the octet rule, and select the "best" on the basis of the formal charges.

Solution

Structure that obeys the octet rule:

a) For :C:::O: Carbon: 4 – 2 – 3 = –1; Oxygen: 6 – 2 – 3 = +1

Structures that do not obey the octet rule (for carbon):

b) For :C:O::: Carbon: 4 – 2 – 1 = +1; Oxygen: 6 – 6 – 1 = –1

c) For :C::O:: Carbon: 4 – 2 –2 = 0; Oxygen: 6 – 4 – 2 = 0

Comment: All three structures are acceptable (because the formal charges add up to zero for this neutral molecule) and contribute to the overall structure of carbon monoxide, although not equally. Both experiment and more advanced models show that the triple-bonded form (a) predominates. Formal charge, which is no more than a bookkeeping scheme for electrons, is by itself unable to predict this fact.

In a species such as the thiocyanate ion \(SCN^-\) in which two structures having the same minimal formal charges can be written, we would expect the one in which the negative charge is on the more electronegative atom to predominate.

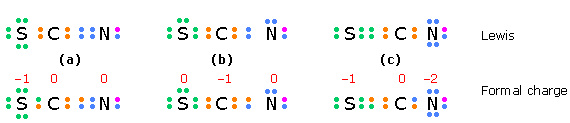
The electrons in the structures of the top row are the valence electrons for each atom; an additional electron (purple) completes the nitrogen octet in this negative ion. The electrons in the bottom row are divided equally between the bonded atoms; the difference between these numbers and those above gives the formal charges.

Formal charge can also help answer the question “where is the charge located?” that is frequently asked about polyatomic ions. Thus by writing out the Lewis structure for the ammonium ion NH₄⁺, you should be able to convince yourself that the nitrogen atom has a formal charge of +1 and each of the hydrogens has 0, so we can say that the positive charge is localized on the central atom.

Oxidation number

This is another arbitrary way of characterizing atoms in molecules. In contrast to formal charge, in which the electrons in a bond are assumed to be shared equally, oxidation number is the electric charge an atom would have if the bonding electrons were assigned exclusively to the more electronegative atom. Oxidation number serves mainly as a tool for keeping track of electrons in reactions in which they are exchanged between reactants, and for characterizing the “combining power” of an atom in a molecule or ion.

The following diagram compares the way electrons are assigned to atoms in calculating formal charge and oxidation number in carbon monoxide.

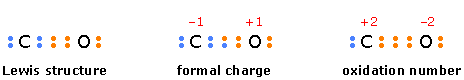
Ionic compounds

The shared-electron pair model introduced by G.N. Lewis showed how chemical bonds could form in the absence of electrostatic attraction between oppositely-charged ions. As such, it has become the most popular and generally useful model of bonding in all substances other than metals. A chemical bond occurs when electrons are simultaneously attracted to two nuclei, thus acting to bind them together in an energetically-stable arrangement. The covalent bond is formed when two atoms are able to share a pair of electrons:

In general, however, different kinds of atoms exert different degrees of attraction on their electrons, so in most cases the sharing will not be equal. One can even imagine an extreme case in which the sharing is so unequal that the resulting "molecule" is simply a pair of ions:

The resulting substance is sometimes said to contain an ionic bond. Indeed, the properties of a number of compounds can be adequately explained using the ionic model. But does this mean that there are really two kinds of chemical bonds, ionic and covalent? According to the ionic electrostatic model, solids such as NaCl consist of positive and negative ions arranged in a crystal lattice. Each ion is attracted to neighboring ions of opposite charge, and is repelled by ions of like charge; this combination of attractions and repulsions, acting in all directions, causes the ion to be tightly fixed in its own location in the crystal lattice.

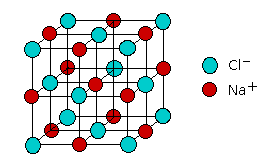
Since electrostatic forces are nondirectional, the structure of an ionic solid is determined purely by geometry: two kinds of ions, each with its own radius, will fall into whatever repeating pattern will achieve the lowest possible potential energy. Surprisingly, there are only a small number of possible structures; one of the most common of these, the simple cubic lattice of NaCl, is shown here.

Is there such as thing as an ionic bond?

When two elements form an ionic compound, is an electron really lost by one atom and transferred to the other one? In order to deal with this question, consider the data on the ionic solid LiF. The average radius of the neutral Li atom is about 2.52Å. Now if this Li atom reacts with an atom of F to form LiF, what is the average distance between the Li nucleus and the electron it has “lost” to the fluorine atom? The answer is 1.56Å; the electron is now closer to the lithium nucleus than it was in neutral lithium!

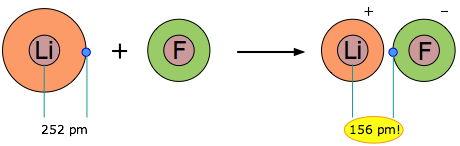
So the answer to the above question is both yes and no: yes, the electron that was now in the 2s orbital of Li is now within the grasp of a fluorine 2p orbital, but no, the electron is now even closer to the Li nucleus than before, so how can it be “lost”? The one thing that is inarguably true about LiF is that there are more electrons closer to positive nuclei than there are in the separated Li and F atoms. But this is just the rule we stated at the beginning of this unit: chemical bonds form when electrons can be simultaneously near two or more nuclei.

It is obvious that the electron-pair bond brings about this situation, and this is the reason for the stability of the covalent bond. What is not so obvious (until you look at the numbers such as are quoted for LiF above) is that the “ionic” bond results in the same condition; even in the most highly ionic compounds, both electrons are close to both nuclei, and the resulting mutual attractions bind the nuclei together. This being the case, is there really any fundamental difference between the ionic and covalent bond?

The answer, according to modern chemical thinking is probably “no”; in fact, there is some question as to whether it is realistic to consider that these solids consist of “ions” in the usual sense. The preferred picture that seems to be emerging is one in which the electron orbitals of adjacent atom pairs are simply skewed so as to place more electron density around the “negative” element than around the “positive” one.

This being said, it must be reiterated that the ionic model of bonding is a useful one for many purposes, and there is nothing wrong with using the term “ionic bond” to describe the interactions between the atoms in the very small class of “ionic solids” such as LiF and NaCl.

"Covalent, ionic or metallic" is an oversimplification!

If there is no such thing as a “completely ionic” bond, can we have one that is completely covalent? The answer is yes, if the two nuclei have equal electron attracting powers. This situation is guaranteed to be the case with homonuclear diatomic molecules-- molecules consisting of two identical atoms. Thus in Cl₂, O₂, and H₂, electron sharing between the two identical atoms must be exactly even; in such molecules, the center of positive charge corresponds exactly to the center of negative charge: halfway between the two nuclei.

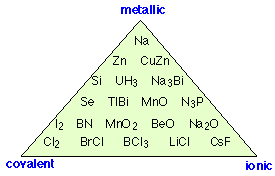
Categorizing all chemical bonds as either ionic, covalent, or metallic is a gross oversimplification; as this diagram shows, there are examples of substances that exhibit varying degrees of all three bonding characteristics.

Dative (Coordinate) covalent Bonds

In most covalent bonds, we think of the electron pair as having a dual parentage, one electron being contributed by each atom. There are, however, many cases in which both electrons come from only one atom. This can happen if the donor atom has a non-bonding pair of electrons and the acceptor atom has a completely empty orbital that can accommodate them. These are called dative or coordinate covalent bonds.

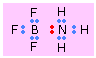
This is the case, for example, with boron trifluoride and ammonia. In BF₃, one the 2p orbitals is unoccupied and can accommodate the lone pair on the nitrogen atom of ammonia. The electron acceptor, BF₃, acts as a Lewis acid here, and NH₃ is the Lewis base. Bonds of this type (sometimes known as coordinate covalent or dative bonds) tend to be rather weak (usually 50-200kJ/mol); in many cases the two joined units retain sufficient individuality to justify writing the formula as a molecular complex or adduct.