9.3: Models of Chemical Bonding
- Page ID
- 3514
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential ideas which have been presented.
- Comment on the distinction between a theory and a model in the context of chemical bonding.
- What is meant by a classical model of chemical bonding?
Why do atoms bind together— sometimes? The answer to this question would ideally be a simple, easily understood theory that would not only explain why atoms bind together to form molecules, but would also predict the three-dimensional structures of the resulting compounds as well as the energies and other properties of the bonds themselves. Unfortunately, no one theory exists that accomplishes these goals in a satisfactory way for all of the many categories of compounds that are known. Moreover, it seems likely that if such a theory does ever come into being, it will be far from simple.
About Models in Science
When we are faced the need to find a scientific explanation for a complex phenomenon such as bonding, experience has shown that it is often best to begin by developing a model. A scientific model is something like a theory in that it should be able to explain observations and to make useful predictions. But whereas a theory can be discredited by a single contradictory case, a model can be useful even if it does not encompass all instances of the effects it attempts to explain. We do not even require that a model be a credible representation of reality; all we ask is that it be able to explain the behavior of those cases to which it is applicable in terms that are consistent with the model itself.
An example of a model that you may already know about is the kinetic molecular theory of gases. Despite its name, this is really a model (at least at the level that beginning students use it) because it does not even try to explain the observed behavior of real gases. Nevertheless, it serves as a tool for developing our understanding of gases, and as an essential starting point for more elaborate treatments.
One thing is clear: chemical bonding is basically electrical in nature, the result of attraction between bodies of opposite charge; bonding occurs when outer-shell electrons are simultaneously attracted to the positively-charged nuclei of two or more nearby atoms. The need for models arises when we try to understand why
- Not all pairs of atoms can form stable bonds
- Different elements can form different numbers of bonds (this is expressed as "combining power" or "valence".)
- The geometric arrangement of the bonds ("bonding geometry") around a given kind of atom is a property of the element.
Given the extraordinary variety of ways in which atoms combine into aggregates, it should come as no surprise that a number of useful bonding models have been developed. Most of them apply only to certain classes of compounds or attempt to explain only a restricted range of phenomena. In this section we will provide brief descriptions of some of the bonding models; the more important of these will be treated in much more detail in later lessons in this unit.
Some early views of chemical bonding
Intense speculation about “chemical affinity” began in the 18th century. Some likened the tendency of one atom to “close” with another as an expression of a human-like kind of affection. Others attributed bonding to magnetic-like forces (left) or to varying numbers of “hooks” on different kinds of atoms (right). The latter constituted a primitive (and extremely limited) way of explaining the different combining powers (valances) of the different elements.
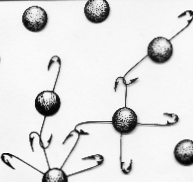
"There are no such things..."
Napoleon's definition of history as a set of lies agreed on by historians seems to have a parallel with chemical bonding and chemists. At least in Chemistry, we can call the various explanations "models" and get away with it even if they are demonstrably wrong, as long as we find them useful. In a provocative article (J Chem Educ 1990 67(4) 280-298), J. F. Ogilvie tells us that there are no such things as orbitals, or, for that matter, non-bonding electrons, bonds, or even uniquely identifiable atoms within molecules. This idea disturbed a lot of people (teachers and textbook authors preferred to ignore it) and prompted a spirited rejoinder (J Chem Ed 1992 69(6) 519-521) from Linus Pauling, father of the modern quantum-mechanical view of the chemical bond.
But the idea has never quite gone away. Richard Bader of McMaster University has developed a quantitative "atoms in molecules" model that depicts molecules as a collection of point-like nuclei embedded in a diffuse cloud of electrons. There are no "bonds" in this model, but only "bond paths" that correspond to higher values of electron density along certain directions that are governed by the manner in which the positive nuclei generate localized distortions of the electron cloud.
Classical models of the chemical bond
By classical, we mean models that do not take into account the quantum behavior of small particles, notably the electron. These models generally assume that electrons and ions behave as point charges which attract and repel according to the laws of electrostatics. Although this completely ignores what has been learned about the nature of the electron since the development of quantum theory in the 1920’s, these classical models have not only proven extremely useful, but the major ones also serve as the basis for the chemist’s general classification of compounds into “covalent” and “ionic” categories.
The Ionic Model
Ever since the discovery early in the 19th century that solutions of salts and other electrolytes conduct electric current, there has been general agreement that the forces that hold atoms together must be electrical in nature. Electrolytic solutions contain ions having opposite electrical charges; opposite charges attract, so perhaps the substances from which these ions come consist of positive and negatively charged atoms held together by electrostatic attraction.
It turns out that this is not true generally, but a model built on this assumption does a fairly good job of explaining a rather small but important class of compounds that are called ionic solids. The most well known example of such a compound is sodium chloride, which consists of two interpenetrating lattices of Na+ and Cl– ions arranged in such as way that every ion of one type is surrounded (in three dimensional space) by six ions of opposite charge.
One can envision the formation of a solid NaCl unit by a sequence of events in which one mole of gaseous Na atoms lose electrons to one mole of Cl atoms, followed by condensation of the resulting ions into a crystal lattice:
| Na(g) → Na+(g) + e– | +494 kJ | ionization energy |
|---|---|---|
| Cl(g) + e– → Cl–(g) | –368 kJ | electron affinity |
| Na+(g) + Cl–(g) | –498 kJ | lattice energy |
| Na(g) + Cl(g) → NaCl(s) | –372 kJ | Sum: Na-Cl bond energy |
Note: positive energy values denote endothermic processes, while negative ones are exothermic.
Since the first two energies are known experimentally, as is the energy of the sum of the three processes, the lattice energy can be found by difference. It can also be calculated by averaging the electrostatic forces exerted on each ion over the various directions in the solid, and this calculation is generally in good agreement with observation, thus lending credence to the model. The sum of the three energy terms is clearly negative, and corresponds to the liberation of heat in the net reaction (bottom row of the table), which defines the Na–Cl “bond” energy.
The ionic solid is more stable than the equivalent number of gaseous atoms simply because the three-dimensional NaCl structure allows more electrons to be closer to more nuclei. This is the criterion for the stability of any kind of molecule; all that is special about the “ionic” bond is that we can employ a conceptually simple electrostatic model to predict the bond strength.
The main limitation of this model is that it applies really well only to the small class of solids composed of Group 1 and 2 elements with highly electronegative elements such as the halogens. Although compounds such as CuCl2 dissociate into ions when they dissolve in water, the fundamental units making up the solid are more like polymeric chains of covalently-bound CuCl2 molecules that have little ionic character.
Shared-electron (covalent) model
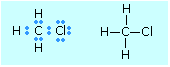 This model originated with the theory developed by G.N. Lewis in 1916, and it remains the most widely-used model of chemical bonding. It is founded on the idea that a pair of electrons shared between two atoms can create a mutual attraction, and thus a chemical bond.
This model originated with the theory developed by G.N. Lewis in 1916, and it remains the most widely-used model of chemical bonding. It is founded on the idea that a pair of electrons shared between two atoms can create a mutual attraction, and thus a chemical bond.
Usually each atom contributes one electron (one of its valence electrons) to the pair, but in some cases both electrons come from one of the atoms. For example, the bond between hydrogen and chlorine in the hydrogen chloride molecule is made up of the single 1s electron of hydrogen paired up with one of chlorine's seven valence (3p) electrons. The stability afforded by this sharing is thought to derive from the noble gas configurations (helium for hydrogen, argon for chlorine) that surround the bound atoms.
The origin of the electrostatic binding forces in this model can best be understood by examining the simplest possible molecule. This is the hydrogen molecule ion H2+, which consists of two nuclei and one electron.
First, however, think what would happen if we tried to make the even simpler molecule H22+. Since this would consist only of two protons whose electrostatic charges would repel each other at all distances, it is clear that such a molecule cannot exist; something more than two nuclei are required for bonding to occur.
H2+ we have a third particle, the electron. The effect of this electron will depend on its location with respect to the two nuclei. If the electron is in the space between the two nuclei (the binding region in the diagram), it will attract both protons toward itself, and thus toward each other. If the total attraction energy exceeds the internuclear repulsion, there will be a net bonding effect and the molecule will be stable. If, on the other hand, the electron is off to one side (in an antibinding region), it will attract both nuclei, but it will attract the closer one much more strongly, owing to the inverse-square nature of Coulomb’s law. As a consequence, the electron will now actively work ag against bonding by helping to push the two nuclei apart.Polar covalent model
A purely covalent bond can only be guaranteed when the electronegativities (electron-attracting powers) of the two atoms are identical. When atoms having different electronegativities are joined, the electrons shared between them will be displaced toward the more electronegative atom, conferring a polarity on the bond which can be described in terms of percent ionic character.
Coulombic model
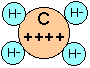 This is an extension of the ionic model to compounds that are ordinarily considered to be non-ionic. Combined hydrogen is always considered to exist as the hydride ion H–, so that methane can be treated as if it were C4+ H–4.
This is an extension of the ionic model to compounds that are ordinarily considered to be non-ionic. Combined hydrogen is always considered to exist as the hydride ion H–, so that methane can be treated as if it were C4+ H–4.
This is not as bizarre as it might seem at first if you recall that the proton has almost no significant size, so that it is essentially embedded in an electron pair when it is joined to another atom in a covalent bond. This model, which is not as well known as it deserves to be, has surprisingly good predictive power, both as to bond energies and structures.
VSEPR model
The “valence shell electron repulsion” model is not so much a model of chemical bonding as a scheme for explaining the shapes of molecules. It is based on the quantum mechanical view that bonds represent electron clouds— physical regions of negative electric charge that repel each other and thus try to stay as far apart as possible. We will explore this concept in much greater detail in a later unit.
3 Quantum-mechanical models
These models of bonding take into account the fact that a particle as light as the electron cannot really be said to be in any single location. The best we can do is define a region of space in which the probability of finding the electron has some arbitrary value which will always be less than unity. The shape of this volume of space is called an orbital and is defined by a mathematical function that relates the probability to the (x,y,z) coordinates of the molecule.
Like other models of bonding, the quantum models attempt to show how more electrons can be simultaneously close to more nuclei. Instead of doing so through purely geometrical arguments, they attempt this by predicting the nature of the orbitals which the valence electrons occupy in joined atoms.
The hybrid orbital model
This was developed by Linus Pauling in 1931 and was the first quantum-based model of bonding. It is based on the premise that if the atomic s,p, and d orbitals occupied by the valence electrons of adjacent atoms are combined in a suitable way, the hybrid orbitals that result will have the character and directional properties that are consistent with the bonding pattern in the molecule. The rules for bringing about these combinations turn out to be remarkably simple, so once they were worked out it became possible to use this model to predict the bonding behavior in a wide variety of molecules. The hybrid orbital model is most usefully applied to the p-block elements in the first few rows of the periodic table, and is especially important in organic chemistry.
The molecular orbital model
This model takes a more fundamental approach by regarding a molecule as a collection of valence electrons and positive cores. Just as the nature of atomic orbitals derives from the spherical symmetry of the atom, so will the properties of these new molecular orbitals be controlled by the interaction of the valence electrons with the multiple positive centers of these atomic cores.
These new orbitals, unlike those of the hybrid model, are delocalized; that is, they do not “belong” to any one atom but extend over the entire region of space that encompasses the bonded atoms. The available (valence) electrons then fill these orbitals from the lowest to the highest, very much as in the Aufbau principle that you learned for working out atomic electron configurations. For small molecules (which are the only ones we will consider here), there are simple rules that govern the way that atomic orbitals transform themselves into molecular orbitals as the separate atoms are brought together. The real power of molecular orbital theory, however, comes from its mathematical formulation which lends itself to detailed predictions of bond energies and other properties.
The electron-tunneling model
A common theme uniting all of the models we have discussed is that bonding depends on the fall in potential energy that occurs when opposite charges are brought together. In the case of covalent bonds, the shared electron pair acts as a kind of “electron glue” between the joined nuclei. In 1962, however, it was shown that this assumption is not strictly correct, and that instead of being concentrated in the space between the nuclei, the electron orbitals become even more concentrated around the bonded nuclei. At the same time however, they are free to “move” between the two nuclei by a process known as tunneling.
This refers to a well-known quantum mechanical effect that allows electrons (or other particles small enough to exhibit wavelike properties) to pass (“tunnel”) through a barrier separating two closely adjacent regions of low potential energy. One result of this is that the effective volume of space available to the electron is increased, and according to the uncertainty principle this will reduce the kinetic energy of the electron.
According to this model, the bonding electrons act as a kind of fluid that concentrates in the region of each nucleus (lowering the potential energy) and at the same time is able to freely flow between them (reducing the kinetic energy). Despite its conceptual simplicity and full acknowledgment of the laws of quantum mechanics, this model is less known than it deserves to be and is unfortunately absent from most textbooks.


