Chapter 10: Appendix- Spectroscopy
- Page ID
- 354130
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
How we know what we know about the structure of matter? If you think back to our discussions of atomic structure, one of the most important pieces of evidence for the nature of atoms – particularly the arrangement of their electrons – was the way the atoms interact with electromagnetic radiation, that is, light. For example: the idea that both the energy of electromagnetic radiation and that of electrons is quantized came from Einstein’s analysis of the photoelectric effect. Electrons are ejected from metals only if they interact with photons of sufficient and discrete amounts of energy. More evidence for quantized electron energy states was provided from the study of atomic absorption and emission spectra, as photons of energy corresponding to the energy gaps between electron energy levels are either absorbed or emitted by electrons. Photons with the “wrong” amount of energy are not absorbed. Now that we have studied different assemblies of atoms (molecules, ions, networked structures), we can also look at how these larger entities interact with energy (in the form of electromagnetic radiation).
Interactions of electromagnetic radiation and electrons in molecules: As we have seen, just as electrons occupy atomic orbitals in atoms, the electrons in molecules occupy molecular orbitals. As with atomic orbitals, electrons in molecular orbitals can absorb or release photons of a specific energy as they move from one molecular orbital to another. However, there is a significant difference between the absorption/emission process in isolated atoms (or ions) and that of molecules. When an electron is promoted to a higher energy level in an atom, the product is an atom in an excited state – generally the excited atom (or ion) will decay back to the ground state by emitting a photon. \(\mathrm{A} + hν \rightarrow \mathrm{A}^{*} (\text{excited state}) \rightarrow \mathrm{A} (\text{ground state}) + hν\)

However, when an electron within a molecule is excited it moves (or is “promoted”) from its original molecular orbital to another. Now there are a number of different consequences that may occur. For example, if the electron absorbs a photon and is promoted from a bonding molecular orbital to an anti-bonding orbital, the result will be that the bond will break, since there is now no overall stabilizing interaction. Consider \(\mathrm{H–H}\), which is the simplest possible molecule. The set of molecular orbitals for hydrogen includes a σ bonding and a \(\sigma^{*}\) anti-bonding orbital. In the ground (or lowest energy) state, molecular hydrogen has a σ bonding orbital containing both of the molecule’s electrons. If one of the bonding electrons absorbs a photon that has just the right amount of energy (the energy difference between the bonding and anti-bonding orbital) it will be promoted and move into the destabilized anti-bonding orbital – causing the bond between the atoms to break. As you might imagine, if chemical bonds were susceptible to breaking merely by being exposed to low energy electromagnetic radiation, such as that of visible light, the world would be a different (and rather boring) place. For example, life would not be possible, since it depends upon the stability of molecules.
The energy of the photons required to bring about bond breaking is quite large. For example, the energy required to break an \(\mathrm{H–H}\) bond (the bond energy) is \(436 \mathrm{~kJ/mol}\). If you calculate the wavelength of a photon that could deliver this amount of energy, the amount of energy required to break one \(\mathrm{H–H}\) bond would be in the far UV section of the electrogmagnetic spectrum (\(\sim 280\mathrm{nm}\)). The typically strong covalent sigma (or single) bond requires quite high energy photons to break them.
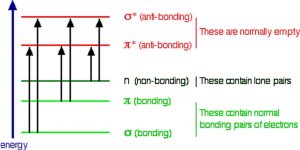
So the question is, if the Earth’s atmosphere blocks out most (\(>98 \%\)) of high energy (ultraviolet) photons and most biologically important molecules cannot absorb visible light, why is there a need for sunscreen, which filters out the UV A (\(400-315 \mathrm{~nm}\)) and UV B (\(315-280 \mathrm{~nm}\)) photons. The answer is that a most biological molecules contain more than simple σ bonds. For example, most complex biological molecules also contain π bonds and non-bonding electrons in addition to \(\sigma\) bonds; transitions between these orbitals may be observed as these orbitals require less energy to be effected. As you can see in the figure, the energy gaps between these orbitals are quite different and are smaller than the \(\sigma - \sigma^{*}\) difference. Photons with enough energy to cause these electron transitions are present in sunlight. For example, a double bond has both a \(\sigma\) and a \(\pi\) bond. Absorption of a photon that would promote an electron from a pi bonding orbital to a \(\pi^{*}\) anti-bonding orbital would have the effect of breaking the original \(\pi\) bond. One way to represent this is shown here \(\rightarrow\). One of electrons that was in the \(\pi\) bond is now in the high energy \(\pi^{*}\) antibonding orbital and is far more reactive.
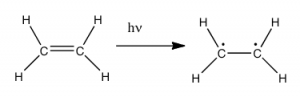
Another way to think about it is that the electrons are now unpaired, and are much more likely to react to form a more stable entity.[1] An obvious way to regain stability is for the electron in the \(\pi\) antibonding orbital to drop back down to the bonding energy level and emit a photon of the same energy, and in most cases this is what happens – ultimately causing no damage. One caveat here is that since double bonds are rotationally constrained, it is possible that rotation can occur around the single (\(\sigma\)) bond before the π bond reforms; this leads to an isomer of the original alkene. On the other hand, if there is a nearby potentially reactive species, reactions between molecules (or in the case of biological macromolecules, between distinct regions of these molecules) can occur. For example, most of us are aware that exposure to the sun causes skin damage that can lead to skin cancer. A major mechanism for these effects involves \(\mathrm{DNA}\). Where two thymidine bases are adjacent to one another, a UV photon can be absorbed by a π bond in one thymine base. This broken π bond (and resulting unpaired electron) is very reactive. It can react with a π bond in an adjacent thymine-moeity leading to a new bond, a reaction that produces a four membered carbon ring, known as a thymine dimer. The \(\mathrm{DNA}\) replication machinery cannot accurately replicate a sequence containing a thymine dimer, resulting in a change in \(\mathrm{DNA}\) sequence – a mutation. Mutations of this type are a common early step in the generation of a cancerous skin cells.[2]

A more benign example of photon absorption in biological systems underlies the mechanism by which we (and other organisms) detect light, that is how we can see things! While it was originally thought (at least by some) that vision involved rays emitted from eyes,[3] we now understand that to see we need to detect photons that are reflected or emitted by the objects around us. The process begins when the photons of light fall on cells known as photoreceptors. In our eyes, these cells are located within the retina, a sheet of cells than line the interior surface of the eye. Within a subset of retinal cells are a number of different types of molecules that contain π bonds. These molecules are proteins known generically as opsins. An opsin is composed of a polypeptide (or apoprotein) that is covalently bound to another molecule, 11-cis-retinal.[4] This molecule is derived from vitamin A (all trans retinol). The complex of apoprotein and retinal is the functional opsin protein. There are a number of different opsin components that influence the wavelength of the photons absorbed by the functional opsin protein. When a photon is absorbed, it promotes an electron from one of the retinal’s π bonds (between \(C_{11}\) and \(C_{12}\)) to an antibonding orbital. Instead of reacting with another molecule, like thymine, there is a rotation around the remaining single (\(\sigma\)) bond, and then the re-formation of the \(\pi\) bond, which leads to the isomerization of the original 11-cis form into the trans isomer. This change in the shape of the retinal moiety in turn influences the shape of the opsin protein which initiates a cascade of electrochemical events that carry signals to the rest of the brain (the retina is considered an extension of the brain) that are eventually recognized as visual input.

UV-Vis spectroscopy and chromophores – or why are carrots orange? One common recommendation from doctors is that we eat plenty of highly colored fruits and vegetables. The compounds that give these foods their strong color have a number of commonalities. For example, the compound that gives carrots and sweet potatoes their distinctive orange color is beta-carotene. You might well notice its similarity to retinal. The compound that contributes to the red color of tomatoes is lycopene. Molecules of this type are known generically as pigments.

The wavelengths at which a compound absorbs light depends on the energy gap between the orbitals that are involved in the transition. This energy gap is determined by the structure of the molecule. A molecule with only single bonds absorbs light at shorter wavelengths (in the high energy UV), while more complex bonding patterns are associated with the absorption of visible light. For example, the presence of multiple π bonds and their interactions within the molecule can affect the energy gap between the molecular orbitals. Recall our discussion of graphite. Rather than thinking of graphite as sheets of fused six membered rings with alternating single and double bonds, we can think of each bond as a localized σ bond and a delocalized π bond. There are huge numbers of \(\pi\) molecular orbitals spread over the whole sheet of carbon atoms. The more \(\pi\) MO’s there are the more the energy gap between these orbital decreases, that is, the less energy (longer wavelength light) is needed to move an electron from a \(\pi\) to \(\pi^{*}\) orbital. In the case of network substances like graphite and metals, the energy gap between the orbitals becomes negligible, and we think of the bonding model as a band of molecular orbitals. In these cases, many wavelengths of light can be absorbed and then re-emitted which gives graphite and metals their characteristic shininess. In substances like lycopene or \(\beta\)-carotene we also find this pattern of alternating single and double bonds. We say that compounds with this pattern of alternating single and double bonds (e.g. \(\mathrm{–C=C–C=C–}\)) are conjugated, and we can model the bonding in the same way as graphite. There are \(\pi\) MO’s that can extend over the region of the molecule, and the more orbitals there are, the closer together in energy they get.
For an isolated \(\mathrm{C=C}\) double bond, the energy required to promote an electron from the \(\pi\) to the \(\pi^{*}\) orbital corresponds to the light in the UV region (around \(170 \mathrm{~nm}\)), but as the number of double bonds that are conjugated (separated by single bonds) increases, the energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) decreases. Eventually, the wavelength of light needed to promote an electron from the HOMO to the LUMO moves into the visible region, and the substance becomes colored. (Note that it does not become the color of the light that is absorbed – but rather the remaining light that is transmitted or reflected). These conjugated regions of molecules are called chromophores.[5] The longer the conjugated section of the molecule, the longer the wavelength that is absorbed. You will notice that both lycopene and B-carotene contain large chromophore regions.
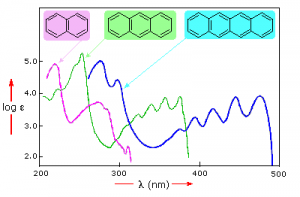
Samples of UV-VIS absorption spectra are shown here. Note that in contrast to the atomic absorption spectra we saw earlier which consisted of sharp lines corresponding to the wavelength of light absorbed by atoms, these spectra are broad and ill defined. In addition, you can see that the longer (larger) the chromophore the longer the wavelength that is absorbed, and each of these compounds appears to be a different color.
The fact that the peaks in these spectra are not sharp means that UV-VIS spectroscopy is typically not used for identification of compounds (see below for IR and NMR spectroscopy which can be used for this purpose). However the amount of light absorbed is proportional to the concentration of the substance and therefore UV-VIS spectroscopy can be used to determine the concentration of samples. There are other optical behaviors associated with complex molecules in organisms, including molecular systems that that emit light, a process known as bioluminescence that we will not discuss here.[6]
InfraRed spectroscopy – looking at molecular vibrations: Up to now we have concentrated on the absorption (and emission) of energy caused by transitions of electrons between quantized energy levels. However, as we discussed earlier, electron energies are not the only quantized energies at the atomic-molecular level. In molecules, the energies of both molecular vibrations and rotations are also quantized, but the energies involved are much lower than those needed to break bonds. When two atoms are bonded, the atoms can move back and forth relative to each other: as they move, the potential energy of the two atom system changes (why is that?). There are also motions associated with rotations around bonds. But (weirdly, and quantum mechanically) rather than being able to assume any value, the energies of these vibrations (and rotations) are also quantized. The energy gaps between the vibrational energy levels tend to be in the range of infrared radiation. When we look at the light absorbed or emitted by vibrational energy changes we are doing what is known as infrared spectroscopy. Transitions from one rotational energy level to anther can be promoted by microwave radiation, leading to microwave spectroscopy. The table below provides examples of different types of spectroscopy, the wavelength of electromagnetic radiation typically involved, and the uses of each kind of spectroscopy.
| Type of Spectroscopy | Radiation wavelength | Interaction with matter | Purpose |
|---|---|---|---|
| UV-VIS | \(350-700 \mathrm{~nm}\) | Electronic transitions in molecules | Often used to determine concentrations |
| IR | \(2,500-16,000 \mathrm{~nm}\) | Molecular vibrations | To determine presence of particular groups of atoms (functional groups |
| NMR | \(10-100 \mathrm{~m}\) | Nuclear transitions | Identify types of C and H in molecules |
| MRI | \(10-100 \mathrm{~m}\) | Nuclear transitions | Imaging (typically human body parts) |
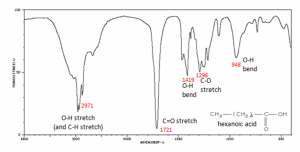
Why, you might ask, are we interested in the vibrations and rotations of molecules? It turns out that many molecules and fragments of molecules have very distinctive IR absorption patterns that can be used to identify them. The figure shows an IR spectrum of a carboxylic acid and how the various peaks can be ascribed to vibrations of different bonds or groups within the molecule. Infrared spectroscopy allows us to identify substances from these patterns, both in the lab and for example in interstellar dust clouds. The presence of quite complex molecules in space (hundreds of millions of light years away from earth) has been detected by the use of IR spectroscopy.

Nuclear Magnetic Resonance Spectroscopy (NMR): NMR is a form of spectroscopy which uses the fact that certain nuclei can, depending on their structure, behave like tiny spinning magnets. Two of the most common nuclei used for NMR spectroscopy are \({}^{1}\mathrm{H}\) and \({}^{13}\mathrm{C}\). When materials that contain carbon or hydrogen atoms in them are placed in a magnetic field, there are two possible orientations of these nuclei can exist in with respect to the field: a low energy orientation in which the nuclear magnet is aligned with the field, and a high energy orientation in which the nuclear magnet is aligned against the field. The effect of this is to split the energy levels of the nuclei. This makes it possible to cause a transition between the two energy levels by the absorption of electromagnetic radiation of appropriate energy- which in this instance, is in the radio wave range.
The exact energy of these changes depends upon the environment of the nuclei, if the \(\mathrm{C}\) or \(\mathrm{H}\) is in an electron deficient environment it will appear at a different frequency in the spectrum than a \(\mathrm{C}\) or \(\mathrm{H}\) that is surrounded by more electron density (the nucleus is said to be shielded by the electrons.) From a study of the different energies absorbed as the nucleus flips from one spin state to another, it is possible derive information about the structure of the compound.
The information that can be ained from simple NMR spectra has to do with the number and type of nuclei that are in a certain compound. The simplest type of NMR spectrum is based on \({}^{13}\mathrm{C}\). \({}^{13}\mathrm{C}\) is a minor isotope of carbon (about 1% of natural abundance) and is present in all naturally occurring samples of carbon compounds. In a \({}^{13}\mathrm{C}\) spectrum, each carbon atom in the molecule will give rise to a signal or peak in the spectrum based on its chemical environment. For example, ethanol (\(\mathrm{CH}_{3}\mathrm{CH}_{2}\mathrm{OH}\)) has two peaks in its \({}^{13}\mathrm{C}\) spectrum because there are two, and only two distinct chemical environments that a carbon atom can “inhabit”. In contrast, cyclohexenone produces a spectrum that has six distinct peaks, because each of the six carbon atoms in the molecule inhabits a distinctly different environment. Benzene (\(\mathrm{C}_{6}\mathrm{H}_{6}\)) on the other hand has only one signal in its \({}^{13}\mathrm{C}\) NMR spectrum since there is only one type of carbon in this molecule, all the positions in the ring are equivalent. (Draw out the Lewis structure to convince yourself that this is true)



Proton or \({}^{1}\mathrm{H}\) NMR spectra appear more complicated because each hydrogen atom tends to give a signal that is split into several different peaks. This is because each \(\mathrm{H}\) nucleus can be affected by the neighboring nuclei. This produces multiple energy levels for each \(\mathrm{H}\), which results in more complex spectra. \({}^{13}\mathrm{C}\) appears simpler because there are typically only one (or zero) \({}^{13}\mathrm{C}\) nucleus in any molecule, therefore there are no interactions by nearby carbons (\({}^{12}\mathrm{C}\) does not have different nuclear energy levels in a magnetic field). Note that this \({}^{1}\mathrm{H}\) NMR spectrum is much more complex than the \({}^{13}\mathrm{C}\) NMR. However, there are five distinct clusters of signals and there are five kinds of protons in the compound that gives rise to this spectrum
A variant of NMR is Magnetic Resonance Imaging (MRI), which is based on the same underlying nuclear behaviors, but uses a somewhat different approach. In MRI the material (usually a person) from which you want to record the spectrum is placed in a large magnet which separates the nuclear spin states as described above. The target is irradiated with a pulse of radiowaves that promotes all the nuclei up to their highest accessible energy state. As the nuclei decay back to the lower spin state they emit photons. Instead of detecting the energies of these photons, the system records the times it takes for photons to be emitted as the nuclei drop back to their lowest energy states. These times are dependent on the environment of the nuclei making it possible, through data manipulation, to develop internal visualizations of the body in the scanner.
These are just a few types of examples of spectroscopy. There are many more that you may encounter, but typically these methods all depend on recording how matter and energy interact and using that data to determine the arrangement of the atoms in the matter that is under investigation.
Thumbnail: White light is dispersed by a prism into the colors of the visible spectrum. (CC BY-SA 3.0; D-Kuru).


