6.E: Chemical Kinetics (Exercises)

Reaction Rates

Exercise \(\PageIndex{1}\)*

What is the difference between average rate, initial rate, and instantaneous rate?

Answer

The reaction rate is the measure of the change in concentration of the reactants or products per unit time.

Average rate: The change in concentration of a reactant (or product) divided by a specific time interval

Instantaneous rate: The reaction rate at a specific given moment during the reaction.

Initial rate: The instantaneous rate at the start of the reaction (when the product begins to form).

Exercise \(\PageIndex{2}\)*

Ozone decomposes to oxygen according to the equation \(\ce{2O3}(g)⟶\ce{3O2}(g)\). Write the equation that relates the rate expressions for this reaction in terms of the disappearance of O₃ and the formation of O₂.

Answer

For the general reaction \(aA \rightarrow bB\), the rate can be expressed in terms of the disappearance of (A) or the appearance of (B) as follows:

\[-\dfrac{1}{a}\dfrac{\Delta [A]}{\Delta t} = \dfrac{1}{b}\dfrac{\Delta [B]}{\Delta t} \nonumber\]

 

The rate of a reaction is defined to be positive. Since the concentration of a reactant, [A], decreases, we use a negative sign to ensure the rate remains positive.

The rate must be normalized according to the stoichiometry of the reaction. In the decomposition of ozone to oxygen, two moles of ozone form three moles of oxygen gas. Therefore, the rate of the reaction can be described as:

\[ \text{Rate} = -\frac{\Delta [\ce{O3}]}{2\Delta t} = \frac{\Delta [\ce{O2}]}{3\Delta t} \nonumber\]

Exercise \(\PageIndex{3}\)*

In the nuclear industry, chlorine trifluoride is used to prepare uranium hexafluoride, a volatile compound of uranium used in the separation of uranium isotopes. Chlorine trifluoride is prepared by the reaction \(\ce{Cl2}(g)+\ce{3F2}(g)⟶\ce{2ClF3}(g)\). When [Cl₂] is decreasing at 0.10 M/s, how fast is [ClF₃] increasing?

Answer

\[rate=-\frac{{\Delta}[Cl_2]}{{\Delta}t}=\frac {1}{2}\frac{{\Delta}[ClF_3]}{{\Delta}t}\nonumber \]

\[\frac{{\Delta}[ClF_3]}{{\Delta}t}=0.20 M/s\nonumber \]

Exercise \(\PageIndex{4}\)*

Consider the following reaction in aqueous solution:

\[\ce{5Br-}(aq)+\ce{BrO3-}(aq)+\ce{6H+}(aq)⟶\ce{3Br2}(aq)+\ce{3H2O}(l)\nonumber \]

If the rate of disappearance of Br^–(aq) at a particular moment during the reaction is 3.5 × 10⁻⁴ M s⁻¹, what is the rate of appearance of Br₂(aq) at that moment?

Answer

Step 1. Define the rate of the reaction.

Recall:

For the general reaction: aA + bB → cC+ dD

\(rate =- \frac{\Delta[A]}{a\Delta{t}}=- \frac{\Delta[B]}{b\Delta{t}}= \frac{\Delta[C]}{c\Delta{t}}=\frac{\Delta[D]}{d\Delta{t}}\)

So, for the reaction: \(5Br^−(aq)+BrO^−_3(aq)+6H^+→3Br_2(aq)+3H_2O(l)\)

The rate would be: \(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}=- \frac{\Delta[BrO^-_3]}{\Delta{t}}= -\frac{\Delta[H^+]}{6\Delta{t}}=\frac{\Delta[Br_2]}{3\Delta{t}}=\frac{H_2O}{3\Delta{t}}\)

Step 2. Since we are given the rate for the disappearance of \(Br^-\)(aq) is \(3.5\times10^{-4} Ms^{-1}\), and we want to find the rate of appearance of \(Br_2\)(aq). Therefore we set the two rates equal to each other.

\(rate =- \frac{\Delta[Br^-]}{5\Delta{t}}= \frac{\Delta[Br_2]}{3\Delta{t}}\)

And,\(-\frac{\Delta[Br^-]}{\Delta{t}}= -3.5\times10^{-4} Ms^{-1}\)

So, \(3.5\times10^{-4} Ms^{-1}\) = \(\frac{5}{3}\frac{\Delta[Br_2]}{\Delta{t}}\)

Step 3. Now solve the equation.

\(\frac{(3.5\times10^{-4}Ms^{-1})(3)}{5} = \frac{\Delta[Br_2]}{\Delta{t}}\)

\(\frac{\Delta[Br_2]}{\Delta{t}} = 2.1 \times 10^{-4} Ms^{-1}\)

Exercise \(\PageIndex{5}\)**

Write a balanced equation for the reaction with this rate expression:

\(rate =- \frac{\Delta[\ce{SO2}]}{\Delta{t}}=- \frac{\Delta[\ce{CO}]}{3\Delta{t}}= \frac{\Delta[\ce{CO2}]}{2\Delta{t}}=\frac{\Delta[\ce{COS}]}{\Delta{t}}\nonumber\)

Answer

For the general reaction: aA + bB → cC+ dD

\(rate =- \frac{\Delta[A]}{a\Delta{t}}=- \frac{\Delta[B]}{b\Delta{t}}= \frac{\Delta[C]}{c\Delta{t}}=\frac{\Delta[D]}{d\Delta{t}}\)

Consequently, the sign determines whether the compound is a reactant (negative sign) or a product (positive sign), and the coefficient in the denominator (a, b, c, d) corresponds to the coefficient in the chemical equation. 

\[ \ce{SO2}+3\ce{CO}⟶2\ce{CO2}+\ce{COS} \nonumber \]

Exercise \(\PageIndex{6}\)**

A study of the rate of the reaction represented as \(2A⟶B\) gave the following data:

Time (s)	0.0	5.0	10.0	15.0	20.0	25.0	35.0
[A] (M)	1.00	0.952	0.625	0.465	0.370	0.308	0.230

1. Determine the average rate of disappearance of A between 0.0 s and 10.0 s, and between 10.0 s and 20.0 s.
2. Use the rate found in part (a) to determine the average rate of formation of B between 0.00 s and 10.0 s.

 

Answer

a) The change in A from 0s to 10s is 0.625M - 1M = -0.375M

so \(\frac{-\bigtriangleup A}{\bigtriangleup t}\) = 0.375M/10s = 0.0375 M/s

Similarly, the change in A from 10 to 20 seconds is 0.370M - 0.625M = -0.255M

so \(\frac{-\bigtriangleup A}{\bigtriangleup t}\) = 0.255M/(20s - 10s) = 0.0255 M/s

b) Using the equation \(\frac{-\bigtriangleup A}{2\bigtriangleup t}=\frac{\bigtriangleup B}{\bigtriangleup t}\), we divide the rate in part (a) in half to get 0.0188 M/s from 0 to 10 seconds.

Rate Law

Exercise \(\PageIndex{7}\)*

What is the order with respect to the following reactants?

1. Doubling the concentration of a reactant increases the rate of a reaction four times.
2. Tripling the concentration of a different reactant increases the rate of a reaction three times.

Answer

rate = k[reactant]^order

a) Since doubling the concentration increases the rate by a factor of four, the order (the exponent) must be 2. The reaction is second order with respect to the reactant.

b) Since tripling the concentration increases the rate by a factor of three, the order (the exponent) must be 1. The reaction is first order with respect to the reactant.

Exercise \(\PageIndex{8}\)*

How much and in what direction will each of the following affect the rate of the reaction: \(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) if the rate law for the reaction is \(\ce{rate}=k[\ce{NO2}]^2\)?

1. Decreasing the pressure of NO₂ from 0.50 atm to 0.250 atm.
2. Increasing the concentration of CO from 0.01 M to 0.03 M.

Answer

a. Decreasing the pressure by a factor of 2 will reduce the rate by a factor of 4 since the reaction is second order with respect to NO₂.

b. Since CO does not appear in the rate law increasing the concentration will have no effect on the rate.

Exercise \(\PageIndex{9}\)*

Regular flights of supersonic aircraft in the stratosphere are of concern because such aircraft produce nitric oxide, NO, as a byproduct in the exhaust of their engines. Nitric oxide reacts with ozone, and it has been suggested that this could contribute to the depletion of the ozone layer. The reaction \(\ce{NO + O3⟶NO2 + O2}\) is first order with respect to both NO and O₃ with a rate constant of 2.20 × 10⁷ M^-1s^-1. What is the rate of disappearance of NO when [NO] = 3.3 × 10⁻⁶ M and [O₃] = 5.9 × 10⁻⁷ M?

Answer

rate = k[NO][O₃]

rate = 2.20 x 10⁷ M^-1s^-1 (3.3 × 10⁻⁶ M)(5.9 × 10⁻⁷ M) = 4.3 x 10^-5 M/s

Exercise \(\PageIndex{10}\)*

The rate law for the following reaction

\[\ce{BrO3-}(aq)+\ce{5Br-}(aq)+\ce{6H+}(aq)⟶\ce{3Br2}(aq)+\ce{3H2O}(l)\nonumber\]

is \(rate =[\ce{BrO3-}][\ce{Br-}][\ce{H+}]^2 \). 

a. Give the reaction order with respect to each reactant and the overall reaction order.

b. By what factor does the rate change if \([\ce{BrO3-}]\) is doubled?

c. By what factor does the rate changes if \([\ce{Br-}]\) is halved?

d. By what factor does the rate change if \([\ce{H+}] \) is doubled?

Answer

a. In the rate equation, the orders are given by the exponents of the concentration terms. The overall order is the sum of the individual orders. Therefore, the reaction is:

• First order with respect to [BrO₃⁻]
• First order with respect to [Br⁻]
• Second order with respect to [H⁺]
• Overall reaction order = 1 + 1 + 2 = 4

b. Doubling [BrO₃⁻] (which is first order) would increase the rate by a factor of 2.

c. Halving [Br⁻] (which is first order) would decrease the rate by a factor of 1/2.

d. Doubling [H⁺] (which is second order) would increase the rate by a factor of 2² = 4.

Exercise \(\PageIndex{11}\)**

From the following data, determine the rate equation, the rate constant, and the order with respect to A for the reaction \(A⟶2C\).

[A] (M)	1.33 × 10^−2	2.66 × 10^−2	3.99 × 10^−2
Rate (M/h)	3.80 × 10^−7	1.52 × 10^−6	3.42 × 10^−6

Answer

A. Using the experimental data, we can compare the effects of changing [A] on the rate of reaction by relating ratios of [A] to ratios of rates

\[ \frac{2.66 \times 10^{-2}M}{1.33 \times 10^{-2}M} = 2\nonumber \] and \[ \frac{1.52 \times 10^{-6}M/h}{3.8 \times 10^{-7}M/h} = 4\nonumber \]

B. From this we know that doubling the concentration of A will result in quadrupling the rate of reaction. The order of this reaction is 2.

C. We can now write the rate equation since we know the order:

\[rate=k[A]^2\nonumber \]

D. By plugging in one set of experimental data into our rate equation we can solve for the rate constant, k:

\[3.80 \times 10^{-7}M/h = k \times (1.33 \times 10^{-2}M)^{2}\nonumber \]

\[k = \frac{3.80 \times 10^{-7}M/h}{1.769 \times 10^{-4}M^2}\nonumber \]

\[k= 0.00215 M^{-1}h^{-1}\nonumber \]

Exercise \(\PageIndex{12}\)**

Nitric oxide reacts with chlorine according to the equation:

\[\ce{2NO}(g)+\ce{Cl2}(g)⟶\ce{2NOCl}(g)\nonumber \]

The following initial rates of reaction have been observed for certain reactant concentrations:

[NO] (M)	[Cl2] (M)	Rate (M/h)
0.50	0.50	1.14
1.00	0.50	4.56
1.00	1.00	9.12

What is the rate law? What is the rate constant?

Answer

For the general equation,

\(aA + bB \rightarrow cC + dD\)

The rate can be written as

\(rate = k[A]^{m}[B]^{n}\) where k is the rate constant, and m and n are the reaction orders.

For our equation

\(2NO(g) + Cl_{2}(g) \rightarrow 2NOCl(g)\)

the \(rate = k[NO]^{m}[Cl_{2}]^{n}\)

Now, we need to find the reaction orders. Reaction orders can only be found through experimental values. We can compare two reactions where one of the reactants has the same concentration for both trials, and solve for the reaction order.

\(\frac{rate_{1}}{rate_{2}}=\frac{[NO]_{1}^{m}[Cl_{2}]_{1}^{n}}{[NO]_{2}^{m}[Cl_{2}]_{2}^{n}}\)

We can use the data in the table provided. If we plug in the values for rows 1 and 2, we see that the values for the concentration of Cl will cancel, leaving just the rates and the concentrations of NO.

\(\frac{1.14M/h}{4.56M/h}=\frac{[0.5M]^{m}}{[1.0M]^{m}}\)

We can now solve for m, and we find that m =2. This means that the reaction order for [NO] is 2.

Now we must find the value of n. To do so, we can use the same equation but with the values from rows 2 and 3. This time, the concentration of NO will cancel out.

\(\frac{4.56M/h}{9.12M/h}=\frac{[0.5M]^{n}}{[1.0M]^{n}}\)

When we solve for n, we find that n = 1. This means that the reaction order for [Cl₂] is 1.

We are one step closer to finishing our rate equation.

\(rate = k[NO]^{2}[Cl_{2}]\)

Finally, we can solve for the rate constant. To do this, we can use one of the trials of the experiment, and plug in the values for the rate, and concentrations of reactants, then solve for k.

\(1.14 M/h = k[0.5 M]^{2}[0.5 M]\)

\(k=9.12\; M^{-2}h^{-1}\)

So, our final rate equation is:

\(rate = (9.12\;M^{-2}h^{-1})[NO]^{2}[Cl_{2}]\)

*A common mistake is forgetting units. Make sure to track your units throughout the process of determining your rate constant. Be careful because the units will change relative to the reaction order.

Exercise \(\PageIndex{13}\)**

Under certain conditions, the decomposition of ammonia on a metal surface gives the following data:

[NH3] (M)	1.0 × 10^−3	2.0 × 10^−3	3.0 × 10^−3
Rate (M/h)	1.5 × 10^−6	1.5 × 10^−6	1.5 × 10^−6

Determine the rate law and the rate constant for this reaction.

Answer

In the three trials, the rate is the same despite [NH₃] changing.  This means that the reaction is zeroth order.

rate = k

k = 1.5 × 10⁻⁶ M/h

Exercise \(\PageIndex{14}\)**

Hydrogen reacts with nitrogen monoxide to form dinitrogen monoxide (laughing gas) according to the equation:

\[\ce{H2}(g)+\ce{2NO}(g)⟶\ce{N2O}(g)+\ce{H2O}(g)\nonumber \]

Determine the rate equation, the rate constant, and the orders with respect to each reactant from the following data:

[NO] (M)	0.30	0.60	0.60
[H2] (M)	0.35	0.35	0.70
Rate (M/s)	2.835 × 10^−3	1.134 × 10^−2	2.268 × 10^−2

Answer

To find the orders of each reactant, we see that when [NO] doubles but [H₂] doesn't change, the rate quadruples, meaning that the reaction is of second order with respect to [NO] ([NO]²). When [H₂] doubles but [NO] doesn't change, the rate doubles, meaning that [H₂] is a first order reactant.

Rate = k[NO]²[H₂]

We can use this rate law to determine the value of the rate constant. Plug in the data for reactant concentration and rate from one of the trials to solve for k, the rate constant. In this case, we chose to use the data from trial 1 from the second column of the data table.

2.835x10^-3 M/s= k[0.30M]²[0.35M]

k = 0.090 M^-2s^-1

Integrated Rate Laws

Exercise \(\PageIndex{15}\)*

Describe how graphical methods can be used to determine the order of a reaction and its rate constant from measurements of the concentration of A with time.

Answer

To determine the order of a reaction when given the data series, one must graph the data as it is, graph it as the natural log of [A], and graph it as 1/[A] versus time. Whatever method yields a straight line will determine the order. Respective of the methods of graphing above, if a straight line is yielded by the first graphing method, it is a 0th order; if by the second method, it's a 1st order; and if by the third graphing method, it's a 2nd order. When the order of the graph is known, a series of equations, given in the above image, can be used with the various points on the graph to determine the value of k. We can see that we need an initial value of A and a final value of A, and both of these would be given by the data.

Zeroth order, when plotting initial concentration versus final concentration, you have a negative linear slope.

\[[A] = [A]_0 − kt\nonumber \]

First order, when plotting ln[initial concentration] versus ln[final concentration], you have a negative linear slope.

\[\ln[A] = \ln[A]_0 − kt\nonumber \]

Second order, when plotting the 1/[initial concentration] versus 1/[final concentration], you have a positive linear slope.

\[\dfrac{1}{[\textrm A]}=\dfrac{1}{[\textrm A]_0}+kt\nonumber \]

Exercise \(\PageIndex{16}\)**

Use the graphs provided to determine the order of the following reaction: \(\ce{SO2Cl2 ⟶ SO2 + Cl2}\)

Time (s)	0	5.00 × 10^3	1.00 × 10^4	1.50 × 10^4	2.50 × 10^4	3.00 × 10^4	4.00 × 10^4
[SO2Cl2] (M)	0.100	0.0896	0.0802	0.0719	0.0577	0.0517	0.0415

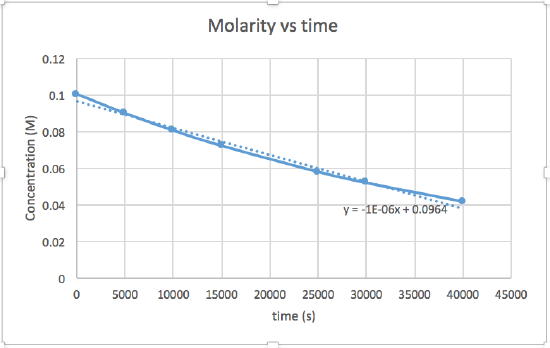
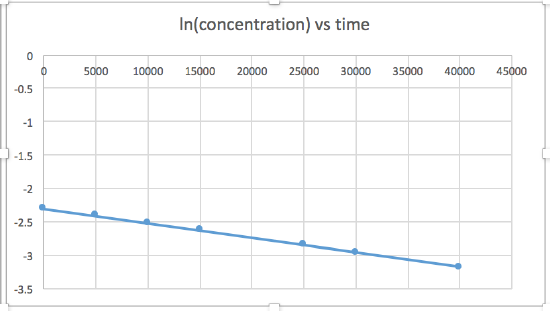
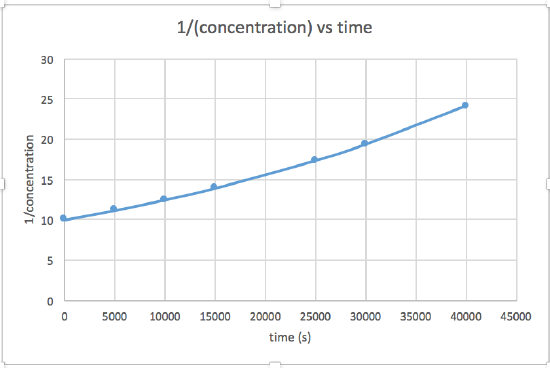
Answer

The plot of ln\([\ce{SO2Cl2}]\) vs time is linear, so the rate law is \(rate = k[\ce{SO2Cl2}]\)

Exercise \(\PageIndex{17}\)**

Suppose that the half-life of steroids taken by an athlete is 42 days. Assuming that the steroids biodegrade by a first-order process, how long would it take for \(\dfrac{1}{64}\) of the initial dose to remain in the athlete’s body?

Answer

Approach #1

1. Find out how many half-lives to get to 1/64th of initial dose:

\[1 \xrightarrow{t_{1/2}} \dfrac{1}{2}\xrightarrow{t_{1/2}} \dfrac{1}{4}\xrightarrow{t_{1/2}} \dfrac{1}{8}\xrightarrow{t_{1/2}} \dfrac{1}{16}\xrightarrow{t_{1/2}} \dfrac{1}{32}\xrightarrow{t_{1/2}} \dfrac{1}{64}\ \nonumber\]

2. Counting the number of half-lives, we see that it takes 6 half-lives to reach 1/64 of the initial concentration.  Since the half-life is constant for a first-order reaction, we can multiply 6 x 42 days = 252 days

Approach #2

1.  For a first order reaction, the integrated rate law is \(ln\dfrac{[A]_t}{[A]_0}=-kt\)

For the half-life, t = t_1/2 = 42 days and [A]_t = 0.5[A]₀ so we can find k.

\[ln\left(\dfrac{0.5[A]_0}{[A]_0}  \right)=-k(42\:days) \nonumber\]

k = 0.0165 days^-1

2.  We want the time when the [A]_t = 1/64[A]_0.

\[ln\left(\dfrac{\dfrac{1}{64}[A]_0}{[A]_0}  \right)=-0.0165days^{-1}t \nonumber\]

t = 252 days

Exercise \(\PageIndex{18}\)**

In a first-order reaction, 95% of the original amount of reactant decomposes in 122 minutes. What is the half-life of this reaction?

Answer

To determine the half-life of a first-order reaction, we first calculate the rate constant \(k\) using the integrated rate law:

\[ \ln\left(\frac{[A]_t}{[A]_0}\right) = -kt  \nonumber\]

We're told that 95% of the reactant has decomposed in 122 minutes, so 5% remains:

\[ [A]_t = 0.05[A]_0 \nonumber\]

\[ \ln\left(\frac{0.05[A]_0}{[A]_0}\right) = -k(122) \quad \Rightarrow \quad \ln(0.05) = -122k \nonumber\]

\[ -2.996 = -122k \quad \Rightarrow \quad k = \frac{2.996}{122} = 0.0246\ \text{min}^{-1} \nonumber\]

For the half-life, \(t = t_{1/2}\) and \([A]_t = 0.5[A]_0\):

\[ \ln\left(\frac{0.5[A]_0}{[A]_0}\right) = -(0.0246\ \text{min}^{-1})(t_{1/2}) \nonumber\]

\[ t_{1/2} = \frac{0.693}{0.0246} = 28.2\ \text{min} \nonumber\]

Exercise \(\PageIndex{19}\)**

The reaction of compound A to give compounds C and D was found to be second-order in A.

The rate constant for the reaction was determined to be 2.42 M^-1s^-1. If the initial concentration is 0.500 mol/L, what is the value of t_1/2?

Answer

The second-order integrated rate law is \(\dfrac{1}{[A]_t}=kt+\dfrac{1}{[A]_0}\)

For the half-life, t = t_1/2 and [A]_t = 0.5[A]₀.

\[\dfrac{1}{0.5(0.500M)}=2.42M^{-1}s^{-1}t_{1/2}+\dfrac{1}{(0.500M)} \nonumber\]

When we plug in the given information, we get:

\[t_{\frac{1}{2}}=\frac{1}{\frac{2.42L}{mol \cdot s}[0.500\frac{mol}{L}]}=0.826 s\nonumber \]

Notice that the units cancel out to seconds.

Exercise \(\PageIndex{20}\)**

For the past 10 years, the unsaturated hydrocarbon 1,3-butadiene \(\ce{(CH2=CH–CH=CH2)}\) has ranked 38th among the top 50 industrial chemicals. It is used primarily for the manufacture of synthetic rubber. It is isomeric with cyclobutene:

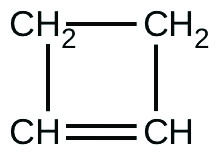
The isomerization of cyclobutene to butadiene is a first-order reaction, and the rate constant has been measured as 2.0 × 10⁻⁴ s⁻¹ at 150 °C in a 0.53-L flask. Determine the partial pressure of cyclobutene and its concentration after 30.0 minutes if an isomerization reaction is carried out at 150 °C with an initial pressure of 55 Torr.

Answer

For a first-order gas-phase reaction, the integrated rate law can be written using partial pressures:

\[ \ln\left(\frac{P_t}{P_0}\right) = -kt \nonumber\]

Given:

• \(P_0 = 55\ \text{Torr}\)
• \(k = 2.0 \times 10^{-4}\ \text{s}^{-1}\)
• \(t = 30.0\ \text{min} = 1800\ \text{s}\)

Substitute into the rate law:

\[ \ln\left(\frac{P_t}{55\ \text{Torr}}\right) = -0.36 \quad \Rightarrow \quad P_t = 55\ \text{Torr} \cdot e^{-0.36} = 38\ \text{Torr} \nonumber\]

To find the concentration of cyclobutene, use the ideal gas law:

\[ [\text{cyclobutene}] = \frac{n}{V} = \frac{P}{RT} = \frac{38\ \text{Torr} \cdot \frac{1\ \text{atm}}{760\ \text{Torr}}}{(0.08206\ \frac{\text{L·atm}}{\text{mol·K}})(423\ \text{K})} = 1.4 \times 10^{-3}\ \text{mol/L} \nonumber\]

Exercise \(\PageIndex{21}\)*

The reaction \(\ce{CO}(g)+\ce{NO2}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\) has the following rate law: \(\ce{rate}=k[\ce{NO2}]^2\).  If the [\(\ce{NO2}]\) changes from 1.35 x 10^-3 M to 1.29 x 10^-3 M in 10.0 s, what is the rate constant for the reaction?

Answer

The second order integrated rate law is \(\dfrac{1}{[A]_t}=kt+\dfrac{1}{[A]_0}\)

 

\(k=\dfrac{\left(\dfrac{1}{[A]_t}-\dfrac{1}{[A]_0}  \right)}{t}=\dfrac{\left(\dfrac{1}{1.29\times10^{-3}M}-\dfrac{1}{1.35\times10^{-3}M}  \right)}{10.0 s}=3.45\;M^{-1}s^{-1}\)

Collision Theory

Exercise \(\PageIndex{22}\)*

Chemical reactions occur when reactants collide. What are two factors that may prevent a collision from producing a chemical reaction?

Answer

The two factors that may prevent a collision from producing a chemical reaction are:

1. Kinetic energy of the reactants

In order for chemical reactions to occur, molecules require enough velocity to overcome the minimum activation energy needed to reach the transition state.

2. The orientation of molecules during the collision

Two molecules have to collide in the right orientation in order for the reaction to occur.

Exercise \(\PageIndex{23}\)*

How does an increase in temperature affect rate of reaction?

Answer

Collision theory states that the rates of chemical reactions depend on the fraction of molecules with the correct orientation, fraction of collisions with required energy, and the collision frequency. Because the fraction of collisions with required energy is a function of temperature, as temperature increases, the fraction of collisions with required energy also increases. The kinetic energy of reactants also increases with temperature which means molecules will collide more often increasing collisions frequency. With increased fraction of collisions with required energy and collisions frequency, the rate of chemical reaction increases. We see mathematically, from the Arrhenius equation, that temperature and the rate constant are related.

\[k=Ae^{-\frac {E_a}{RT}} \nonumber\]

where k is the rate constant, A is the frequency factor, R is 8.3145 \( \frac {J}{mol \cdot K}\), Ea is the reaction-specific activation energy in \( \frac {J}{mol}\), and T is temperature in K. We see from the equation that k is very sensitive to changes in temperature.

Exercise \(\PageIndex{24}\)**

For a reversible reaction, the enthalpy change of the forward reaction is 37 kJ/mol, and the activation energy of the forward reaction is 96 kJ/mol.

Determine the activation energy of the reverse reaction. Provide a sketch of the potential energy vs. the progress of the reaction.

Answer

Because the enthalpy change of the forward reaction is 37 kJ/mol, the products are 37 kJ/mol closer to the transition state than the reactants. The activation energy for the reverse reaction is \(\mathrm{96\,kJ/mol-37\,kJ/mol=59\,kJ/mol}\).

\(\mathrm{\Delta H=+37\,kJ/mol}\)
\(\mathrm{E_a(forward)=96\,kJ/mol}\)
\(\mathrm{E_a(reverse)=59\,kJ/mol}\)

Exercise \(\PageIndex{25}\)**

The rate constant for the decomposition of acetaldehyde (CH₃CHO) to methane (CH₄) and carbon monoxide (CO) in the gas phase is 1.1 × 10⁻² M^-1s^-1 at 703 K and 4.95 M^-1s^-1 at 865 K. Determine the activation energy for this decomposition.

Answer

When given two rate constants for the same reaction but at two different temperatures, the Arrhenius equation can be rewritten as:

\[ln (\frac{k_2}{k_1}) = \frac{E_a}{R} (\frac{1}{T_1} - \frac{1}{T_2}) \nonumber\]

In this problem, all the variables are given except for the E_a (activation energy).

k₁ = 1.1 × 10⁻² \( \frac {L}{mol \cdot s} \)

T₁ = 703 \(K\)

k₂ = 4.95 \( \frac {L}{mol \cdot s} \)

T₂ = 865 \(K\)

R = 8.314 \( \frac {J}{mol \cdot K} \) (Ideal Gas Constant)

Now plug in all these values into the equation, and solve for E_a.

\[ln (\frac{4.95\frac{L}{mol\cdot s}}{1.1 × 10^{-2}\frac{L}{mol\cdot s}}) = \frac{E_a}{8.314 \frac{J}{mol\cdot K}} (\frac{1}{703} - \frac{1}{865})\nonumber \]

E_a = 1.9 x 10⁵ J/mol or 190 kJ/mol

Exercise \(\PageIndex{26}\)**

An elevated level of the enzyme alkaline phosphatase (ALP) in the serum is an indication of possible liver or bone disorders. The level of serum ALP is so low that it is very difficult to measure directly. However, ALP catalyzes a number of reactions, and its relative concentration can be determined by measuring the rate of one of these reactions under controlled conditions. One such reaction is the conversion of p-nitrophenyl phosphate (PNPP) to p-nitrophenoxide ion (PNP) and phosphate ion. Control of temperature during the test is very important; the rate of the reaction increases 1.47 times if the temperature changes from 30 °C to 37 °C. What is the activation energy for the ALP–catalyzed conversion of PNPP to PNP and phosphate?

Answer

Using the Arrhenius equation:

\[ln (\frac{k_2}{k_1}) = -\frac{E_a}{R} (\frac{1}{T_2} - \frac{1}{T_1}) \nonumber\]

Since the rate of reaction increases 1.47 times, k₂/k₁ = 1.47.  Note that the temperatures must be converted to K.

\[E_a=-\dfrac{\ ln\left( \dfrac{k_2}{k_1} \right) R}{(\frac{1}{T_2} - \frac{1}{T_1})} \nonumber\]

\[E_a=-\dfrac{\ ln\left( 1.47 \right)\left(8.314\dfrac{J}{mol \cdot K}\right)}{(\frac{1}{310K} - \frac{1}{303K})}=4.30\times10^4J/mol \nonumber\]

Reaction Mechanisms

Exercise \(\PageIndex{27}\)*

Nitrogen(II) oxide, NO, reacts with hydrogen, H₂.  Here is a proposed mechanism:

\[\ce{2NO + H2 ⟶ N2 + H2O2\:(slow)}\nonumber \]

\[\ce{H2O2 + H2 ⟶ 2H2O\:(fast)}\nonumber \]

a. What is overall reaction?

b. Identify any intermediates.

c. What is the molecularity and rate law for each step?

d. Is the mechanism consistent with the experimentally determined rate law: rate = k[NO][H₂]?

Answer

a. Overall reaction:

Add the two steps and cancel the intermediate (\(\ce{H2O2}\)):

\[ \ce{2NO + H2 -> N2 + H2O2} \\ \ce{H2O2 + H2 -> 2H2O} \nonumber\]

Overall:

\[ \ce{2NO + 2H2 -> N2 + 2H2O} \nonumber\]

b. Intermediate: \(\ce{H2O2}\) (formed in Step 1 and consumed in Step 2)

c. Molecularity and rate laws:

• Step 1: Termolecular; rate = \(k_1[\ce{NO}]^2[\ce{H2}]\)
• Step 2: Bimolecular; rate = \(k_2[\ce{H2O2}][\ce{H2}]\)

d. Consistency with experimental rate law:

The rate-determining step of the mechanism suggests a rate law of \(k[\ce{NO}]^2[\ce{H2}]\), but the experimentally determined rate law is \(k[\ce{NO}][\ce{H2}]\).

Conclusion: The proposed mechanism is not consistent with the experimental rate law.

Exercise \(\PageIndex{28}\)**

The reaction of CO with Cl₂ gives phosgene (COCl₂), a pulmonary agent that was used in World War I. Use the mechanism shown here to complete the following exercises:

\(\ce{Cl2}(g) \xrightleftharpoons[k_{-1}]{k_1}\ce{2Cl}(g) \) (fast)

\(\ce{CO}(g)+\ce{Cl}(g)\xrightarrow{k_{2}}\ce{COCl}(g)\) (slow)

\(\ce{COCl}(g)+\ce{Cl}(g)\xrightarrow{k_{3}}\ce{COCl2}(g)\) (fast)

1. Write the overall reaction.
2. Identify all intermediates.
3. Write the rate law for each elementary reaction.
4. Write the overall rate law expression.

Answer

a. Overall reaction:

Add all the steps and cancel intermediates:

\[ \ce{Cl2 <=> 2Cl} \\ \ce{CO + Cl -> COCl} \\ \ce{COCl + Cl -> COCl2} \nonumber\]

Cancelling intermediates (\(\ce{2Cl}\) and \(\ce{COCl}\)):

\[ \ce{Cl2 + CO -> COCl2} \nonumber\]

b. Intermediates: \(\ce{Cl}\), \(\ce{COCl}\)

c. Rate law for each step:

• Step 1 (fast equilibrium):
  Forward: \( \text{rate}_{\text{fwd}} = k_1[\ce{Cl2}] \)
  Reverse: \( \text{rate}_{\text{rev}} = k_{-1}[\ce{Cl}]^2 \)
• Step 2 (slow): \( \text{rate} = k_2[\ce{CO}][\ce{Cl}] \)
• Step 3 (fast): \( \text{rate} = k_3[\ce{COCl}][\ce{Cl}] \)

d. Overall rate law:

Based on the slow (rate-determining) step:

\[ \text{rate} = k_2[\ce{CO}][\ce{Cl}] \nonumber\]

Eliminate the intermediate \(\ce{Cl}\) using the equilibrium from Step 1:

rate_for = rate_rev

\[ k_1[\ce{Cl2}] = k_{-1}[\ce{Cl}]^2 \Rightarrow [\ce{Cl}] = \sqrt{\frac{k_1}{k_{-1}}[\ce{Cl2}]}\nonumber \]

Substitute into the rate law:

\[ \text{rate} = k_2[\ce{CO}] \cdot \sqrt{\frac{k_1}{k_{-1}}[\ce{Cl2}]} = k[\ce{CO}]\sqrt{[\ce{Cl2}]}\nonumber \]

Exercise \(\PageIndex{29}\)*

Consider the following reaction energy diagram:

a. How many elementary steps are in the mechanism?

b. Which step is the rate-determining step?

c. What do B and D correspond to?

d. What does C correspond to?

e. Is the overall reaction exothermic or endothermic?

Answer

a. There are 2 elementary steps, indicated by the two peaks (activation energy barriers) in the diagram.

b. The first step is the rate-determining step because it has the highest activation energy (the tallest peak).

c. B and D are transition states: high-energy, unstable configurations that occur at the peak of each step.

d. C is a reaction intermediate.  It forms in the first step and is consumed in the second, appearing in the valley between the two peaks.

e. The reaction is endothermic because the energy of the products (E) is higher than the energy of the reactants (A), indicating that energy is absorbed overall.

Catalysis

Exercise \(\PageIndex{30}\)*

Consider the following mechanisms.

a. \[\ce{O3 \xrightarrow{sunlight} O2 + O}\\ \ce{O3 + Cl ⟶ O2 + ClO}\\ \ce{ClO + O ⟶ Cl + O2}\nonumber \]

b. \[\ce{O3 \xrightarrow{sunlight} O2 + O\\ O3 + NO ⟶ NO2 + O2\\ NO2 + O ⟶ NO + O2}\nonumber \]

For each, give the overall reaction and identify any intermediates and any catalysts.

Answer

a.

\[\ce{O3 \xrightarrow{sunlight} O2 + \cancel{O}}\\ \ce{O3} + \cancel{\ce{Cl}} ⟶ \ce{O2} + \cancel{\ce{ClO}}\\ \cancel{\ce{ClO}} + \cancel{\text{O}} ⟶ \cancel{\ce{Cl}} + \ce{O2}\nonumber \]

overall: \[\ce{2O3} ⟶ \ce{3O2}\nonumber \]

Intermediates: O, ClO (both are made and then used up in a later step)

Catalyst: Cl (used in step 2 and reformed in step 3)

b. \[\ce{O3} \xrightarrow{sunlight} \ce{O2} + \cancel{\ce{O}}\\ \ce{O3} + \cancel{\ce{NO}} ⟶ \cancel{\ce{NO2}} + \ce{O2}\\ \cancel{\ce{NO2}} + \cancel{\ce{O}} ⟶ \cancel{\ce{NO}} + \ce{O2}\nonumber \]overall: \[\ce{2O3} ⟶ \ce{3O2}\nonumber \]

Intermediates: O, NO₂

Catalyst: NO

Additional Problems

Exercise \(\PageIndex{31}\)***

Experiments were conducted to study the rate of the reaction represented by this equation.

\[\ce{2NO}(g)+\ce{2H2}(g)⟶\ce{N2}(g)+\ce{2H2O}(g)\nonumber \]

Initial concentrations and rates of reaction are given here.

Experiment	Initial Concentration [NO] (mol/L)	Initial Concentration, [H2] (mol/L)	Initial Rate of Formation of N2 (M/ min)
1	0.0060	0.0010	1.8 × 10^−4
2	0.0060	0.0020	3.6 × 10^−4
3	0.0010	0.0060	0.30 × 10^−4
4	0.0020	0.0060	1.2 × 10^−4

Consider the following questions:

1. Determine the order for each of the reactants, NO and H₂, from the data given and show your reasoning.
2. Write the overall rate law for the reaction.
3. Calculate the value of the rate constant, k, for the reaction. Include units.
4. What is the initial rate when [NO] = 0.0015 M and [H₂]=0.0035M?
5. The following sequence of elementary steps is a proposed mechanism for the reaction.

Step 1: \(\ce{NO + NO} \xrightleftharpoons[k_{-1}]{k_1}\ce{N2O2} \:(fast)\)

Step 2: \(\ce{N2O2 + H2 \xrightarrow{k_{2}} H2O + N2O} \:(slow)\)

Step 3: \(\ce{N2O + H2 \xrightarrow{k_{3}} N2 + H2O} \:(fast)\)

Show that the mechanism is consistent with the observed rate law for the reaction and the overall stoichiometry of the reaction.

Answer

a.  In comparing trials 1 and 2, we see that [NO] is constant.  The [H₂] doubles, as does the rate, so the reaction is of first order with respect to H₂.

In comparing trials 3 and 4, the [H₂] is constant.  The [NO] doubles, while the rate increases by a factor of 4, so the reaction is of second order with respect to NO.

b. rate = k[NO]²[H₂]

c. Using the data from Trial 1:

\[rate=k[\ce{NO}]^2[\ce{H2}]\\k=\dfrac{rate}{[\ce{NO}]^2[\ce{H2}]}=\dfrac{1.8\times10^{-4}M/min}{(0.0060M)^2(0.0010M)}=5000 M^{-2}min^{-1}\nonumber \]

d. \[rate=k[\ce{NO}]^2[\ce{H2}]=5000 M^{-2}min^{-1}(0.0015M)^2(0.0035M)=3.9\times10^{-5}M/min\nonumber \]

e. The overall reaction described by the mechanism matches the reaction:

\[\ce{2NO}(g)+\ce{2H2}(g)⟶\ce{N2}(g)+\ce{2H2O}(g)\nonumber \]

The rate law is based on the slow step:

rate = k₂[N₂O₂][H₂]

N₂O₂ is an intermediate, so we need to use step 1 to write in terms of reactants.

rate_for = rate_rev

k₁[NO]² = k_-1[N₂O₂]    [N₂O₂]=k₁/k_-1[NO]²

rate = k₁k₂/k_-1[NO]²[H₂] This matches the experimentally determined rate law.

Exercise \(\PageIndex{32}\)**

Draw a reaction energy diagram consistent with the mechanism:

Step 1: \(\ce{NO + NO} \xrightleftharpoons[k_{-1}]{k_1} \ce{N2O2} \:(fast) \)

Step 2: \(\ce{N2O2 + H2 \xrightarrow{k_{2}} H2O + N2O} \:(slow) \)

Step 3: \(\ce{N2O + H2 \xrightarrow{k_{3}} N2 + H2O} \:(fast) \)

The overall reaction is exothermic.

Answer

The reaction energy diagram should have three peaks to represent the transition states for the three steps in the mechanism. The activation energy of the second step should be the largest because it is the slow (rate-determining) step. The first and third steps are fast, so their activation energies are relatively low. In particular, the first step is a fast equilibrium, which means the activation energy is low in both the forward and reverse directions. The products should be lower in energy than the reactants because the overall reaction is exothermic.

Exercise \(\PageIndex{33}\)***

Hydrogen iodide, HI, decomposes in the gas phase to produce hydrogen, H₂, and iodine, I₂. The value of the rate constant, k, for the reaction was measured at two different temperatures, and the data are shown here:

Temperature (K)	k (M^−1 s^−1)
555	6.23 × 10^−7
575	2.42 × 10^−6
700	?

What is the value of the activation energy (in kJ/mol) for this reaction?  What is the rate constant at 700 K?

Answer

Find the activation energy by using the Arrhenius equation with the data from trials 1 and 2:

\[ \ln\left(\frac{k_2}{k_1}\right) = -\frac{E_a}{R} \left(\frac{1}{T_2} - \frac{1}{T_1}\right) \nonumber\]

\[ E_a = \frac{-R \cdot \ln\left(\frac{2.42 \times 10^{-6}}{6.23 \times 10^{-7}}\right)}{\left(\frac{1}{575} - \frac{1}{555}\right)} = \frac{-8.314\ \text{J/mol·K} \cdot \ln(3.884)}{-6.238 \times 10^{-5}\ \text{K}^{-1}} = 1.80 \times 10^5\ \text{J/mol} \nonumber\]

\[ E_a = 180\ \text{kJ/mol} \nonumber\]

We can find the rate constant at 700 K by using the Arrhenius equation once again, now with the calculated value of the activation energy. Here, trials 1 and 3 are compared, but the same procedure can be done for trials 2 and 3:

\[ \ln\left(\frac{k_3}{6.23 \times 10^{-7}}\right) = -\frac{1.80 \times 10^5\ \text{J/mol}}{8.314\ \text{J/mol·K}} \left(\frac{1}{700} - \frac{1}{555}\right) \nonumber\]

\[ \ln\left(\frac{k_3}{6.23 \times 10^{-7}}\right) = 8.08 \nonumber\]

\[ \frac{k_3}{6.23 \times 10^{-7}} = e^{8.08} = 3229 \nonumber\]

\[ k_3 = 6.23 \times 10^{-7} \times 3229 = 2.01 \times 10^{-3}\ \text{M}^{-1}\text{s}^{-1} \nonumber\]

Exercise \(\PageIndex{34}\)***

Consider the following mechanism:

Step 1: \(\ce{W + W} \xrightleftharpoons[k_{-1}]{k_1}\ce{A} \:(fast) \)

Step 2: \(\ce{A + X \xrightarrow{k_{2}} Y + B} \:(slow) \)

Step 3: \(\ce{B + X \xrightarrow{k_{3}} Z} \:(fast) \)

a. What is the overall reaction?

b. Which step is the rate-determining step?

c. What is the rate law for the reaction?

d. What is the effect on the reaction rate of doubling the [W] and halving the concentration of [X]?

Answer

a. 2W + 2X ⟶ Y + Z

b. The slow step is rate-determining, so step 2.

c. The rate law is based on the slow step:

rate = k₂[A][X]

A is an intermediate, so we need to use step 1 to write in terms of reactants.

rate_for = rate_rev

k₁[W]² = k_-1[A]    [A]=k₁/k_-1[W]²

rate = k₁k₂/k_-1[W]²[X]

d. Doubling [W] would increase the rate by a factor of 4. Halving [X] would halve the rate. Together, these changes would cause the rate to double.

Exercise \(\PageIndex{35}\)**

The following data have been determined for the reaction:

\[\ce{I- + OCl- ⟶ IO- + Cl-}\nonumber \]

	1	2	3
\(\mathrm{[I^-]_{initial}}\) (M)	0.10	0.20	0.30
\(\mathrm{[OCl^-]_{initial}}\) (M)	0.050	0.050	0.010
Rate (M/s)	3.05 × 10^−4	6.10 × 10^−4	1.83 × 10^−4

Determine the rate equation and the rate constant for this reaction.

Answer

rate = k[I^-]^m[OCl^-]ⁿ

In comparing Trials 1 and 2 the [OCl^-] is constant.  The [I^-] doubles and rate also doubles, so the reaction is first order with respect to I^-.  m = 1.

We cannot "cross out" \([I^-]\) to find n because no two trials have the same concentration of I^-. In order to find the reaction order for we need to use m = 1.

\[ \frac {rate_1}{rate_3} = \frac {(0.10M)^{1}(0.050M)^n)}{(0.30M)^{1}(0.010M)^n)} = \frac {3.05 \times 10^{-4}M/s}{1.83 \times 10^{-4}M/s} \nonumber\]

\[ \frac {1}{3} (5^{n}) = 1.6666667 \nonumber\]

\[ 5^{n} = 5 \nonumber\]

\[ n = 1 \nonumber\]

\[ rate=k[OCl^-][I^-] \nonumber\]

\[ 3.05 \times 10^{-4}M/s= k(0.05M)(0.10M)\nonumber \]

\[ k = 6.1 \times 10^{-2} M^{-1}s^{-1} \nonumber\]

Exercise \(\PageIndex{36}\)**

Cyclopropane is used as an anesthetic:

When heated to 499 °C, cyclopropane undergoes a first-order rearrangement with a rate constant of 5.95 × 10⁻⁴ s⁻¹. What is the half-life of this reaction in hours? What fraction of the cyclopropane remains after 0.75 h at 499 °C?

Answer

For a first-order reaction, the integrated rate law is \(ln\dfrac{[A]_t}{[A]_0}=-kt\)

For the half-life, t = t_1/2, [A]_t = 0.5[A]₀. With k=5.95 × 10⁻⁴ s⁻¹:

\[ln\left(\dfrac{0.5[A]_0}{[A]_0}  \right)=-(5.95 \times 10^{-4}s^{-1})t_{1/2} \nonumber\]

t_1/2 = 1165 s

\[1165s\left(\dfrac{1min}{60s}\right)\left(\dfrac{1h}{60min}\right)=0.324h \nonumber \]

To find amount remaining after 0.75 h, first convert to s:

\[0.75h\left(\dfrac{60min}{1h}\right)\left(\dfrac{60s}{1min}\right)=2700s \nonumber\]

\[ln\dfrac{[A]_t}{[A]_0}=-(5.95 \times 10^{-4}s^{-1})(2700s)=1.61\nonumber\]

\[\dfrac{[A]_t}{[A]_0}=e^{-1.61}=0.20 \nonumber\]

This means that the [A]_0.75h=0.20[A]₀ which means that 20% of the cyclopropane remains after 0.75 h.

Exercise \(\PageIndex{37}\)**

The overall reaction \(\ce{H2 + Br2 \rightarrow 2HBr}\) occurs in the following three step mechanism:

1. \(\mathrm{Br_2 \xrightleftharpoons[k_{-1}]{k_1} 2Br\: (forward\: and\: reverse\: reactions\: are\: fast)}\)
2. \(\mathrm{ Br+H_2 \xrightarrow{k_2} HBr+H\:(slow)}\)
3. \(\mathrm{H+Br_2 \xrightarrow{k_3} HBr+Br \:(fast)}\)

What is the rate law for the entire reaction?

Answer

Because step ii is the slow step, it is the rate-determining step, and the rate law should be derived according to it.

\(rate=k_2[Br][H_2]\)

Br is an intermediate, so we need to find an expression for [Br] in terms of reactants by using the first fast equilibrium step:

rate_for = rate_rev

\(\mathrm{k_1[Br_2]=k_{-1}[Br]^2}\), \(\mathrm{[Br]=\left(\dfrac{k_1}{k_{-1}}\right)^{1/2}[Br_2]^{1/2}}\)

We can now replace \(\ce{[Br]}\) in the original rate law expression, giving:

\(\mathrm{rate=k_2\left(\dfrac{k_1}{k_{-1}}\right)^{1/2}[H_2][Br_2]^{1/2}}\)

Exercise \(\PageIndex{38}\)**

The reaction A + B  ⟶ C + D is second-order in A and zero-order in B.  The value of the rate constant k is 0.0107 M^-1 min^-1. What is the rate of this reaction when [A] = 0.0010 M and [B] = 0.25 M?

Answer

rate = k[A]²[B]⁰= k[A]²=0.0107 M^-1 min^-1(0.0010M)²=1.07 x 10^-8 M/min