5.7: Bond Energies

Learning Objectives

• Use average covalent bond energies to estimate enthalpies of reaction

As we saw in Chapter 3, stable molecules exist because the atoms together have a lower energy than the same atoms apart. Covalent bonds hold atoms together within molecules. Breaking those bonds requires energy, and forming new ones releases energy. During a chemical reaction, some bonds in the reactants are broken (which requires energy), and new bonds in the products are formed (which releases energy). Whether the overall reaction is exothermic or endothermic depends on the relative amounts of energy used and released.

The strength of a covalent bond is measured by the energy required to break it. The bond energy or bond dissociation energy is the amount of energy required to break one mole of a specific bond in gaseous molecules under standard conditions. For example:
\[\ce{H_2(g) \longrightarrow 2 H (g)} \quad  \quad D_{\ce{H-H}}=\Delta H^{\circ}=436\,\text{kJ/mol} \nonumber \]

This means it takes 436 kJ to break one mole of H–H bonds in hydrogen gas. Note that this value applies to molecules in the gas phase, and it reflects the energy required to separate the bonded atoms completely. Because energy is required to break a bond, bond energies are always positive values.

Molecules with multiple atoms have many covalent bonds. For example, methane (CH₄) contains four C–H bonds. Breaking all of them requires 1660 kJ per mole of methane:

Dividing by four, we estimate the average bond energy of a C-H bond as 1660/4 = 415 kJ/mol. This is an average because each bond doesn’t necessarily require the same amount of energy to break. After the first bond is broken, the structure of the molecule changes, which can make the other bonds easier or harder to break. Bond energies used in tables are averages taken from many compounds, not precise values for a single molecule.

The strength of a bond depends on how strongly the two atoms attract the shared electrons. In general, the more electron pairs shared between two atoms, the stronger the bond. Triple bonds are stronger (and shorter) than double bonds. Double bonds are stronger (and shorter) than single bonds. This trend applies when the same two elements form different types of bonds.

Bond strength is also affected by which elements are bonded together. When comparing a series of bonds between carbon and different halogens, the bond strength decreases down the group. For example:

    C–F: 439 kJ/mol

    C–Cl: 330 kJ/mol

    C–Br: 275 kJ/mol

This is because larger atoms form longer bonds, which are generally weaker.

Average bond energies for common bonds are listed in Table \(\PageIndex{1}\), and a comparison of bond lengths and bond strengths for some common bonds appears in Table \(\PageIndex{2}\).

Table \(\PageIndex{1}\): Bond Energies (kJ/mol)

Bond	Bond Energy	Bond	Bond Energy	Bond	Bond Energy
H–H	436	C–S	260	F–Cl	255
H–C	415	C–Cl	330	F–Br	235
H–N	390	C–Br	275	Si–Si	230
H–O	464	C–I	240	Si–P	215
H–F	569	N–N	160	Si–S	225
H–Si	395	\(\ce{N=N}\)	418	Si–Cl	359
H–P	320	\(\ce{N#N}\)	946	Si–Br	290
H–S	340	N–O	200	Si–I	215
H–Cl	432	N–F	270	P–P	215
H–Br	370	N–P	210	P–S	230
H–I	295	N–Cl	200	P–Cl	330
C–C	345	N–Br	245	P–Br	270
\(\ce{C=C}\)	611	O–O	140	P–I	215
\(\ce{C#C}\)	837	\(\ce{O=O}\)	498	S–S	215
C–N	290	O–F	160	S–Cl	250
\(\ce{C=N}\)	615	O–Si	370	S–Br	215
\(\ce{C#N}\)	891	O–P	350	Cl–Cl	243
C–O	350	O–Cl	205	Cl–Br	220
\(\ce{C=O}\)	741	O–I	200	Cl–I	210
\(\ce{C#O}\)	1080	F–F	160	Br–Br	190
C–F	439	F–Si	540	Br–I	180
C–Si	360	F–P	489	I–I	150
C–P	265	F–S	285

Table \(\PageIndex{2}\): Average Bond Lengths and Bond Energies for Some Common Bonds

Bond	Bond Length (Å=0.1 nm)	Bond Energy (kJ/mol)
C–C	1.54	345
\(\ce{C=C}\)	1.34	611
\(\ce{C#C}\)	1.20	837
C–N	1.43	290
\(\ce{C=N}\)	1.38	615
\(\ce{C#N}\)	1.16	891
C–O	1.43	350
\(\ce{C=O}\)	1.23	741
\(\ce{C#O}\)	1.13	1080

We can use bond energies to estimate the enthalpy change of a reaction by comparing the energy needed to break bonds in the reactants to the energy released as new bonds form in the products.

\[\Delta H \approx \sum D_{\text {bonds broken }}-\sum D_{\text {bonds formed }} \nonumber \]

• Breaking bonds requires energy (positive values)

• Forming bonds releases energy (subtract from the total)

Consider the following reaction:

\[\ce{H2(g) + Cl2(g) -> 2 HCl(g)} \nonumber \]

Bonds broken:

• 1 H-H bond: 436 kJ/mol
• 1 Cl-Cl bond: 243 kJ/mol

Bonds formed:

• 2 H-Cl bonds: 2(432 kJ/mol) = 864 kJ/mol

\[\begin{align*}
\Delta H & \approx  \sum D_{\text{bonds broken}} - \sum D_{\text{bonds formed}} \\[4pt]
& \approx\left[ D_{\ce{H-H}} + D_{\ce{Cl-Cl}} \right] - 2 D_{\ce{H-Cl}} \\[4pt]
& \approx[436\,\text{kJ/mol}+243\,\text{kJ/mol}]- 2(432\,\text{kJ/mol}) \\[4pt] &=-185\,\text{kJ/mol}
\end{align*} \]

The reaction is exothermic because the bonds formed in the products are stronger than the bonds broken in the reactants. This value is in good agreement with the ΔH calculated using the ΔH_f^o(HCl) (\(\Delta H^o_f\)(HCl) = −92.3 kJ/mol, so ΔH^o = 2(−92.3 kJ/mol) = –184.6 kJ/mol).

This approach gives a good estimate of the enthalpy change, especially for reactions where enthalpies of formation are unavailable. However, it does not account for all factors that affect the energy of a chemical reaction:

•     Bond energies are averages, not exact values for a given molecule.
•     It does not include intermolecular forces, such as hydrogen bonding or dipole interactions, which may be present before or after the reaction.
•     It does not account for phase changes (e.g., condensation or vaporization) or differences in molecular structure and resonance.
•     It assumes all substances are in the gas phase, because bond energies are measured for gas-phase molecules.

For more accurate results, we use standard enthalpies of formation or experimental data.

Example \(\PageIndex{1}\): Using Bond Energies to Calculate Approximate Enthalpy Changes

Methanol, CH₃OH, is being explored as a cleaner alternative fuel. It can be produced from a mixture of carbon monoxide (CO) and hydrogen gas (H₂), which is made by reacting steam with carbon at high temperatures.

Using the bond energies in Table \(\PageIndex{2}\), estimate the enthalpy change, ΔH, for the following reaction:

\[\ce{CO(g) + 2 H2(g) -> CH3OH (g)} \nonumber \]

Compare this value to the ΔH calculated using heats of formation from the reference table.

Solution

First, we need to write the Lewis structures of the reactants and the products:

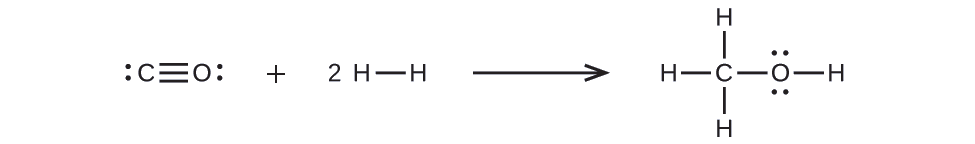
From this, we see that ΔH for this reaction involves the energy required to break a C–O triple bond and two H–H single bonds, as well as the energy produced by the formation of three C–H single bonds, a C–O single bond, and an O–H single bond. We can express this as follows:

\[\begin{aligned}
\Delta H & \approx\Sigma D_{\text {bonds broken }}-\Sigma D_{\text {bonds formed }} \\[4pt]
& \approx\left[ D_{ C \equiv O }+2\left( D_{ H - H }\right)\right]-\left[3\left( D_{ C - H }\right)+ D_{ C - O }+ D_{ O - H }\right]
\end{aligned} \nonumber \]

Using the bond energy values in Table \(\PageIndex{2}\), we obtain:

\[\begin{aligned}
\Delta H & \approx[1080+2(436)]-[3(415)+350+464] \\[4pt]
& \approx-107 kJ/mol
\end{aligned} \nonumber \]

We can compare this value to the value calculated based on heats of formation from the reference table:

\[\begin{aligned}
\Delta H & =\left[\Delta H_{ f }^{\circ} \ce{(CH_3 OH (g))}\right]-\left[\Delta H_{ f }^{\circ}\ce{( CO (g))}+2 \times \Delta H_{ f }^{\circ}\ce{( H_2)}\right] \\[4pt]
& =[-201.0\,\text{kJ/mol}]-[-110.5\,\text{kJ/mol}+2 \times 0] \\[4pt]
& =-90.5 \,\text{kJ/mol}
\end{aligned} \nonumber \]

There is a noticeable difference between the two results. This is expected, because using bond energies gives only an approximate value. Bond energies are average values taken from many different compounds, and this method does not account for factors like intermolecular forces and phase changes. The value calculated using standard enthalpies of formation is more accurate and reflects real experimental data.

Exercise \(\PageIndex{1}\)

Ethyl alcohol (ethanol), CH₃CH₂OH, was one of the first organic chemicals deliberately synthesized by humans. It has many uses in industry, and it is the alcohol contained in alcoholic beverages. It can be obtained by the fermentation of sugar or synthesized by the hydration of ethylene in the following reaction:

Using the bond energies in Table \(\PageIndex{2}\), calculate an approximate enthalpy change, ΔH, for this reaction.

Answer

Only the bonds that change during the reaction are included in the estimate; all other bonds are unchanged and cancel out.

\[\begin{aligned}
\Delta H & \approx \Sigma D_{\text {bonds broken }}-\Sigma D_{\text {bonds formed }} \\[4pt]
& \approx\left[ D_{ C=C }+\left( D_{ O - H }\right)\right]-\left[ D_{ C - H }+ D_{ C - C }+ D_{ C - O }\right]\\[4pt]
& \approx[611\,\text{kJ/mol}+464\,\text{kJ/mol}]-[415\,\text{kJ/mol}+345\,\text{kJ/mol}+350\,\text{kJ/mol}]\\[4pt]
& \approx-35\,\text{kJ/mol}
\end{aligned} \nonumber \]

Summary

Bond energy is the energy needed to break a specific bond in a gaseous molecule. Because bond energy values are often averaged across many compounds, they provide useful estimates but not exact values for individual molecules. Bond energies can be used to estimate the enthalpy change of a reaction by subtracting the energy released from forming product bonds from the energy used to break reactant bonds. This method is useful when standard enthalpies of formation are not available, but it has limitations and works best for gas-phase reactions.