5.E: Thermochemistry (Exercises)

Energy and Its Conversion

Exercise \(\PageIndex{1}\)*

Why does hammering a piece of sheet metal cause the metal to heat up?

Answer

When the hammer strikes the metal, its kinetic energy (energy of motion) is transferred to the metal. Some of this energy causes the atoms in the metal to vibrate more rapidly, which increases the thermal energy of the metal. As a result, the metal heats up.

Exercise \(\PageIndex{2}\)**

What is the difference between heat and temperature?

Answer

• Temperature is a measure of how hot or cold something is—it reflects the average kinetic energy of the particles in a substance.
• Heat is the transfer of energy from one object to another because of a difference in temperature.
• Heat flows from the hotter object to the cooler one until their temperatures are equal.

Exercise \(\PageIndex{3}\)*

Is each of the following a form of kinetic or potential energy? Explain your reasoning.
a) The attraction between opposite charges in an ionic bond
b) A gas molecule moving through the air

Answer

a) Potential energy – The opposite charges are attracted to each other; this energy is stored in the arrangement.
b) Kinetic energy – The gas molecule is in motion.

The First Law of Thermodynamics

Exercise \(\PageIndex{4}\)*

Explain the sign convention for describing the internal energy of the system with respect to heat and work.

Answer

In thermodynamics, we use a system-surroundings perspective. The change in internal energy of the system (ΔE) depends on heat (q) and work (w): ΔE = q + w

• Heat added to the system → q is positive
• Heat lost by the system → q is negative
• Work done on the system (e.g., compression) → w is positive
• Work done by the system (e.g., expansion) → w is negative

This sign convention means that if the system gains energy, ΔE is positive. If it loses energy, ΔE is negative.

Exercise \(\PageIndex{5}\)*

What is the change in internal energy (ΔE) of a system that releases 325 J of heat and has 12 J of work done on it?

Answer

The system releases heat, so q = -325 J.

Work is done on the system, so w = +12 J.

ΔE = q + w = -325 J + 12 J = -313 J.

The internal energy of the system decreases by 313 J.

Exercise \(\PageIndex{6}\)**

Refer to the figure below, which shows a chemical reaction between a copper penny and concentrated nitric acid. The reaction produces NO₂ gas, which causes the piston to move upward, keeping the pressure constant.

a. Is the system doing work on the surroundings or is work being done on the system? Explain.

b. Would the value of w be positive or negative for this reaction? Explain.

(a) Initially, the system (a copper penny and concentrated nitric acid) is at atmospheric pressure. (b) When the penny is added to the nitric acid, NO₂ gas that is formed causes the piston to move upward to maintain the system at atmospheric pressure.

Answer

a. The system is doing work on the surroundings. As NO₂ gas forms, it pushes the piston upward, which requires energy. This means energy is being transferred from the system to the surroundings in the form of work.

b. The value of w is negative, because in thermodynamics, work done by the system (expansion against a constant pressure) is defined as negative. The system loses energy as it pushes the piston upward.

Exercise \(\PageIndex{7}\)*

Argon gas expands from 3.25 L to 4.82 L against a constant external pressure of 2.30 atm.  Calculate the work done by the gas, in joules.

Answer

\(w = -P \Delta V = -2.30\:atm \cdot (4.82\:L - 3.25\:L) \cdot \left(\frac{101.32\:J}{L·atm} \right)=-366\:J \)

The negative sign means the gas did work on the surroundings by expanding.

Exercise \(\PageIndex{8}\)*

A sample of helium gas is compressed from 6.10 L to 2.75 L at a constant external pressure of 1.85 atm.  Calculate the work done on the gas, in joules.

Answer

\(w = -P \Delta V = -1.85\:atm \cdot (2.75\:L - 6.10\:L) \cdot \left(\frac{101.32\:J}{L·atm} \right)=+628\:J \)

The positive sign means work was done on the gas by the surroundings during compression.

Enthalpy

Exercise \(\PageIndex{9}\)*

A scientist placed an unknown salt in a small amount of water in a beaker. All the salt dissolved in the water, and the temperature of the solution dropped several degrees.

a. What is the sign of q for this reaction?

b. What is the sign of the enthalpy change (ΔH) for this reaction?

c. Is the dissolution exothermic or endothermic?

Answer

a. The temperature of the solution dropped, which means the surroundings (the water) lost heat. That heat was absorbed by the system (the dissolving salt), so q for the reaction is positive.

b. Because the process occurs at constant pressure, the heat flow q is equal to the change in enthalpy. So, the enthalpy change ΔH is also positive.

c. Since heat is absorbed by the system from the surroundings, the dissolution is endothermic.

Exercise \(\PageIndex{10}\)*

Heat is the flow of energy from one object to another due to a difference in temperature. Describe the direction of energy flow in:

 a. an exothermic reaction

 b. an endothermic reaction

Answer

a. In an exothermic reaction, heat flows from the system to the surroundings.

b. In an endothermic reaction, heat flows from the surroundings to the system.

Exercise \(\PageIndex{11}\)*

State whether the process is endothermic or exothermic.

a. Water is added to sodium hydroxide pellets, and the flask becomes hot.
b. Ammonium nitrate crystals are dissolved in water, causing the solution to become cool.

Answer

a. Exothermic. The system releases heat to the surroundings, making the flask feel hot.

b. Endothermic. The system absorbs heat from the surroundings, causing the solution to feel cool.

Exercise \(\PageIndex{12}\)*

Given the following thermochemical equation, what is ΔH for the reverse reaction?

N₂ (g) + 3H₂ (g) → 2NH₃ (g)     ΔH = -91.8 kJ/mol

Answer

If the direction of a chemical equation is reversed, the sign of ΔH also reverses.

ΔH = 91.8 kJ/mol

Exercise \(\PageIndex{13}\)*

Given the following thermochemical equation,

C₆H₆ (l) → 3C₂H₂ (g)       ΔH = 630.0 kJ/mol

a. Write the complete thermochemical equation for the reverse reaction.

b. What is ΔH for the following reaction?

6C₂H₂ (g) → 2C₆H₆ (l)

Answer

a.   3C₂H₂ (g) → C₆H₆ (l)       ΔH = -630.0 kJ/mol

b. The given reaction is twice the reverse reaction, so we also double the enthalpy change:

ΔH = 2(-630.0 kJ/mol) = -1260.0 kJ/mol

Exercise \(\PageIndex{14}\)**

Consider the formation of hydrogen gas from the following reaction:

\[\ce{2H2O (g) \rightarrow 2H2(g) + O2 (g)} \quad \Delta H^{\circ}=+483.6\,\text{kJ/mol} \nonumber\]

How much heat is involved in the formation of 35.0 mL of H₂ gas at 1.00 atm and 350 K?  Is the heat absorbed or released?

Answer

Step 1: Use the ideal gas law to find the moles of H₂:

\[n=\frac{PV}{RT}=\frac{(1.00\:atm)(0.0350\:L)}{(0.08206\frac{L \cdot atm}{mol \cdot K})(350\:K)}=0.00122\,\text{mol }H_2 \nonumber\]

Step 2: Scale enthalpy from reaction to quantity of H₂ produced:

Since 2 mol of H₂ corresponds to +483.6 kJ absorbed:

\[q=\frac{+483.6\,\text{kJ/mol}}{2\,\text{mol }H_2}\left(0.00122\,\text{mol}\right)=0.295\,\text{kJ} \nonumber\]

Since the value is positive, heat is absorbed by the system.

Exercise \(\PageIndex{15}\)*

Consider the following reaction:

\[\ce{2Al (s) + 3Cl2 (g) \rightarrow 2AlCl3 (s)} \quad \Delta H^{\circ}=-1408.4\,\text{kJ/mol} \nonumber\]

How many grams of Al(s) would have to react to release 325 kJ of energy?

Answer

Since 2 mol of Al corresponds to 1408.4 kJ released and the molar weight of Al is 26.98 g/mol:

\[\left(\frac{2\,\text{mol Al}}{-1408.4\,\text{kJ/mol}}\right)(-325\,\text{kJ})(26.98\,\text{g/mol})=12.5\,g\nonumber\]

Calorimetry

Exercise \(\PageIndex{16}\)*

How much heat is required to heat a 28.4 g ice cube from −23.0 °C to −1.0 °C? The specific heat capacity of ice is 2.05 J/(g⋅K).

Answer

\[q=mc \Delta T=(28.4\:g)\left(2.05\frac{J}{g \cdot K}\right)(-1.0\:°C -(-23.0\:°C))=1281\,\text{ J} = 1.28\,\text{ kJ}\nonumber\]

Note: The temperature change (ΔT) is the same in Celsius and Kelvin.

  \(\Delta T = -1.0\:°C -(-23.0\:°C) = 22.0\:°C \quad\text{and   } \Delta T=272\:K - 250\:K = 22\:K\)

Exercise \(\PageIndex{17}\)**

Using the data below, how much heat (q) is needed to raise the temperature of a 2.50 g piece of copper wire from 20.0 °C to 80.0 °C? How much heat is needed to increase the temperature of an equivalent mass of aluminum by the same amount?

Specific heat capacities:

Cu: c = 0.386 J/(g⋅K)

Al: c = 0.900 J/(g⋅K)

Answer

For Cu: q = 57.9 J

For Al: q = 135 J

Solution

ΔT = T_f - T_i = 80.0 °C - 20.0 °C = 60.0 °C = 60.0 K

q = cmΔT

For Cu: q = 0.386 J/(g⋅K) (2.50 g)(60.0 K) = 57.9 J

For Al: q = 0.900 J/(g⋅K) (2.50 g)(60.0 K) = 135 J

Since the mass and temperature change are the same in both cases, the difference in heat required is due to the specific heat capacity of each metal.  Aluminum has a higher specific heat capacity, so it requires more heat to raise its temperature by the same amount.

Exercise \(\PageIndex{18}\)**

Ethylene glycol, used as a coolant in automotive engines, has a specific heat capacity of 2.42 J⋅g^-1⋅K^-1. A 3.65 x 10³ g sample of ethylene glycol releases 265 kJ of heat.  If the initial temperature was 114.0 °C, what is the final temperature of the ethylene glycol?

Answer

\[q=mc \Delta T=-265\:kJ\left(\frac{1000\:J}{kJ}\right) =-265000\:J= (3.65\,\times 10^3\:g)\left(2.42\frac{J}{g \cdot K}\right)(T_f -114.0°C) \\ T_f=84.0°C\nonumber\]

Note: The final temperature must be lower than the initial temperature because heat is lost from the system. This is consistent with the negative value of q.

Exercise \(\PageIndex{19}\)**

A 360.0-g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 mL of water at 24.0 °C. The final temperature of the water is 42.7 °C. Calculate the initial temperature of the piece of rebar. 

Assume the specific heat of steel is approximately the same as that for iron (0.449 J/(g⋅°C)), and that all heat transfer occurs between the rebar and the water (there is no heat exchange with the surroundings).  Water has a specific heat capacity of 4.18 J/(g⋅°C) and a density of 1.00 g/mL.

Answer

The temperature of the water increases from 24.0 °C to 42.7 °C, so the water absorbs heat. That heat came from the piece of rebar, which cooled, so it must have started at a higher temperature. 

Assuming no heat is lost to the surroundings, all of the heat gained by the water came from the rebar:

\[q_{\text {rebar }}=-q_{\text {water }} \nonumber \]

Using the heat equation q = cmΔT, we can write:

\[c_{\text {rebar }} \times m_{\text {rebar }} \times\left(T_{ f , \text { rebar }}-T_{ i , \text { rebar }}\right)=-c_{\text {water }} \times m_{\text {water }} \times\left(T_{ f \text {,water }}-T_{ i , \text { water }}\right) \nonumber \]

The density of water is 1.00 g/mL, so 425 mL of water = 425 g. Noting that the final temperature of both the rebar and water is 42.7 °C, substituting known values yields:

\[\left(0.449 \frac {J}{g \cdot { }^{\circ} C} \right)(360.0 \: g )\left(42.7 \: { }^{\circ} C -T_{ i , \text { rebar }}\right)=-\left(4.184 \frac {J}{g \cdot { }^{\circ} C} \right)(425 \: g )\left(42.7 \: { }^{\circ} C -24.0 \: { }^{\circ} C \right) \nonumber \]

\[T_{i, \text { rebar }}=\frac{\left(4.184 \frac {J}{g \cdot { }^{\circ} C} \right)(425 \: g )\left(42.7 \: { }^{\circ} C -24.0 \: {}^{\circ} C \right)}{\left(0.449 \frac {J}{g \cdot { }^{\circ} C} \right)(360.0 \: g )}+42.7 \: { }^{\circ} C \nonumber \]

Solving this gives \(T_{i, \text { rebar }}= 248 \: { }^{\circ} C \) , so the initial temperature of the rebar was 248 °C.

Exercise \(\PageIndex{20}\)**

A 248-g piece of copper at 314 °C is dropped into 390 mL of water at 22.6 °C. Assuming that all heat transfer occurs between the copper and the water, calculate the final temperature of the system.  

The specific heat of copper is 0.385 J/(g⋅°C). Water has a specific heat capacity of 4.18 J/(g⋅°C) and a density of 1.00 g/mL.

Answer

\[q_{\text {Cu }}=-q_{\text {water }} \nonumber \]

\[c_{\text {Cu}} \times m_{\text {Cu}} \times\left(T_{ f , \text {Cu}}-T_{ i , \text {Cu}}\right)=-c_{\text {water }} \times m_{\text {water }} \times\left(T_{ f \text {,water }}-T_{ i , \text { water }}\right) \nonumber \]

The density of water is 1.00 g/mL, so 390 mL of water = 390 g. Noting that the final temperature of both the copper and water is same, T_f, substituting known values yields:

\[\left(0.385 \frac {J}{g \cdot { }^{\circ} C}\right)(248\:g )\left(T_f -314\:{}^{\circ} C \right)=-\left(4.18 \frac {J}{g \cdot { }^{\circ} C} \right)(390 \: g )\left(T_f-22.6\:{}^{\circ} C \right) \nonumber \]

\[(95.48 \frac {J}{{ }^{\circ} C})T_f-29981\:J = -1630\frac {J}{{ }^{\circ} C}T_f+36843\:J \\ T_f=38.7\:{}^{\circ} C \nonumber\]

Exercise \(\PageIndex{21}\)**

A 145-g piece of unknown metal is heated to 305.0 °C and then dropped into 275 mL of water at 21.0 °C. The final temperature of the metal and water is 38.0 °C.

Assuming no heat is lost to the surroundings, calculate the specific heat capacity of the metal.

Water has a specific heat capacity of 4.18 J/(g⋅°C) and a density of 1.00 g/mL.

Answer

\[q_{\text {metal }}=-q_{\text {water }} \nonumber \] \[c_{\text {metal}} \times m_{\text {metal}} \times\left(T_{ f , \text {metal}}-T_{ i , \text {metal}}\right)=-c_{\text {water }} \times m_{\text {water }} \times\left(T_{ f \text {,water }}-T_{ i , \text { water }}\right) \nonumber \]

The density of water is 1.00 g/mL, so 275 mL of water = 275 g.

\[c(145\:g )\left(38.0\:°C -305.0\:°C\right)=-\left(4.18 \frac {J}{g \cdot { }^{\circ} C} \right)(275 \: g)\left(38.0\:°C-21.0\:°C\right) \nonumber \] \[c(-38715\:g \cdot °C) = -19541.5\:J\\ c=0.505 \frac {J}{g \cdot { }^{\circ} C} \nonumber\]

Exercise \(\PageIndex{22}\)**

Dissolving 3.0 g of CaCl₂(s) in 150.0 g of water in a coffee cup calorimeter at 22.4 °C causes the temperature of the solution to rise to 25.8 °C. 

What is ΔH (in kJ/mol) for the dissolution of CaCl₂ in water? Is this an exothermic or endothermic process?

Assume that the calorimeter absorbs a negligible amount of heat and that the specific heat of the solution is the same as the specific heat of pure water (4.184 J/(g°C).

Answer

q_dissolving = - q_solution

Step 1: Determine amount of heat released to solution: \[q_{\text{solution}} = cm \Delta T = 4.184 \frac {J}{g \cdot { }^{\circ} C} (150.0\:g + 3.0\:g)(25.8\:°C-22.4\:°C) = 2177\:J = 2.18\:kJ \nonumber\]

Step 2: Determine the moles of CaCl₂ that dissolve:

\[mol_{CaCl_2} = 3.0\:g \left(\frac{mol}{110.98\:g}\right)=0.027\:mol \nonumber\]

Step 3: Find ΔH by dividing by the moles of CaCl₂:

\[q_{\text{dissolving}}=-q_{\text{solution}}=-2.18\:kJ \\ \Delta H = \frac{-2.18\:kJ}{0.027\:mol}=-81\: kJ/mol \nonumber\]

The process is exothermic, because heat is released when CaCl₂ dissolves, causing the temperature of the solution to increase.

Exercise \(\PageIndex{23}\)***

When 100 mL of 0.200 M NaCl(aq) and 100 mL of 0.200 M AgNO₃(aq), both at 21.9 °C, are mixed in a coffee cup calorimeter, the temperature increases to 23.5 °C as solid AgCl forms. 

What is ΔH (in kJ/mol) for the precipitation reaction?

\[\ce{NaCl (aq) + AgNO3 (aq) \rightarrow NaNO3 (aq) + AgCl (s)}\nonumber\]

Assume that the calorimeter absorbs a negligible amount of heat and that the specific heat of the solution is the same as the specific heat of pure water (4.184 J/(g⋅°C)).  The density of the solution can be assumed to be 1.00 g/mL.

Answer

q_rxn = - q_solution

Step 1: Determine the amount of heat released to the solution.  Note that the total volume is 100 mL + 100 mL = 200 mL and the density is 1.00 g/mL.

\[q_{\text{solution}} = cm \Delta T = 4.184 \frac {J}{g \cdot { }^{\circ} C} (200\:g)(23.5\:°C-21.9\:°C) = 1339\:J = 1.34\:kJ \nonumber\]

Step 2: Determine the moles of the limiting reactant:

In this case, NaCl and AgNO₃ react 1:1 and there are equal quantities of both.

\[mol_{NaCl} = 0.200 \left(\frac{mol}{L}\right)(0.100\:L)=0.0200\:mol \nonumber\]

Step 3: Find ΔH by dividing by the moles that react:

\[q_{\text{rxn}}=-q_{\text{solution}}=-1.34\:kJ \\ \Delta H = \frac{-1.34\:kJ}{0.0200\:mol}=-67.0\:kJ/mol \nonumber\]

Exercise \(\PageIndex{24}\)**

When a 0.740-g sample of trinitrotoluene (TNT, molar mass: 213.13 g/mol), is combusted in a bomb calorimeter at constant volume, the temperature of the calorimeter rises from 23.4 °C to 26.9 °C. The total heat capacity of the calorimeter, including the water it contains, is 3358 J/°C.

What is the change in internal energy (ΔE) for the combustion of TNT, in kJ/mol?

Answer

\[q_{rxn}=-q_{calorimeter} \\ q_{calorimeter} = C \Delta T = 3358 \frac {J}{{ }^{\circ} C} (26.9\:°C-23.4\:°C)=11753\:J=11.75\:kJ \\ mol_{TNT}=0.74\:g\left(\frac{mol}{213.13\:g}\right)=0.00347\:mol \\ \Delta E = \frac{-11.75\:kJ}{0.00347\:mol}=-3390\:kJ/mol \nonumber\]

Exercise \(\PageIndex{25}\)**

When 13.6 g of sucrose (molar mass: 342.3 g/mol) is burned in a bomb calorimeter, the temperature increases by 5.6°C. The heat capacity of the calorimeter is calculated at 3.40 kJ/°C. What is the change in internal energy (ΔE) for the combustion of sucrose, in kJ/mol?

Answer

\[q_{rxn}=-q_{calorimeter} \\ q_{calorimeter} = C \Delta T = 3.40 \frac {kJ}{{ }^{\circ} C} (5.6\:°C)=19\:kJ \\ mol_{sucrose}=13.6\:g\left(\frac{mol}{342.3\:g}\right)=0.0397\:mol \\ \Delta E = \frac{-19\:kJ}{0.0397\:mol}=-480\:kJ/mol \nonumber\]

Exercise \(\PageIndex{26}\)***

In a coffee cup calorimeter, 0.100 g of magnesium metal is added to 100.0 mL of 1.00 M HCl at 22.0 °C. The reaction that occurs is:

\[\ce{Mg(s) + 2HCl(aq) \rightarrow MgCl2 (aq) + H2 (g)} \nonumber\]

The temperature of the solution rises to 27.5 °C.

Assume:

    The specific heat capacity of the solution is 4.18 J/(g·°C)

    The density of the solution is 1.00 g/mL

    The calorimeter does not absorb a significant amount of heat

a. Identify the limiting reactant.
b. Calculate the amount of heat released by the reaction (in kJ).
c. Determine the enthalpy change (ΔH, in kJ/mol).

Answer

a. Find moles of each reactant:

\[0.100\,\text{g}\left(\frac{\text{mol}}{24.30\,\text{g}}\right)=0.00412\,\text{mol Mg} \\ 1.00 \frac{\text{mol}}{\text{L}}\left(0.100\,\text{L}\right)=0.100\,\text{mol HCl} \nonumber\]

From the balanced equation, 2 mol HCl reacts with 1 mol Mg.
We need 0.00824 mol HCl to react with all the Mg, and we have 0.100 mol → excess HCl.  Mg is the limiting reactant.

b. Total mass of solution = 100 g (from HCl solution) + 0.1 g Mg = 100.1 g.

\[q_{rxn} = -q_{\text{solution}} = -cm \Delta T = 4.18 \frac {J}{g \cdot { }^{\circ} C} (100.1\:g)(27.5\:°C-22.0\:°C) = -2301\:J = -2.30\:kJ \nonumber\]

c. \[\Delta H = \frac{-2.30\:kJ}{0.00412\:mol}=-558\:kJ/mol\nonumber\]

Hess's Law

---

Exercise \(\PageIndex{27}\)**

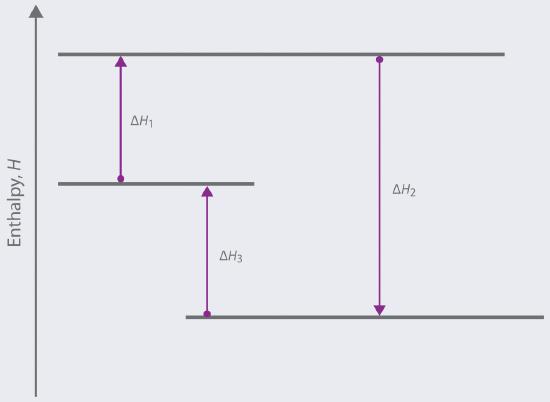
Based on the following energy diagram,

a. write an equation showing how the value of ΔH₂ could be determined if the values of ΔH₁ and ΔH₃ are known.

b. identify each step as being exothermic or endothermic.

Answer

a. ΔH₂ = (-ΔH₁) + (-ΔH₃)

This follows from Hess’s Law, which states that the total enthalpy change for a reaction is the sum of the enthalpy changes for the steps that lead to it. The two steps constituting reaction 2 here are the reverse of reaction 1 and the reverse of reaction 3.

b.  ΔH₁ is endothermic, because the arrow points upward, indicating that enthalpy increases from reactants to products.

    Therefore, −ΔH₁ is exothermic (the reverse of an endothermic process).

    ΔH₃ is also endothermic (arrow points upward), so −ΔH₃ is exothermic as well.

So overall, ΔH₂ is the sum of two exothermic steps, and is exothermic.

Exercise \(\PageIndex{28}\)**

The following sequence of reactions occurs to produce aqueous nitric acid:

\[\ce{4NH3 (g) + 5O2 (g) \rightarrow 4NO (g) + 6H2O (l)}\quad \Delta H = -907\,\text{kJ/mol}\nonumber\]

\[\ce{2NO (g) + O2 (g) \rightarrow 2NO2 (g)}\quad \Delta H = -113\,\text{kJ/mol}\nonumber\]

\[\ce{3NO2 (g) + H2O (l) \rightarrow 2HNO3 (aq) + NO(g)}\quad \Delta H = -139\,\text{kJ/mol}\nonumber\]

The overall reaction is:
\[\ce{4NH3 (g) + 6O2 (g) + NO2 (g) \rightarrow 2HNO3 (aq) + 3NO(g) + 5H2O (l)}\quad \Delta H = ?\nonumber\]

a. What is the ΔH for the reaction as written?

b. How much heat is released when 2.75 mol of HNO₃ is produced?

Answer

a. The sum of three steps give the overall reaction, so their ΔH values should also be added up:

ΔH = -907 kJ/mol + (-113 kJ/mol) + (-139 kJ/mol) = -1159 kJ/mol

b. 1159 kJ is released when 2 mol of HNO₃ is produced (based on the balanced equation), so:

\[q=\left(\frac{-1159\:kJ}{2\:mol}\right)(2.75\:mol)=-1594\:kJ\nonumber\]

1594 kJ of heat is released.

Exercise \(\PageIndex{29}\)**

Calculate ΔH for the process:

\[\ce{Hg2Cl2 (s)  \rightarrow 2Hg (l) + Cl2 (g) }\quad \Delta H = ?\nonumber\]

Given:

\[\ce{Hg (l) + Cl2 (g) \rightarrow HgCl2 (s) }\quad \Delta H = -224\:\text{kJ/mol}\nonumber\]

\[\ce{Hg (l) + HgCl2 (s) \rightarrow Hg2Cl2 (s) }\quad \Delta H = -41.2\:\text{kJ/mol}\nonumber\]

 

Answer

Reverse the first reaction:
\[\ce{HgCl2 (s)\rightarrow Hg (l) + Cl2 (g)  }\quad \Delta H = -(-224\:\text{kJ/mol})\nonumber\]
Reverse the second reaction:
\[\ce{Hg2Cl2 (s) \rightarrow Hg (l) + HgCl2 (s) }\quad \Delta H = -(-41.2\:\text{kJ/mol})\nonumber\]

Summing these modified reactions gives the desired reaction, so

ΔH = 224 kJ/mol + 41.2 kJ/mol = 265 kJ/mol

Exercise \(\PageIndex{30}\)**

Calculate ΔH for the formation of acetylene (C₂H₂) from its elements:

\[\ce{2C (s) + H2 (g)  \rightarrow C2H2 (g) }\quad \Delta H = ?\nonumber\]

Given:

\[\ce{C (s) + O2 (g) \rightarrow CO2 (g) }\quad \Delta H = -393.5\,\text{kJ/mol}\nonumber\]

\[\ce{H2 (g) + 1/2 O2 (g) \rightarrow H2O (l) }\quad \Delta H = -285.8\,\text{kJ/mol}\nonumber\]

\[\ce{2C2H2 (g) + 5 O2 (g) \rightarrow 4 CO2 (g) + 2H2O (l) }\quad \Delta H = -2599.6\,\text{kJ/mol}\nonumber\]

Answer

1. Reverse and halve the third reaction to match the formation of 1 mol C₂H₂ as a product:

\[\ce{2 CO2 (g) + H2O (l) \rightarrow C2H2 (g) + 5/2 O2 (g) }\quad \Delta H = -\frac{1}{2}(-2599.6)=+1299.8\,\text{kJ/mol}\nonumber\]

2. Multiply the first reaction by 2 to cancel out the 2 mol CO₂:

\[\ce{2C (s) + 2O2 (g) \rightarrow 2CO2 (g) }\quad \Delta H = 2(-393.5)=-787\,\text{kJ/mol}\nonumber\]

3. Adding these adjusted reactions and the second reaction as given:

\[\begin{align*}
  \ce{\cancel{2 CO2 (g)} + \cancel{H2O (l)}}  & \ce{\rightarrow C2H2 (g) + \bcancel{5/2 O2 (g)} }\quad &\Delta H = -\frac{1}{2}(-2599.6)=+1299.8\,\text{kJ/mol} \\[2pt]
  \ce{2C (s) + \bcancel{2O2 (g)}} & \ce{\rightarrow \cancel{2CO2 (g)} }\quad &\Delta H = 2(-393.5)=-787\,\text{kJ/mol} \\[2pt]
  \ce{H2 (g) + \bcancel{1/2 O2 (g)}} & \ce{ \rightarrow \cancel{H2O (l) }}\quad &\Delta H = -285.8\,\text{kJ/mol} \\[2pt]
\hline
\\ \ce{2C (s) + H2 (g)} & \ce{  \rightarrow C2H2 (g) }\quad &\Delta H =+227\,\text{kJ/mol}
\end{align*} \nonumber \]

Enthalpies of Formation

Exercise \(\PageIndex{31}\)*

Write a balanced equation corresponding to the standard enthalpy of formation for each compound.

a. C₂H₅OH(l)

b. CaCO₃(s)

c. N₂O₅(g)

Answer

a. \[\ce{2C(s) +3H2 (g) + 1/2 O2 (g) \rightarrow C2H5OH(l)}\nonumber\]

b. \[\ce{Ca(s) +C (s) + 3/2 O2 (g) \rightarrow CaCO3 (s)}\nonumber\]

c. \[\ce{N2 (g) + 5/2 O2 (g) \rightarrow N2O5 (g)}\nonumber\]

Exercise \(\PageIndex{32}\)**

Using data from the reference table, determine ΔH^o_rxn for each chemical reaction.

a.  \[\ce{2Na(s) +Pb(NO3)2 (aq)  \rightarrow 2NaNO3 (aq) + Pb(s)}\nonumber\]

b.  \[\ce{Na2CO3 (s) +H2SO4 (l) \rightarrow Na2SO4 (s) + CO2 (g) + H2O (l)}\nonumber\]

c.  \[\ce{2KClO3 (s) \rightarrow 2KCl (s) + 3 O2(g)}\nonumber\]

Answer

\[ \Delta H_{rxn}^{o} = \sum m\Delta H_{f}^{o}\left ( products \right ) - \sum n\Delta H_{f}^{o}\left ( reactants \right ) \nonumber \]
a. \[ \Delta H_{rxn}^{o} = [(2(-447.5\,\text{kJ/mol}) + 0]-[0 + (-416.3\,\text{kJ/mol})] =-478.7\,\text{kJ/mol}\nonumber \]

b.  \[ \Delta H_{rxn}^{o} = [-1387.1\,\text{kJ/mol} -393.5\,\text{kJ/mol}-285.8\,\text{kJ/mol}]-[-1130.7\,\text{kJ/mol} -909.3\,\text{kJ/mol}] =-26.4\,\text{kJ/mol}\nonumber \]

c.   \[ \Delta H_{rxn}^{o} = [(2(-436.5\,\text{kJ/mol}) + 0]-[2(-397.7\,\text{kJ/mol})] =-77.6\,\text{kJ/mol}\nonumber \]

Exercise \(\PageIndex{33}\)**

Consider the combustion reaction of toluene (C₇H₈) and the associated standard enthalpy change:

\[\ce{C7H8 (l) + 9O2 (g) \rightarrow 7CO2 (g) + 4H2O (l)}\quad \Delta H^\circ = -3910\,\text{kJ/mol}\nonumber\]

Given that the standard enthalpy of formation is -393.5 kJ/mol for CO₂(g) and -285.8 kJ/mol for H₂O(l), find the enthalpy of formation of C₇H₈(l).

Answer

\[\begin{align*} \Delta H_{rxn}^{o} &= \sum m\Delta H_{f}^{o}\left ( products \right ) - \sum n\Delta H_{f}^{o}\left ( reactants \right )=-3910\,\text{kJ/mol} \\ &=[7\Delta H_{f}(CO_2)+ 4\Delta H_{f}(H_2O)]-[\Delta H_{f}(C_7H_8)+9\Delta H_{f}(O_2)]=-3910\,\text{kJ/mol} \\&=[7(-393.5\,\text{kJ/mol})+4(-285.8\,\text{kJ/mol})] -[\Delta H_{f}(C_7H_8)+0]=-3910\,\text{kJ/mol}\end{align*} \\\Delta H_{f}(C_7H_8) = 12.3\,\text{kJ/mol}   \nonumber \]

Bond Energies

Exercise \(\PageIndex{34}\)*

Using the bond energies in Table 5.8.1, determine the approximate enthalpy change for each of the following reactions:

a. \(\ce{H2}(g)+\ce{Br2}(g)⟶\ce{2HBr}(g)\)

b. \(\ce{CH4}(g)+\ce{I2}(g)⟶\ce{CH3I}(g)+\ce{HI}(g)\)

Answer

a. \[\begin{align*}
\Delta H & \approx  \sum D_{\text{bonds broken}} - \sum D_{\text{bonds formed}} \\[4pt]
& \approx\left[ D_{\ce{H-H}} + D_{\ce{Br-Br}} \right] - 2 D_{\ce{H-Br}} \\[4pt]
& \approx[436\,\text{kJ/mol}+190\,\text{kJ/mol}]- 2(370\,\text{kJ/mol}) \\[4pt] &\approx -114\,\text{kJ/mol}
\end{align*} \]

b. \[\begin{align*}
\Delta H & \approx  \sum D_{\text{bonds broken}} - \sum D_{\text{bonds formed}} \\[4pt]
& \approx\left[ D_{\ce{C-H}} + D_{\ce{I-I}} \right] - [D_{\ce{H-I}}+D_{\ce{C-I}}] \\[4pt]
& \approx[415\,\text{kJ/mol}+150\,\text{kJ/mol}]- [295\,\text{kJ/mol}+240\,\text{kJ/mol}] \\[4pt] &\approx 30\,\text{kJ/mol}
\end{align*} \]

Exercise \(\PageIndex{35}\)***

How does the bond energy of HCl differ from the standard enthalpy of formation of HCl(g)?

Answer

The bond energy of HCl is the energy required to break one mole of H–Cl bonds in the gas phase into individual atoms. This is always a positive value because breaking bonds requires energy:

\[\ce{HCl(g) -> H(g) + Cl(g)} \nonumber \]

The standard enthalpy of formation of HCl(g) is the enthalpy change when one mole of HCl(g) forms from hydrogen and chlorine in their standard states, diatomic gases:

\[\ce{1/2 H2(g) + 1/2 Cl2(g) -> HCl(g)} \nonumber \]

This process involves breaking the H–H and Cl–Cl bonds and forming H–Cl bonds. The enthalpy of formation reflects the net energy change, and may be positive or negative depending on the relative strengths of the bonds broken and formed. For HCl(g), the process is exothermic, so \(\Delta H_f^\circ\) is negative.

In summary:

• Bond energy describes the energy required to break a specific bond (H–Cl) in isolation.
• Enthalpy of formation accounts for the overall energy change in forming a compound from elements in their standard states, involving bonds forming and breaking.

Additional Problems

Exercise \(\PageIndex{36}\)***

In a coffee cup calorimeter, 50.0 mL of 1.00 M HCl is mixed with 75.0 mL of 0.80 M NaOH, both at 22.6 °C. The temperature of the resulting solution rises to 27.7 °C. The calorimeter itself has a heat capacity of 41.8 J/°C.

\[\ce{NaOH(aq) + HCl(aq) \rightarrow NaCl(aq) + H2O (l)} \nonumber\]

Assume:

• Specific heat capacity of the solution is 4.18 J/(g·°C)
• Density of the solution is 1.00 g/mL
• All of the heat from the reaction is transferred to the calorimeter and solution.

a. Calculate the total amount of heat released by the reaction (in kJ), including the heat absorbed by the calorimeter.

b. Determine the enthalpy change (in kJ/mol).

c. Is this reaction exothermic or endothermic?

Answer

Volume of solution = 50.0 mL + 75.0 mL = 125.0 mL.  Since density is 1.00 g/mL, mass of solution is 125.0 g.

a. \[-q_{rxn} = q_{\text{solution}}+q_{calorimeter} = cm \Delta T + C\Delta T= 4.18 \frac {J}{g \cdot { }^{\circ} C} (125.0\:g)(27.7\:°C-22.6\:°C)+ 41.8 \frac {J}{{ }^{\circ} C} (27.7\:°C-22.6\:°C)= 2878\:J \\ q_{rxn}= -2.88\:kJ \nonumber\]

b. Moles of each reactant:

\[1.00 \frac{mol}{L}(0.0500\:L)=0.0500\:mol \\ 0.80\frac{mol}{L}(0.0750\:L)=0.0600\:mol \nonumber\]

From the balanced equation (1:1 ratio), HCl is the limiting reactant.

\[\Delta H = \frac{-2.88\:kJ}{0.0500\:mol}=-57.6\:kJ/mol\nonumber\]

c.  The temperature of the solution increased, so heat was released to the surroundings. The reaction is exothermic.

Exercise \(\PageIndex{37}\)***

A 1.50 g sample of ethanol (C₂H₅OH(l)) is combusted in a bomb calorimeter. The temperature of the calorimeter and its contents rises by 5.17 °C. The total heat capacity of the calorimeter is 9.21 kJ/°C.

The balanced combustion reaction is:
\[\ce{C2H5OH(l) + 3O2(g) ⟶ 2CO2(g) + 3H2O(l)} \nonumber\]

Given:

    ΔH_f^∘[CO₂(g)]=−393.5 kJ/mol

    ΔH_f^∘[H₂O(l)]=−285.8 kJ/mol

a. Calculate the amount of heat released when 1.50 g of ethanol is combusted.
b. Determine the ΔH^∘ (in kJ/mol) for the combustion of ethanol.  Assume   ΔH^∘ ≈ ΔE^∘.
c. What is the standard enthalpy of formation of ethanol, ΔH_f^∘[C₂H₅OH(l)] based on this data?

Answer

a.  \[q_{rxn}=-q_{calorimeter} \\ q_{calorimeter} = C \Delta T = 9.21 \frac {kJ}{{ }^{\circ} C} (5.17\:°C)=47.6\:kJ \\ q_{rxn}=-47.6\:kJ \nonumber\]

b.  \[
\begin{align*}
\text{mol}_{\text{ethanol}} &= 1.50\,\text{g} \left(\frac{\text{mol}}{46.07\,\text{g}}\right) = 0.0326\,\text{mol} \\
\Delta H^\circ &= \frac{-47.6\ \text{kJ}}{0.0326\,\text{mol}} = -1460\ \text{kJ/mol}
\end{align*}
\]

c. \[\begin{align*} \Delta H_{rxn}^{o} &= \sum m\Delta H_{f}^{o}\left ( products \right ) - \sum n\Delta H_{f}^{o}\left ( reactants \right )=-1460\:\text{kJ/mol} \\ &=[2\Delta H_{f}(CO_2)+ 3\Delta H_{f}(H_2O)]-[\Delta H_{f}(C_2H_5OH)+3\Delta H_{f}(O_2)]=-1460\:\text{kJ/mol} \\&=[2(-393.5\:\text{kJ/mol})+3(-285.8\,\text{kJ/mol})] -[\Delta H_{f}(C_2H_5OH)+0]=-1460\:\text{kJ/mol}\end{align*} \\\Delta H_{f}(C_2H_5OH) = -184\:\text{kJ/mol}   \nonumber \]

Exercise \(\PageIndex{38}\)**

Consider the reaction: \(2A(g) \rightarrow A_2(g)\) 

This reaction is carried out in a cylinder with a movable piston at constant external pressure.

a. Is heat absorbed or released during this reaction? What is the sign of q?
b. Does the system do work on the surroundings, or is work done on the system? What is the sign of w?
c. Based on your answers above, what is the sign of the change in internal energy (ΔE)?

Answer

a. The reaction forms a bond, which releases energy. Therefore, heat is released. q is negative.

b.  The system contracts as gas particles combine (fewer moles of gas), so volume decreases, meaning the surroundings do work on the system. w is positive.

c.  ΔE = q + w  

Since q is negative and w is positive, the overall sign of ΔE depends on their relative sizes.  Often, q is larger than w, but we can not be certain without values.

Exercise \(\PageIndex{39}\)***

The standard enthalpies of formation at 298 K are:

    ΔH_f^∘[H(g)]=+218 kJ/mol

    ΔH_f^∘[Cl(g)]=+121 kJ/mol

    ΔH_f^∘[HCl(g)]=−92 kJ/mol

a.  Write a balanced equation corresponding to the standard enthalpy of formation of H(g), Cl(g) and HCl(g).

b. Use Hess’s Law and the equations from part (a) to construct a reaction pathway that represents the dissociation of HCl(g) into its atoms.

c.  Use the given enthalpies of formation to estimate the bond energy of the H–Cl bond.

Answer

a. \[
\begin{align*}
\frac{1}{2}\ce{H2}(g)                &⟶ \ce{H}(g) \\
\frac{1}{2}\ce{Cl2}(g)              &⟶ \ce{Cl}(g) \\
\frac{1}{2}\ce{H2}(g) + \frac{1}{2}\ce{Cl2}(g) &⟶ \ce{HCl}(g)
\end{align*}
\]

b.  The desired reaction is:

\[HCl(g)⟶H(g) + Cl(g) \nonumber\]

Using Hess’s Law, we combine the formation of H(g) and Cl(g) with the reverse of the formation of HCl(g):
    \[
    \dfrac{1}{2}\ce{H2}(g)⟶\ce{H}(g)\hspace{105px} ΔH^\circ_f(H)=218\,\text{kJ/mol}\\\dfrac{1}{2}\ce{Cl2}(g)⟶\ce{Cl}(g)\hspace{99px}ΔH^\circ_f(Cl)=121\,\text{kJ/mol}\\
    \underline{\ce{HCl}(g)⟶\dfrac{1}{2}\ce{H2}(g)+\dfrac{1}{2}\ce{Cl2}(g)\hspace{20px}−ΔH^\circ_f(HCl)=+92 \,\text{kJ/mol}}\\
    \ce{HCl}(g)⟶\ce{H}(g)+\ce{Cl}(g)\hspace{58px}\nonumber\]

c.  The bond energy of H–Cl is equal to the enthalpy change for breaking the bond:

\(\begin{align*} D_\ce{HCl}=-ΔH^\circ&=ΔH^\circ_{f}(H)+ΔH^\circ_{f}(Cl)-ΔH^\circ_{f}(HCl)\\
    &=218\,\text{kJ/mol}+121\,\text{kJ/mol}-(-92\,\text{kJ/mol}) \\
    &=431\,\text{kJ/mol}
    \end{align*}\)