5.4: Calorimetry

Learning Objectives

• Explain how calorimetry demonstrates the law of conservation of energy.
• Describe the relationship between heat (\(q\)), temperature change (\(\Delta T\)), and heat capacity (\(C\), specific and molar).
• Analyze calorimetry data to calculate heat transferred (\(q\)), temperature change (\(\Delta T\)), heat capacity (\(C\)), and the change in enthalpy (\(\Delta H\)) or internal energy (\(\Delta E\)).

Thermal energy cannot be measured directly, but the temperature change caused by heat transfer can be. Calorimetry refers to a set of techniques used to measure energy changes in chemical processes using devices called calorimeters. For these measurements to be meaningful, the temperature change observed must be related to the amount of heat absorbed or released by the system. We begin this section by exploring how heat affects temperature.

Heat Capacity

We’ve seen that the temperature of an object changes when it absorbs or loses thermal energy. The temperature change depends on both the amount of heat transferred (\(q\)) and the object’s heat capacity (\(C\)), which is the amount of energy required to raise the temperature of the object by 1 °C. Units are joules per degree Celsius (J/°C):

\[ \text{Heat Capacity (C)}=\frac{q}{\Delta T} \nonumber\]

where q is the amount of heat (in joules), and \(\Delta T\) is \(T_{final} − T_{initial}\). Since the size of one Kelvin is equal to one degree Celsius, \(\Delta T\) is the same whether in K or °C, as long as you don’t mix the units within a single calculation.

The heat capacity of an object depends on both its mass and its composition. For example, doubling the mass of an object doubles its heat capacity. Because of this, heat capacity is often reported per gram or per mole of substance.

The molar heat capacity (\(C_m\)) is the amount of energy needed to increase the temperature of 1 mol of a substance by 1°C; the units of \(C_m\) for molar heat capacity are thus J/(mol °C). We can relate the quantity of a substance in moles (\(n\)), the amount of heat transferred (\(q\)), its molar heat (\(C_m\)), and the temperature change (\(\Delta T\)):

\[q = nC_m \Delta T \label{3.5.2} \]

The specific heat capacity (\(C\)) is the amount of energy needed to increase the temperature of 1 g of a substance by 1°C; its units are thus J/(g°C). We can use the specific heat capacity to relate the mass of a substance (\(m\)), the amount of heat transferred (\(q\)), its specific heat (\(c\)), and the temperature change (\(\Delta T\)):

\[q = mc \Delta T \label{3.5.3} \]

The specific heat capacities of some common substances are given in Table \(\PageIndex{1}\). Most solids have specific heat values below 1 J/(g·°C), and most liquids are around 2 J/(g·°C). Water is a major exception: the specific heat of ice is about twice that of most solids, and the specific heat of liquid water (4.18 J/(g·°C)) is among the highest known.

Table \(\PageIndex{1}\): Specific Heats of Selected Substances at 25°C

Compound	Specific Heat [J/(g°C)]	Compound	Specific Heat [J/(g°C)]
H2O (s) (-10^oC)	2.05	Al(s)	0.897
H2O (l)	4.18	Fe(s)	0.449
H2O (g)	2.062	Cu(s)	0.385
CH3OH (methanol)	2.531	Au(s)	0.129
CH3CH2OH (ethanol)	2.438	Hg(l)	0.140
n-C6H14 (n-hexane)	2.270	NaCl(s)	0.864
C6H6 (benzene)	1.741	MgO(s)	0.918
C(s) (graphite)	0.709	SiO2(s) (quartz)	0.742
C(s) (diamond)	0.509	CaCO3(s) (calcite)	0.915

Water’s unusually high specific heat has important implications for life on Earth. For a 1 °C temperature change, a given mass of water stores or releases more than five times as much heat as the same mass of granite or limestone. This is why coastal regions have milder climates than inland areas: the ocean absorbs heat in summer and releases it slowly in winter. It’s also why swimming pools and waterbeds are heated - large amounts of energy are needed to raise and maintain a comfortable temperature. Because the human body is approximately 70% water by mass, it resists temperature change. This helps regulate our internal body temperature without requiring overly fine control.

Example \(\PageIndex{1}\): Solar Heating

A home solar energy storage unit uses 400 L of water for storing thermal energy. On a sunny day, the initial temperature of the water is 22.0 °C. During the day, the water temperature rises to 38.0 °C as it circulates through the water wall. How much energy has been stored in the water? The density of water at 22.0 °C is 0.998 g/mL, and specific heat capacity is 4.18 J/(g°C).

Passive solar system. During the day (a), sunlight is absorbed by water circulating in the water wall. At night (b), heat stored in the water wall continues to warm the air inside the house.

Given: volume and density of water and initial and final temperatures

Asked for: amount of energy stored

Strategy:

1. Use the density of water at 22.0 °C to obtain the mass of water that corresponds to 400 L of water. Then compute \(ΔT\) for the water.
2. Determine the amount of heat absorbed by substituting values for mass, specific heat capacity, and ΔT into Equation \(\ref{3.5.3}\).

Solution:

A The mass of water is

\[ \begin{align*} \text{mass of } \ce{H2O} &= 400 \; \cancel{L}\left ( \dfrac{1000 \; \cancel{mL}}{1 \; \cancel{L}} \right ) \left ( \dfrac{0.998 \; g}{1 \; \cancel{mL}} \right ) \\[4pt] &= 3.99\times 10^{5}g\; \ce{H2O} \end{align*} \nonumber \]

The temperature change (\(ΔT\)) is

\[38.0 ^oC − 22.0 ^oC = +16.0^oC. \nonumber \]

B From Table \(\PageIndex{1}\), the specific heat of water is 4.18 J/(g°C). From Equation \(\ref{3.5.3}\), the heat absorbed by the water is thus

\[ \begin{align*} q &=mc \Delta T \\[4pt] &= \left ( 3.99 \times 10^{5} \; \cancel{g} \right )\left ( \dfrac{4.18 \; J}{\cancel{g}\cdot \cancel{^{o}C}} \right ) \left ( 16.0 \; \cancel{^{o}C} \right ) \\[4pt] &= 2.67 \times 10^{7}\,J = 2.67 \times 10^{4}\,kJ \end{align*} \nonumber \]

Both \(q\) and \(ΔT\) are positive, consistent with the water absorbing energy.

Exercise \(\PageIndex{1}\): Solar Heating

Some solar heating systems circulate air over a bed of rocks to absorb thermal energy from the sun. If a house uses a system with 2500 kg of sandstone rocks, what amount of energy is stored if their temperature increases from 20.0 °C to 34.5 °C during the day? Assume the specific heat of sandstone is approximately the same as that of quartz (\(\ce{SiO2}\), 0.742 J/(g·°C).

Answer

\[ \begin{align*} q &=mc \Delta T \\[4pt] &= \left ( 2500 \; \cancel{kg} \right ) \left(\frac{1000\cancel{g}}{\cancel{kg}}\right)\left ( \dfrac{0.742  \; J}{\cancel{g}\cdot \cancel{^{o}C}} \right ) \left ((34.5-20.0) \; \cancel{^{o}C} \right ) \\[4pt] &= 2.68 \times 10^{7}\,J = 2.68 \times 10^{4}\,kJ \end{align*} \nonumber \]

Even though the mass of sandstone is more than six times the mass of the water in Example \(\PageIndex{1}\), the thermal energy stored is nearly the same due to water’s much higher specific heat capacity.

Principle of Calorimetry

When two objects at different temperatures are placed in contact, heat flows from the warmer object to the cooler one until both reach the same final temperature. According to the law of conservation of energy, the total energy remains constant during this process:

\[q_{cold} + q_{hot} = 0 \label{3.5.4} \]

This means that the amount of heat lost by the warmer object is equal to the amount of heat gained by the cooler object. Because heat flows in opposite directions for each, the signs of their q values are also opposite:

\[q_{cold} = −q_{hot} \label{3.5.5} \]

We can use this relationship to calculate the final temperature when two substances at different initial temperatures are brought into contact, as long as we know their mass and specific heat capacity.

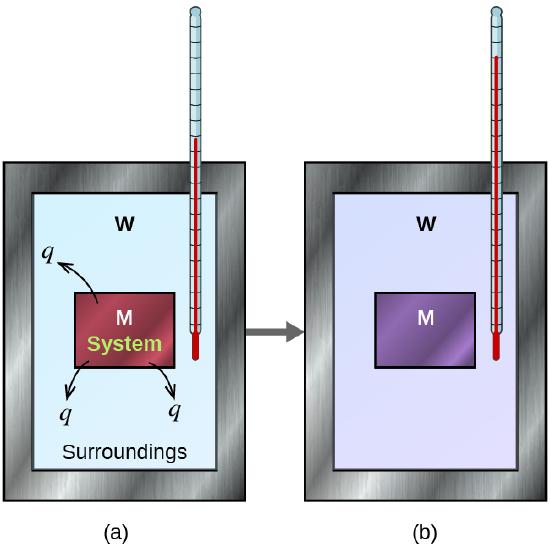
For example, if a hot metal block is placed into cool water, heat flows from the metal to the water (Figure \(\PageIndex{1}\)). The heat lost by the metal equals the heat gained by the water. This principle is used in calorimetry to determine unknown temperatures, specific heats, or other thermal properties. A calorimeter is a thermally insulated container that limits heat exchanged between its contents and the wider surroundings to facilitate calorimetry experiments. Calorimeters will have their own heat capacities that need to be measured, however these are often negligible in comparison to their contents and can sometimes be ignored in calculations.

 

Figure \(\PageIndex{1}\): Heat flows from the hot metal (M) to the cooler water (W) in part (a), until they have the same final temperature in part (b). At this point, thermal equilibrium is achieved.

Example \(\PageIndex{2}\): Thermal Equilibration of Copper and Water

If a 30.0 g piece of copper pipe (c = 0.385 J/(g°C)) at 80.0 °C is placed in 100.0 g of water (c = 4.18 J/(g°C)) at 27.0 °C, what is the final temperature? Assume that no heat is transferred to the surroundings.

Given: mass, initial temperature, and specific heat capacity of two objects

Asked for: final temperature

Strategy: The heat lost by the metal must be gained by the water:

\(q_{\text{metal}} = -q_ {\text{water}}\)

The final temperature reached by the metal and water must be the same.

Solution

The heat of the metal and water can be written in terms of the specific heat capacity, mass, and temperature change:

\(\begin{align*} q_{\text{metal}} &= -q_ {\text{water}} \\ c_{\text{metal}}(m_{\text{metal}})(T_f-T_i) &= -c_{\text{water}}(m_{\text{water}})(T_f-T_i) \\ (0.385 \frac{J}{g°C})(30.0g)(T_f-80.0 °C)&=-(4.18 \frac{J}{g°C})(100.0g)(T_f-27.0 °C) \\ 11.55 \frac{J}{°C}T_f - 924J&=-418 \frac{J}{°C}T_f + 11286J \\ 429.55\frac{J}{°C}T_f &=12210 J \\ T_f = 28.4°C\end{align*}\)

It is expected that the water will increase in temperature since the added copper pipe was hotter than the water. However, the temperature increase is small because the water has both a much greater mass (three times more) and a much higher specific heat capacity (over 10 times greater) than copper.

Exercise \(\PageIndex{2}\): Thermal Equilibration of Gold and Water

If a 14.0 g chunk of gold (c= 0.129 J/(g°C)) at 20.0°C is dropped into 25.0 g of water (c = 4.18 J/(g°C)) at 80.0 °C, what is the final temperature if no heat is transferred to the surroundings?

Answer

\(\begin{align*} q_{\text{metal}} &= -q_ {\text{water}} \\ c_{\text{metal}}(m_{\text{metal}})(T_f-T_i) &= -c_{\text{water}}(m_{\text{water}})(T_f-T_i) \\ (0.129 \frac{J}{g°C})(14.0g)(T_f-20.0 °C)&=-(4.18 \frac{J}{g°C})(25.0g)(T_f-80.0 °C) \\ 1.806 \frac{J}{°C}T_f - 36.12J&=-104.5 \frac{J}{°C}T_f + 8360J \\ 106.306\frac{J}{°C}T_f &=8396.12 J \\ T_f = 79.0°C\end{align*}\)

Exercise \(\PageIndex{3}\): Thermal Equilibration of Aluminum and Water

A 28.0 g chunk of aluminum (c = 0.897 J/(g°C)) is dropped into 100.0 g of water (c = 4.18 J/(g°C)) with an initial temperature of 20.0 °C. If the final temperature of the water is 24.0 °C, what was the initial temperature of the aluminum? (Assume that no heat is transferred to the surroundings.)

Answer

\(\begin{align*} q_{\text{metal}} &= -q_ {\text{water}} \\ c_{\text{metal}}(m_{\text{metal}})(T_f-T_i) &= -c_{\text{water}}(m_{\text{water}})(T_f-T_i) \\ (0.897 \frac{J}{g°C})(28.0g)(24.0 °C - T_i)&=-(4.18 \frac{J}{g°C})(100.0g)(24.0°C -20.0 °C) \\ 602.784 J - 25.116 \frac{J}{°C}T_i &=-1672J \\ T_i &= 90.6°C\end{align*}\)

Calorimetry of Chemical Reactions

Reactions carried out in a calorimeter can cause a temperature change in the contents of the calorimeter, which reflect the energy change of the reaction. The purpose of a calorimeter is to isolate the reaction from the wider surroundings so these energy flows can be properly measured using temperature changes. Within the calorimeter, the chemical reaction is the system and the calorimeter and its contents are the surroundings. The amount of heat absorbed or released by the system is equal in magnitude and opposite in sign to the heat exchanged by the surroundings:

\[ q_{system}=-q_{surroundings} \nonumber \]

•   If the reaction releases heat (\(q_{system} < 0\)), the calorimeter absorbs heat (\(q_{surroundings} > 0\)), and its temperature rises.
•   If the reaction absorbs heat (\(q_{system} > 0\)), the calorimeter loses heat (\(q_{surroundings} < 0\)), and its temperature falls.

The heat absorbed or released by the calorimeter (\(q_{surroundings}\)) includes the physical interior of the calorimeter (\(q_{calorimeter}\)) and any solvents (\(q_{solvent}\)) present in solution-based reactions:

\[ q_{surroundings}=q_{calorimeter} + q_{solvent} \nonumber \]

In practical terms, the heat exchanged by the calorimeter is often small compared to the heat exchanged by the solvent (\(q_{solvent} > q_{calorimeter}\)) and so we often assume \(q_{calorimeter}\) is negligible and use the following relationship in calculations:

\(\begin{align*}
q_{system}&=-q_{surroundings}\\[4pt]
q_{system}&=-(q_{calorimeter} + q_{solvent})\\[4pt]
q_{system}&≈-q_{solvent}\\[4pt]
\end{align*}\nonumber \)

With this relationship we can use the heat capacity of the solvent, the amount of solvent present, and the measured change in temperature to calculate how much energy was transferred by the reaction. Be sure to use consistent units for the amount of solvent (mass or moles) with the heat capacity used.

\[ q_{system}≈-n_{solvent}C_{solvent} \Delta T_{solvent} \nonumber \]

Once we know the total heat transferred by a chemical reaction, we can calculate the heat released or absorbed per gram or per mole of reactant, based on the amounts of substances involved.

Constant-Pressure Calorimetry

A constant-pressure calorimeter is one of the simplest types of calorimeters. It usually consists of an insulated container, a thermometer, a stirrer, and a loosely fitting lid. A common example is the coffee-cup calorimeter, shown in Figure \(\PageIndex{2}\).

In this type of calorimeter, the pressure remains constant because the system is open to the atmosphere. This allows us to directly measure the enthalpy change of the reaction (\(\Delta H_{rxn}\)), which is the heat transferred at constant pressure (\(q_p = q_{rxn} = q_{system}\)). As discussed above, the heat released or absorbed by the reaction is equal in magnitude and opposite in sign to the heat absorbed or released by the calorimeter and its contents.

\[ \Delta H_{rxn}=q_{system}=-q_{surroundings}≈-q_{solvent} \label{3.5.8} \]

The use of a constant-pressure calorimeter is illustrated in Example \(\PageIndex{3}\).

Figure \(\PageIndex{2}\): A Coffee-Cup Calorimeter. This simplified version of a constant-pressure calorimeter consists of two Styrofoam cups nested and sealed with an insulated stopper to thermally isolate the system (the solution being studied) from the surroundings (the air and the laboratory bench). Two holes in the stopper allow the use of a thermometer to measure the temperature and a stirrer to mix the reactants.

Example \(\PageIndex{3}\): ΔH for Dissolution of Potassium Hydroxide

When 5.03 g of solid potassium hydroxide is dissolved in 100.0 mL of distilled water in a coffee-cup calorimeter, the temperature of the solution increases from 23.0 °C to 34.7 °C. The density of solution is 0.9969 g/cm³. What is \(ΔH\) (in kilojoules per mole) for the dissolution of KOH in water? Assume that the calorimeter absorbs a negligible amount of heat and, because of the large volume of water, the specific heat capacity of the solution is the same as the specific heat capacity of pure water (4.184 J/(g°C)).

Given: mass of substance, volume of solvent, and initial and final temperatures

Asked for: ΔH

Strategy:

1. Calculate the mass of the solution from its volume and density. Calculate the temperature change of the solution.
2. Find the heat flow that accompanies the dissolution using the specific heat, mass, and temperature change of the solution.
3. Use the molar mass of \(\ce{KOH}\) to calculate \(ΔH\).

Solution:

A To calculate ΔH, we must first determine the amount of heat released in the calorimetry experiment. The mass of the solution is

\[ \left (100.0 \; \cancel{mL}\; \ce{H2O} \right ) \left ( 0.9969 \; g/ \cancel{mL} \right )+ 5.03 \; g \; \ce{KOH}=104.72 \; g \nonumber \]

The temperature change is

\[(34.7\, ^oC − 23.0 \,^oC) = +11.7\, ^oC. \nonumber \]

B We assume that the specific heat of the solution is the same as that of water. The heat flow that accompanies dissolution is thus

\[ \begin{align*} q_{water}&=mc \Delta T \\[4pt] &=\left ( 104.72 \; \cancel{g} \right ) \left ( \dfrac{4.184 \; J}{\cancel{g}\cdot \cancel{^{o}C}} \right )\left ( 11.7 \; \cancel{^{o}C }\right ) \\[4pt] &=5130 \; J = 5.13 \; kJ \end{align*} \nonumber \]

The temperature of the solution increased because heat was absorbed by the solution (\(q > 0\)). Where did this heat come from? It was released by \(\ce{KOH}\) dissolving in water.

\[ΔH_{rxn} = −q_{water} = −5.13\, kJ \nonumber \]

This experiment shows that dissolving 5.03 g of$KOH$ in water releases 5.13 kJ of heat. Because the temperature of the solution increased, the dissolution of \(\ce{KOH}\) in water must be exothermic.

C The last step is to use the molar mass of \(\ce{KOH}\) to calculate \(ΔH_{soln}\), i.e., the heat released when dissolving 1 mol of \(\ce{KOH}\):

\[ \begin{align*} \Delta H_{soln} &= \left ( \dfrac{-5.13 \; kJ}{5.03 \; \cancel{g}} \right )\left ( \dfrac{56.11 \; \cancel{g}}{1 \; mol} \right ) \\[4pt] &=-57.2 \; kJ/mol \end{align*} \nonumber \]

Because energy is an extensive property—it depends on the amount of substance—we typically report enthalpy changes per mole of reactant so the value can be applied to other quantities or used in thermochemical equations.

Exercise \(\PageIndex{4}\): ΔH for Dissolution of Ammonium Bromide

A coffee-cup calorimeter contains 50.0 mL of distilled water at 22.7 °C. Solid ammonium bromide (3.14 g) is added and the solution is stirred, giving a final temperature of 20.3°C. Using the same assumptions as in Example \(\PageIndex{3}\), find \(ΔH\) for the dissolution of \(\ce{NH4Br }\) (in kilojoules per mole).

Answer

\[ \begin{align*} q_{rxn} =  -q_{water}&=-mc \Delta T \\[4pt] &=-\left ( 52.985 \; \cancel{g} \right ) \left ( \dfrac{4.184 \; J}{\cancel{g}\cdot \cancel{^{o}C}} \right )\left (-2.4 \; ^{o}C \right ) \\[4pt] &=532 J  \end{align*} \nonumber \]

\[3.14g \left(\frac{mol}{97.94 g} \right)=0.0321 mol \\ \Delta H = \frac{532J}{0.0321mol}=16594\; J/mol=16.6\;kJ/mol\nonumber\]

 

Example \(\PageIndex{4}\) Heat Produced by an Exothermic Reaction

When 50.0 mL of 1.00 M HCl (aq) and 50.0 mL of 1.00 M NaOH (aq), both at 22.0 °C, are added to a coffee cup calorimeter, the temperature of the mixture reaches a maximum of 28.9 °C. Assume that the calorimeter absorbs a negligible amount of heat and that the specific heat of the solution is the same as the specific heat of pure water (4.184 J/(g°C)). The density of the solution is 1.0 g/mL.

What is ΔH_rxn in kJ/mol?

HCl(aq) + NaOH(aq) ⟶ NaCl(aq) + H₂O(l)

Solution

To visualize what is going on, imagine that you could combine the two solutions so quickly that no reaction took place while they mixed; then after mixing, the reaction took place. Before the reaction begins, the combined solution has a total volume of 100.0 mL and an initial temperature of 22.0 °C. The HCl and NaOH then react until the solution temperature reaches 28.9 °C.

The heat released by the neutralization reaction is absorbed by the solution, raising its temperature. Therefore:

\(q_{reaction} = -q_{solution}\)

(It is important to remember that this relationship only holds if the calorimeter does not absorb any heat from the reaction, and there is no heat exchange between the calorimeter and the outside environment.)

Next, we know that the heat absorbed by the solution depends on its specific heat, mass, and temperature change:

\(q_{solution} = (c×m×ΔT)_{solution}\)

\(q_{solution} = (4.184 J/g °C)(100.0 mL)(1.0 g/mL)(28.9 °C−22.0 °C)=2887 J = 2.9 kJ\)

\(q_{reaction} = -q_{solution}=−2.9 kJ\)

Finally, we divide by the number of moles of reaction that occurred. The balanced equation shows that 1 mol of HCl reacts with 1 mol of NaOH. Since the reactants are present in equal amounts:

\(\text{mol HCl}=\text{mol NaOH}=1.00 \frac{mol}{L}(0.0500L)=0.0500 mol\)

\( \Delta H = \frac{-2.89kJ}{0.0500mol}=-58 kJ/mol\)

This value represents the enthalpy change for the neutralization of one mole of a strong acid with a strong base.

Chemistry in Everyday Life: Thermochemistry of Hand Warmers

On a cold day, you might use a hand warmer to keep your hands warm while working or playing outside. A common reusable hand warmer contains a supersaturated solution of sodium acetate (NaCH₃COO) and a small metal disk. Bending the disk triggers nucleation sites, which cause the sodium acetate to rapidly crystallize from the solution.

The process:

NaCH₃COO(aq) ⟶ NaCH₃COO(s) 

is exothermic. That heat is transferred to your hands, providing warmth (at least temporarily!). When the hand warmer is reheated, the sodium acetate redissolves, and the device can be used again.

Exercise \(\PageIndex{5}\) Heat Flow in an Instant Ice Pack

When solid ammonium nitrate (NH₄NO₃) dissolves in water, the solution becomes cold. This is the principle behind an instant cold pack. 

In a calorimetry experiment, 3.21 g of solid NH₄NO₃ is dissolved in 50.0 g of water at 24.9 °C in a calorimeter. After the salt dissolves, the final temperature of the solution is 20.3 °C.

Assume:

• The calorimeter absorbs a negligible amount of heat.
• The specific heat of the solution is the same as the specific heat of pure water (4.184 J/(g°C)).
• The density of the solution is 1.0 g/mL.

What is \(ΔH\) (in kilojoules per mole) for the dissolution of NH₄NO₃ in water?

An instant cold pack contains ammonium nitrate and water in separate compartments. When the inner pouch is broken, the ammonium nitrate dissolves and absorbs heat, cooling the pack.

Answer

We assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself), therefore:

\[q_{reaction} = -q_{solution} \nonumber\]

\[ \begin{align*} q_{solution}&=mc \Delta T \\[4pt] &=\left (53.21 \; \cancel{g} \right ) \left ( \dfrac{4.184 \; J}{\cancel{g}\cdot \cancel{^{o}C}} \right )\left ( 20.3\; ^{o}C - 24.9 \; ^{o}C \right ) \\[4pt] &=- 1024 \;J = -1.02 \; kJ \end{align*} \nonumber \]

\[q_{reaction} = -q_{solution} = +1.02 kJ \nonumber\]

\[ \begin{align*} \Delta H_{soln} &= \left ( \dfrac{1.02 \; kJ}{3.21 \; \cancel{g}} \right )\left ( \dfrac{80.04 \; \cancel{g}}{1 \; mol} \right ) \\[4pt] &=+25.5 \; kJ/mol \end{align*} \nonumber \]

This positive value confirms that the dissolution of ammonium nitrate is endothermic: it absorbs heat from the surroundings, which causes the cold pack to feel cold.

Constant-Volume Calorimetry

Constant-pressure calorimeters are not well suited for reactions involving gases, such as combustion reactions, because gases often produce large pressure and volume changes that are difficult to contain or measure accurately in an open system. For these, a constant-volume calorimeter, such as a bomb calorimeter, is used (Figure \(\PageIndex{3}\)). 

In a bomb calorimeter, the reactant is placed in a steel cup inside a sealed steel container with a fixed volume (called the “bomb”). The bomb is filled with excess oxygen gas, sealed, and placed inside an insulated container holding a known mass of water.

Because combustion reactions are typically exothermic, they release heat, which raises the temperature of the surrounding water bath and the calorimeter. If the heat capacity of the bomb and the mass of water are known, the heat released by the reaction can be calculated.

Figure \(\PageIndex{3}\): A Bomb Calorimeter. The reaction is triggered by passing an electric current through a wire that ignites the sample. Since the volume is fixed, the heat measured corresponds to the change in internal energy of the reaction, not the enthalpy.

Because the volume of the system is constant (the bomb cannot expand or contract), the pressure changes during the reaction, but no pressure-volume work is done. As a result, the heat released is equal to the change in internal energy (\(\Delta E\)):

\[q_v = \Delta E \nonumber\]

This contrasts with constant-pressure calorimetry, where the heat measured corresponds to (\(\Delta H\)). As discussed earlier, \(\Delta E\) and \(\Delta H\) are often similar, especially when the number of moles of gas doesn’t change much.

Before using a bomb calorimeter to measure unknown heats of combustion, we must determine the heat capacity of the calorimeter setup (including the water and bomb). To do this, a carefully weighed mass of a compound with a known heat of combustion is burned. A common standard is benzoic acid (C₅H₅COOH), a pure, stable crystalline solid. The combustion of benzoic acid releases 26.38 kJ/g. Using the mass of benzoic acid burned and the temperature increase of the calorimeter, we can calculate the heat capacity of the bomb, \(C_{cal}\).

Example \(\PageIndex{5}\): Combustion of Glucose

A bomb calorimeter is first calibrated using 0.579 g of benzoic acid. The combustion of this sample causes the temperature of the calorimeter to increase by 2.08 °C.

After calibration, the calorimeter is recharged with 1.732 g of glucose (C₆H₁₂O₆) and excess oxygen. When the glucose is ignited, the temperature of the calorimeter increases by 3.64 °C.

Given that the combustion of benzoic acid releases 26.38 kJ/g, calculate the change in internal energy (ΔE) for the combustion of glucose in kJ/mol.

Given: mass and ΔT for combustion of benzoic acid and glucose

Asked for: ΔE for combustion of glucose (in kJ/mol)

Strategy:

1. Use the benzoic acid data to find the heat capacity of the calorimeter.
2. Use that heat capacity to calculate the heat released in the combustion of glucose.
3. Find ΔE in kJ/mol by dividing by the number of moles of glucose.

Solution:

A. Calculate heat released by benzoic acid:

\(q_{rxn}=(0.579g)(-26.38kJ/g)=-15.3kJ\)

Note: since heat is released, the value is negative.

Use this value to find the heat capacity of the calorimeter:

\(q_{rxn}=-q_{cal}=-C_{cal} \Delta T \\ C_{cal}=\frac{-q_{cal}}{\Delta T }=\frac{-(-15.3kJ)}{2.08 °C}=7.34 kJ/°C\)

B. Use the heat capacity from A to find the heat released in the combustion of glucose:

 \(q_{rxn}=-q_{cal}=-C_{cal} \Delta T =-7.34 kJ/°C(3.64°C)=-26.7kJ\)

C. Calculate the moles of glucose:

\(\text{mol glucose} = \frac{1.732g}{180.16g/mol}=0.00961 mol\)

Convert to kJ/mol

\(ΔE = \frac{-26.7kJ}{0.00961 mol}=-2780\; kJ/mol\)

Exercise \(\PageIndex{6}\): Combustion of Methlhydrazine

Methylhydrazine is used as a rocket fuel.

To find the heat associated with this fuel, a bomb calorimeter is first calibrated using 2.123 g of benzoic acid. The combustion of this sample causes the temperature of the calorimeter to increase by 4.75 °C.

After calibration, the calorimeter is recharged with 1.932 g of methylhydrazine (CH₃NHNH₂) and excess oxygen. When the methylhydrazine is ignited, the temperature of the calorimeter increases by 4.64 °C.

Given that the combustion of benzoic acid releases 26.38 kJ/g, calculate the change in internal energy (ΔE) for the combustion of methylhydrazine in kJ/mol.

 

Answer

A. Calculate heat released by benzoic acid:

\(q_{rxn}=(2.123g)(-26.38kJ/g)=-56.0kJ\)

Note: since heat is released, the value is negative.

Use this value to find the heat capacity of the calorimeter:

\(q_{rxn}=-q_{cal}=-C_{cal} \Delta T \\ C_{cal}=\frac{-q_{cal}}{\Delta T }=\frac{-(-56.0kJ)}{4.75 °C}=11.8 kJ/°C\)

B. Use the heat capacity from A to find the heat released in the combustion of methylhydrazine:

 \(q_{rxn}=-q_{cal}=-C_{cal} \Delta T =-11.8 kJ/°C(4.64°C)=-54.7kJ\)

C. Calculate the moles of methylhydrazine:

\(\text{mol methylhydrazine} = \frac{1.932g}{46.07g/mol}=0.00419 mol\)

Convert to kJ/mol

\(ΔE = \frac{-54.7kJ}{0.00419 mol}=-1300\; kJ/mol\)

Chemistry in Everyday Life: Measuring Nutritional Calories

You’ve probably seen energy listed on food labels in Calories. But what exactly is a Calorie?

In science, 1 calorie (cal) is defined as the amount of energy needed to raise the temperature of 1 gram of water by 1 °C. One Calorie (with a capital C), also known as a nutritional Calorie, is equal to 1000 cal, or 1 kilocalorie (kcal). This is about the amount of energy needed to raise the temperature of 1 kg of water by 1 °C.

The energy content of food comes from the macronutrients: carbohydrates, proteins, and fats. On average:

•     Carbohydrates provide 4 Calories per gram
•     Proteins provide 4 Calories per gram
•     Fats provide 9 Calories per gram

These values are reflected on nutrition labels (Figure \(\PageIndex{4}\)).

Figure \(\PageIndex{4}\): (a) Macaroni and cheese contain energy in the form of the macronutrients in the food. (b) The food’s nutritional information is shown on the package label. (credit a: modification of work by “Rex Roof”/Flickr)

For the example shown in (b), a 1-cup serving of macaroni and cheese contains 5 g protein, 31 g carbohydrates and 12 g fat.

We can estimate the total energy using average values for each macronutrient:
(5 g protein × 4 Cal/g) + (31 g carbs × 4 Cal/g) + (12 g fat × 9 Cal/g) = 252 Cal

This aligns closely with the 250 Calories shown on the label.

Where do these numbers come from?

Originally, the caloric content of food was measured using bomb calorimetry: the food is dried, ground, and formed into a pellet, which is then combusted in a bomb calorimeter to measure the energy released.

Today, most nutrition labels use the Atwater system, which assigns average energy values to each macronutrient based on calorimetry data from real foods. For example, the energy from carbohydrates is adjusted to subtract fiber (which isn’t digested and doesn’t contribute Calories). The final caloric value is calculated from the amounts of each nutrient in the food.

Summary

Calorimetry is a set of techniques used to measure heat changes during chemical processes. It uses devices called calorimeters, which detect temperature changes during a chemical reaction. The size of the temperature change depends on both the amount of heat transferred and the heat capacity of the system.

•     Heat capacity (C) is the energy needed to raise the temperature of an object by 1 °C (units: J/°C).
•     Specific heat capacity (c) is the energy needed to raise the temperature of 1 g of a substance by 1 °C (units: J/g·°C).
•     Molar heat capacity (Cₘ) is the energy needed to raise the temperature of 1 mol of a substance by 1 °C (units: J/mol·°C).

Water has a very high specific heat, which helps regulate temperature in the environment and in living organisms.

According to the law of conservation of energy, any heat released or absorbed by a system must be absorbed or released by the surroundings.

Heat measurements are typically made using:

•     Constant-pressure calorimetry: measures heat at constant pressure and gives the enthalpy change, ΔH
  •   q_p = ΔH
•    Constant-volume (bomb) calorimetry: used for reactions involving gases, such as combustion, and gives the change in internal energy, ΔE
  •   q_v = ΔE