4.E: Gases (Exercises)

States of Matter

Exercise \(\PageIndex{1}\)**

For a substance that has gas, liquid, and solid phases, arrange these phases in order of

a) increasing density

b) compressibility

c) molecular motion.

Answer

a) gas < liquid < solid

For most substances, density increases from gas to liquid to solid. However, there are exceptions.  Water, for example, is less dense as a solid (ice) than as a liquid.

b) solid < liquid < gas

Gases are much more compressible than liquids or solids. Solids are generally the least compressible.

c) solid < liquid < gas

Molecular motion increases with temperature and phase. In solids, particles vibrate in place; in liquids, they move more freely; and in gases, they move rapidly and randomly.

Gas Pressure

Exercise \(\PageIndex{2}\)**

Why are sharp knives more effective than dull knives (Hint: think about the definition of pressure)?

Answer

The cutting edge of a knife that has been sharpened has a smaller surface area than a dull knife. Since pressure is force per unit area, a sharp knife will exert a higher pressure with the same amount of force and cut through material more effectively.

Exercise \(\PageIndex{3}\)*

Atmospheric pressure in Vancouver, BC was 102.3 kPa. Calculate this barometric pressure in atm and mm Hg.

Answer

\[ 102.3 \text{ kPa} \left(\dfrac{1 \text{ atm}}{101.325 \text{ kPa}}\right) = 1.010 \text{ atm}\nonumber \]

\[ 102.3 \text{ kPa} \left(\dfrac{760 \text{ mmHg}}{101.325 \text{ kPa}}\right) = 767.3 \text{ mmHg}\nonumber \]

Exercise \(\PageIndex{4}\)*

The pressure of the atmosphere on the surface of the planet Venus is about 88.8 atm. What is this pressure in mmHg?

Answer

\[ 88.8 \text{ atm} \left(\dfrac{760 \text{ mmHg}}{1 \text{ atm}}\right) = 67500 \text{ mmHg}\nonumber \]

 

Exercise \(\PageIndex{5}\)**

The pressure of a sample of gas is measured at sea level with a closed-end manometer as shown in the figure below. The liquid in the manometer is mercury. Determine the pressure of the gas in:

1. mmHg
2. atm

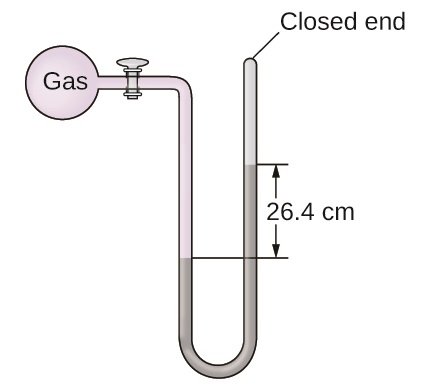
Answer

a. Converting from cm to mm, we obtain 264 mmHg as a height difference between two arms.  Since this is a closed-end manometer, the height difference gives the pressure of the gas.

b. \[264 \text{ mmHg}\left(\dfrac{1 \text{ atm}}{760 \text{ mmHg}}\right)=0.347 \text{ atm}\nonumber\]

Exercise \(\PageIndex{6}\)**

The pressure of a sample of gas is measured at sea level with an open-end mercury manometer. Assuming atmospheric pressure is 760.0 mm Hg, determine the pressure of the gas in:

1. mm Hg
2. atm

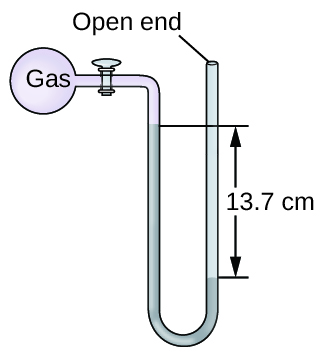
Answer

a. Converting from cm to mm, we obtain 137 mmHg as a height difference between two arms. The gas pressure is less than atmospheric pressure since the level of the mercury is higher on the left side (gas side) than the right side (open to atmosphere). 

760 mmHg - 137 mmHg = 623 mmHg

b.  \[623 \text{ mmHg}\left(\dfrac{1 \text{ atm}}{760 \text{ mmHg}}\right)=0.820\text{ atm}\nonumber\]

 

Relating Pressure, Volume, Amount, and Temperature: The Ideal Gas Law

Exercise \(\PageIndex{7}\)*

When a scuba diver exhales gas bubbles, the bubbles rise through the column of water going from higher to lower pressure. Explain how the volume of the bubbles change as they rise to the surface, assuming that they remain intact.

Answer

As the bubbles rise, the pressure decreases, so their volume increases.

Exercise \(\PageIndex{8}\)*

Calculate the volume of 1.00 mol of CH₄ gas at 150.0 K and 1.00 atm

Answer

\[V=\dfrac{nRT}{P} = \dfrac{(1.00 \,mol)(0.08206\dfrac{L \cdot atm}{mol \cdot K})(150.0\,K)}{1.00\,atm}=12.3\,L \nonumber\]

 

Exercise \(\PageIndex{9}\)*

What is the temperature of an 11.2-L sample of carbon monoxide, CO, at 744 torr if it occupies 13.3 L at 55 °C and 744 torr?

Answer

276 K

Solution

\[\dfrac{P_iV_i}{n_iT_i}=\dfrac{P_fV_f}{n_fT_f}\nonumber \]

Since the sample of CO gas is the same n_i = n_f, so we cancel those from the equation.

\[\dfrac{P_iV_i}{\cancel{n_i}T_i}=\dfrac{P_fV_f}{\cancel{n_f}T_f}\nonumber \]

 Solving  for \(T_i\):

\(T_i = \dfrac{P_iV_iT_f}{P_fV_f}\)

Where:

\(P_i = 744\: torr\)

\(V_i = 11.2\: L\)

\(P_f = 744\: torr\)

\(V_f = 13.3\: L\)

\(T_f = 328\: K\)

\(\dfrac{(744\: torr)(11.2\: L)(328\: K)}{(744\: torr)(13.3\: L)} = 276 \: K\)

Exercise \(\PageIndex{10}\)*

A 2.50-L volume of hydrogen measured at –196 °C is warmed to 100 °C. Calculate the volume of the gas at the higher temperature, assuming no change in pressure.

Answer

\[\dfrac{P_iV_i}{n_iT_i}=\dfrac{P_fV_f}{n_fT_f}\nonumber \]

Since the sample of H₂ gas is the same n_i = n_f and there is no change in pressure, so P_i=P_f.

\[\dfrac{\cancel{P_i}V_i}{\cancel{n_i}T_i}=\dfrac{\cancel{P_f}V_f}{\cancel{n_f}T_f}\nonumber \]

\[\dfrac{V_i}{T_i}=\dfrac{V_f}{T_f}\nonumber \]

\[V_f=\dfrac{V_iT_f}{T_i}=\dfrac{(2.50\:L)(373\:K)}{(77\:K)}=12.1\:L \nonumber \]

Exercise \(\PageIndex{11}\)**

How many moles of gaseous boron trifluoride, \(\ce{BF3}\), are contained in a 4.3410 L bulb at 788.0 K if the pressure is 1.220 atm? How many grams of \(\ce{BF3}\)?

Answer

Use the ideal gas law:

\[n=\dfrac{PV}{RT}=\dfrac{(1.220\:atm)(4.3410\:L)}{(0.08206\dfrac{L \cdot atm}{mol \cdot K})(788.0\:K)}=0.08190\:mol \nonumber  \]

Convert moles to grams using the molar mass of \(\ce{BF3}\) (67.81 g/mol):

\[0.08190\:mol(67.81\dfrac{g}{mol})=5.553\:g \nonumber\]

Exercise \(\PageIndex{12}\)*

A balloon that is 100.21 L at 21 °C and 0.981 atm is released and just barely clears the top of Blue Mountain in Ontario. If the final volume of the balloon is 144.53 L at a temperature of 5 °C, what is the pressure experienced by the balloon as it clears Blue Mountain?

Answer

\[\dfrac{P_iV_i}{n_iT_i}=\dfrac{P_fV_f}{n_fT_f}\nonumber \]

n_i = n_f, so we can cancel those from the equation:

\[\dfrac{P_iV_i}{\cancel{n_i}T_i}=\dfrac{P_fV_f}{\cancel{n_f}T_f}\nonumber \]

\[P_f=\dfrac{P_iV_iT_f}{T_iV_f}\nonumber \]

\[P_f=\dfrac{(0.981 \: atm)(100.21 \: L)(278 \: K)}{(144.53 \: L)(294 \: K)}=0.643 \: atm\nonumber \]

Exercise \(\PageIndex{13}\)**

Iodine, I₂, is a solid at room temperature but sublimes (converts from a solid into a gas) when warmed. What is the temperature in a 73.3-mL bulb that contains 0.292 g of I₂ vapor at a pressure of 0.462 atm?

Answer

359 K

Solution

Use the equation \(PV =nRT\) and solve for \(T\)

\(T= \dfrac{PV}{nR}\)

Convert grams of I₂ to moles of I₂ and convert mL to L

\(0.292\: g\: \ce{I2}\times \dfrac{1\: mole\: \ce{I2}}{253.8\: g\: \ce{I2}} = 1.15 \times10^{-3}\: mol\: \ce{I2}\)

\(73.3\:mL = 0.0733\:L\)

Use these values along with \(R= 0.08206\: \dfrac{atm \cdot L}{mol \cdot K}\) to solve for \(T\)

\(T= \dfrac{(0.462\: \cancel{atm})(0.0733\:\cancel{L})}{(1.15\times10^{-3}\: \cancel{mol})(0.08206\: \dfrac{\cancel{atm} \cdot \cancel{L}}{\cancel{mol} \cdot K})} = 359\: K \)

Exercise \(\PageIndex{14}\)**

A 20.0-L cylinder containing 11.34 kg of butane, C₄H₁₀, was opened to the atmosphere. Calculate the mass of the gas remaining in the cylinder if it were opened and the gas escaped until the pressure in the cylinder was equal to the atmospheric pressure, 0.983 atm, and a temperature of 27 °C.

Answer

To find the mass of butane, we need to find the moles of butane left in the cylinder:

\[n = \dfrac{PV}{RT}=\dfrac{(0.983\:atm)(20.0\:L)}{(0.08206\dfrac{L \cdot atm}{mol \cdot K})(300 \: K)}=0.799\:mol \nonumber\]

The molar mass of butane, 58.12 g/mol, can be used to find the mass.

\[0.799\:mol\:C_4H_{10}\:(58.12\dfrac{g}{mol})=46.4g \nonumber\]

Exercise \(\PageIndex{15}\)**

For a given amount of gas showing ideal behaviour, draw labelled graphs of:

1. the variation of \(P\) with \(V\)
2. the variation of \(V\) with \(T\)
3. the variation of \(P\) with \(T\)
4. the variation of \(\dfrac{1}{P}\) with \(V\)

Answer

For a gas exhibiting ideal behaviour:

Exercise \(\PageIndex{16}\)*

If the volume of a fixed amount of an ideal gas is tripled at constant temperature, what happens to the pressure?

Answer

The pressure decreases by a factor of 3.

Exercise \(\PageIndex{17}\)**

Your instructor blows up a balloon so that it is filled with 0.55 moles of helium at 21.5 ^oC and 1.00 atm pressure. The instructor adds 0.050 moles of helium to the balloon. If the pressure in the balloon remains the same, do you expect the volume to increase or decrease? Explain your reasoning in clear and complete statements.

Answer

Volume is predicted to increase. The addition of more gas (at the same volume) would result in more collisions and an increase in pressure.  For pressure to remain constant, the volume would have to increase, so that the number of collisions per unit area of the balloon is the same.  Increasing volume affects the collisions by increasing the surface area of the balloon and by increasing the average distance the He atoms have to travel to collide with the balloon wall.

Exercise \(\PageIndex{18}\)**

A 8.60 L tank of nitrogen gas at a pressure of 455 mmHg is connected to an empty tank with a volume of 5.35 L. What is the final pressure (in atm) in the system after the valve connecting the two tanks is opened? Assume that the temperature is constant.

Answer

Before performing the calculation, predict whether you expect the pressure to increase or decrease with the change in volume.

\[\dfrac{P_iV_i}{n_iT_i}=\dfrac{P_fV_f}{n_fT_f}\nonumber \]

n_i = n_f and T_i = T_f, so we can cancel those from the equation:

\[\dfrac{P_iV_i}{\cancel{n_i}\cancel{T_i}}=\dfrac{P_fV_f}{\cancel{n_f}\cancel{T_f}}\nonumber \]

\[P_iV_i=P_fV_f\nonumber \]

\[P_f=\dfrac{P_iV_i}{V_f}=\dfrac{(455\:mmHg)\dfrac{1 \: atm}{760 \: mmHg}(8.60\:L)}{(8.60\:L+5.35\:L)}=0.369\:atm\nonumber \]

Don't forget to convert the pressure from mmHg to atm.

Exercise \(\PageIndex{19}\)**

The average respiratory rate for adult humans is 20 breaths per minute. If each breath has a volume of 310 mL of air at 20°C and 0.997 atm, how many moles of air does a person inhale each day?

Answer

First, find the number of breaths taken each day:

\[ 1 \text { day }\left(\frac{24 \text { h}}{\text {day}}\right)\left(\frac{60 \text { min}}{\text{h}}\right)\left(\frac{20 \text { breaths}}{\text {min}}\right)=28800 \text { breath/day } \nonumber\]

Next, calculate the moles in each breath.

\[n=\frac{P V}{R T}=\frac{(0.997 \mathrm{~atm})(0.310 \mathrm{~L})}{\left(0.08206 \frac{\text{L} \cdot \text{atm}}{\text{mol} \cdot \text{K}}\right)(293 \mathrm{~K})}=0.0129 \mathrm{~mol} \nonumber\]

Finally, multiply to get the moles per day:

\[\left(0.0129 \frac{\mathrm{~mol}}{\text { breath }}\right)\left(28800 \frac{\text { breath }}{\text { day }}\right)=370 \frac{\mathrm{~mol}}{\text { day }}\nonumber
 \]

Applications of the Gas Laws

Exercise \(\PageIndex{20}\)**

Calculate the density of Freon 12, CF₂Cl₂, at 30.0 °C and 0.954 atm.

Answer

To find the density we need mass/volume, g/L.  From the ideal gas equation, we can find moles/volume and then use the molar mass to find the density.

Rearranging the ideal gas equation:

\[ \frac{n}{V}=\frac{P}{R T} \nonumber \]

Paying attention to units, solve for n/V:
\[ \frac{n}{V}  = \frac{0.954 \: atm}{\left(0.08206 \frac{L \cdot atm}{mol \cdot K}\right)(303 \:K)} = 0.0384 \frac{mol} {L} \nonumber \]

Finally, use the molar mass to find the density:
\[0.0384 \frac{\cancel{mol}}{L}\left(120.91 \frac{g}{\cancel{mol}}\right)=4.64 \frac{g}{L} \nonumber \]

Exercise \(\PageIndex{21}\)**

What is the molar mass of a gas if 0.0494 g of the gas occupies a volume of 0.100 L at a temperature 26 °C and a pressure of 307 Torr?

Answer

30.0 g/mol

Solution

Convert Torr to atm and °C to K

\(307\:Torr=0.404\:atm\)

\(26\:°C= 299\:K\)

2.) Use the equation \(PV=nRT\) and solve for \(n\)

\(n=\dfrac{PV}{RT}\)

\(n=\dfrac{(0.404\:\cancel{atm})(0.100\:\cancel{L})}{(0.08206\dfrac{\cancel{atm}\cdot\cancel{L}}{mol\cdot\cancel{K}})(299\cancel{K})}=0.00165\:mol\)

3.) Then divide grams by the number of moles to obtain the molar mass:

\(\dfrac{0.0494\:g}{0.00165\:mol}=30.0\dfrac{g}{mol}\)

Exercise \(\PageIndex{22}\)**

What is the molar mass of a gas if 0.281 g of the gas occupies a volume of 125 mL at a temperature 126 °C and a pressure of 777 Torr?

Answer

Convert units as needed:

\(777\:Torr=1.02\:atm\)

\(126\:°C= 399\:K\)

\(125\:mL = 0.125\:L\)

2.) Use the equation \(PV=nRT\) and solve for \(n\)

\(n=\dfrac{PV}{RT}\)

\(n=\dfrac{(1.02\:\cancel{atm})(0.125\:\cancel{L})}{(0.08206\dfrac{\cancel{atm}\cdot\cancel{L}}{mol\cdot\cancel{K}})(399\cancel{K})}=0.00390\:mol\)

3.) Then divide grams by the number of moles to obtain the molar mass:

\(\dfrac{0.281\:g}{0.00390\:mol}=72.0\dfrac{g}{mol}\)

Exercise \(\PageIndex{23}\)**

The density of a certain gaseous fluoride of phosphorus is 3.93 g/L at 0.00 ^oC and 1.00 atm. Calculate the molar mass of this gas.  Which is the most likely identity of the gas: PF₃, PF₅, or P₂F₄?

Answer

We know the pressure and temperature, which allows us to find how many moles 1 L of this gas contains (mol/L).  We can use this, along with the density, to find the molar mass.

Paying attention to units, solve for n/V:
\[ \frac{n}{V}=\frac{1.00\:atm}{\left(0.08206 \frac{L \cdot atm}{mol \cdot K}\right)(273.15 \:K)}=0.0446 \frac{mol}{L} \nonumber \]

A 1 L sample would have a mass of 3.93 g (from the density) and contain 0.0446 mol (from the calculation we just did).

\[\frac{3.93 \: g}{0.0446 \: mol}=88.1 \: g/mol \nonumber \]

The gas is most likely PF₃.

Exercise \(\PageIndex{24}\)**

Pure oxygen was first prepared by heating mercuric oxide, HgO:

\(\ce{2HgO}(s)⟶\ce{2Hg}(l)+\ce{O2}(g)\)

What volume of O₂ at 23 °C and 0.975 atm is produced from the decomposition of 5.36 g of HgO?

Answer

First find the moles of HgO and the moles of O₂ produced in the reaction:
\[5.36 \mathrm{~g} \: \mathrm{HgO}\left(\frac{\mathrm{~mol}}{216.59 \mathrm{~g}}\right)\left(\frac{1 \mathrm{~mol} \mathrm{~O}_2}{2 \mathrm{~mol} \: \mathrm{HgO}}\right)=0.0124 \mathrm{~mol} \: \mathrm{O}_2 \nonumber \]

Once we have the moles of O₂ produced, we can use the ideal gas equation to find the volume of the gas:
\[V=\frac{n R T}{P} =\frac{(0.0124 \mathrm{~mol})(0.08206 \frac{\mathrm{L} \cdot \mathrm{atm}}{\mathrm{mol} \cdot \mathrm{K}})(296 \mathrm{~K})}{0.975 \mathrm{~atm}} =0.309 \mathrm{~L} \nonumber \]

Exercise \(\PageIndex{25}\)**

The chlorofluorocarbon CCl₂F₂ can be recycled into a different compound by reaction with hydrogen to produce CH₂F₂, a compound useful in chemical manufacturing:

\[\ce{CCl2F2}(g)+\ce{4H2}(g)⟶\ce{CH2F2}(g)+\ce{2HCl}(g) \nonumber\]

What volume of hydrogen at 225 atm and 35.5 °C would be required to react with 1 ton (1.000 × 10³ kg) of CCl₂F₂?

Answer

First find the moles of CCl₂F₂ and the moles of H₂ needed to react with the CCl₂F₂:
\[1.000\times 10^3 \mathrm{~kg} \: \mathrm{CCl_2F_2}\left(\frac{1000 \mathrm{~g}}{\mathrm{kg}}\right)\left(\frac{\mathrm{~mol}}{120.91 \mathrm{~g}}\right)\left(\frac{4 \mathrm{~mol} \mathrm{~H}_2}{1 \mathrm{~mol} \mathrm{~CCl_2F_2}}\right)=33082 \mathrm{~mol} \mathrm{~H}_2 \nonumber \]

Once we have the moles of H₂ produced, we can use the ideal gas equation to find the volume of the gas:
\[V=\frac{n R T}{P} =\frac{(33082 \mathrm{~mol})(0.08206 \frac{\mathrm{L} \cdot \mathrm{~atm}}{\mathrm{mol} \cdot \mathrm{~K}})(308.7 \mathrm{~K})}{225 \mathrm{~atm}} =3.72 \times 10^3 \mathrm{~L} \nonumber \]

Exercise \(\PageIndex{26}\)**

What volume of oxygen is required to react with 12.00 L of ethane gas, C₂H₆, to produce carbon dioxide and water, if the volumes of C₂H₆ and O₂ are measured under the same conditions of temperature and pressure?

\[\ce{2C2H6}(g)+\ce{7O2}(g)⟶\ce{4CO2}(g)+\ce{6H2O}(g) \nonumber\]

Answer

Since the temperature and pressure are constant, the volumes of the gases are directly proportional to the number of moles present:

\[V=\frac{n R T}{P} = constant \times n \nonumber \]

This means we can consider the stoichiometry of the reaction in terms of volumes:

\[12.00\mathrm{~L} \:\ce{C2H6}\left(\frac{7\mathrm{~mol}\:\ce{O2}}{2\mathrm{~mol}\:\ce{C2H6}} \right)=42.00 \mathrm{~L}\:\ce{O2} \nonumber \]

Gas Mixtures and Partial Pressures

Exercise \(\PageIndex{27}\)**

A 36.0 L cylinder of a gas used for calibration of blood gas analyzers in medical laboratories contains 350 g CO₂, 805 g O₂, and 4880 g N₂. At 25 °C, what is the pressure in the cylinder in atmospheres?  What is the mole fraction of O₂ in the mixture?  What is the partial pressure of O₂?

Answer

We can find the total pressure from the total moles of gas.  First, convert the mass of each gas to moles and then use the ideal gas equation to find pressure:

$$
\begin{aligned}
& 350 \mathrm{~g} \mathrm{~CO}_2\left(\frac{\mathrm{~mol}}{44.01 \mathrm{~g}}\right)=7.95 \mathrm{~mol} \\
& 805 \mathrm{~g} \mathrm{~O}_2\left(\frac{\mathrm{~mol}}{32.0 \mathrm{~g}}\right)=25.2 \mathrm{~mol} \\
& 4880 \mathrm{~g} \mathrm{~N}_2\left(\frac{\mathrm{~mol}}{28.02 \mathrm{~g}}\right)=174.2 \mathrm{~mol} \\
& n_{\text {tot }}=7.95 \mathrm{~mol}+25.2 \mathrm{~mol}+174.2 \mathrm{~mol}=207.4 \mathrm{~mol} \\
& P_{\text {tot}}=\frac{n_{\text {tot}} R T}{V}=\frac{\left.(207.4 \mathrm{~mol})(0.08206 \frac{\mathrm{L}\cdot\mathrm{atm}}{\mathrm{mol} \cdot \mathrm{K}}\right)(298 \mathrm{~K})}{36.0 \mathrm{~L}}=141 \mathrm{~atm}
\end{aligned}
$$

$$
\begin{aligned}
& \chi_A=\frac{\mathrm{mol}_A}{\text {mol}_{tot}} \\
& \chi_{\mathrm{O}_2}=\frac{25.2 \mathrm{~mol}}{207.4 \mathrm{~mol}}=0.122 \\
& P_A=\chi_A \times P_{\text {tot }} \\
& P_{\mathrm{O}_2}=(0.122)(141 \mathrm{~atm})=17.2 \mathrm{~atm}
\end{aligned}
$$

Exercise \(\PageIndex{28}\)*

A sample of gas isolated from unrefined petroleum contains 90.0% CH₄, 8.9% C₂H₆, and 1.1% C₃H₈ at a total pressure of 3.03 atm. What is the partial pressure (in atm) of each component of this gas?

Answer

The percentages can be converted to mole fractions.  90.0% CH₄ means that the mole fraction of CH₄ is 0.900.

\[P_A=\chi_A \times P_{\text {tot }} \nonumber \]

\[P_{\ce{CH4}}=0.900(3.03\:atm) =2.73\:atm \nonumber \]

\[P_{\ce{C2H6}}=0.089(3.03\:atm) =0.27\:atm \nonumber \]

\[P_{\ce{C3H8}}=0.011(3.03\:atm) =0.033\:atm \nonumber \]

Exercise \(\PageIndex{29}\)**

A 2.00 L container with 2.50 atm of N₂ is connected to a 5.00 L container with 1.90 atm of He. The containers are opened, and the gases mix. What is the final pressure inside the containers?  Assume there is no change in temperature.

Answer

Because gases act independently of each other, we can determine the resulting final pressures of each gas (to reflect the change in volume) and then add the two resulting pressures together to get the final pressure. The total final volume is 2.00 L + 5.00 L = 7.00 L. First, determine the final pressure of N₂:

(2.50 atm)(2.00 L) = P_f(7.00 L)

Solving for P_f, we get P_f = 0.714 atm = partial pressure of N₂.

Now we do the same thing for the He:

(1.90 atm)(5.00 L) = P_f(7.00 L)       P_f = 1.36 atm = partial pressure of He

The total pressure is the sum of the two partial pressures:

P_tot = 0.714 atm + 1.36 atm = 2.07 atm

Exercise \(\PageIndex{30}\)*

Consider the gas mixture of H₂ and Ar shown below:

Which gas has the greater mole fraction?  Which gas has the greater partial pressure?

Answer

There are more particles of H₂ than of Ar, so H₂ has the higher mole fraction and partial pressure.

The Kinetic-Molecular Theory

Exercise \(\PageIndex{31}\)**

A 1-L sample of CO initially at 0 ^oC and 1 atm is heated to 546 K at constant volume.

1. What effect do these changes have on the number of collisions of the molecules of the gas per unit area of the container wall?
2. What is the effect on the average kinetic energy of the molecules?
3. What is the effect on the root mean square speed of the molecules?

Answer

a. The number of collisions per unit area of the container wall increases.

Since the gas is heated at constant volume, the molecules move faster and collide with the container walls more often. This leads to more frequent collisions per unit area.

b. The average kinetic energy increases.

The average kinetic energy of a gas is directly proportional to its absolute temperature (in kelvin).

c. The root mean square speed increases.

The rms speed is proportional to the square root of the temperature. Since the temperature increases, the rms speed increases as well.

Exercise \(\PageIndex{32}\)*

Calculate the root-mean-square speed of nitrogen, N₂, molecules in an air sample at 25 ^oC.

Answer

\[u_\ce{rms}=\sqrt{\dfrac{3RT}{ℳ}} \nonumber \]

\[u_\ce{rms}=\sqrt{\dfrac{3(8.314\dfrac{\cancel{kg} \cdot m^2}{\cancel{mol} \cdot s^2 \cdot \cancel{K}})(298\cancel{K})}{28.02\dfrac{\cancel{g}}{\cancel{mol}}}\left(\dfrac{1000\cancel{g}}{\cancel{kg}}\right)}=515m/s \nonumber \]

 

Exercise \(\PageIndex{33}\)**

What is the ratio of root-mean-square speed values for helium to xenon at 30 ^oC? Which has a higher root-mean-square speed and why?

Answer

\[u_\ce{rms}=\sqrt{\dfrac{3RT}{ℳ}} \nonumber \]

\[u_\ce{rmsHe}=\sqrt{\dfrac{3RT}{ℳ_{He}}} \nonumber \]

\[u_\ce{rmsXe}=\sqrt{\dfrac{3RT}{ℳ_{Xe}}} \nonumber \]

\[\frac{u_\ce{rmsHe}}{u_\ce{rmsXe}}=\frac{\sqrt{\dfrac{3RT}{ℳ_{He}}}}{\sqrt{\dfrac{3RT}{ℳ_{Xe}}}} \nonumber \]

\[\frac{u_\ce{rmsHe}}{u_\ce{rmsXe}}=\frac{\sqrt{\dfrac{\cancel{3RT}}{ℳ_{He}}}}{\sqrt{\dfrac{\cancel{3RT}}{ℳ_{Xe}}}}= \sqrt{\dfrac{ℳ_{Xe}}{ℳ_{He}}}=\sqrt{\dfrac{131.3 \: g/mol}{4.003 \: g/mol}}=5.73\nonumber \]

He has a higher root-mean-square speed by a factor of 5.73 compared to Xe.  He is faster because it has a smaller molar mass.

Exercise \(\PageIndex{34}\)**

Consider two 1 L containers of gas, both at 1 atm and 298 K.  One container contains He and one CH₄.

Compare the two gases in terms of

a. mass

b. density

c. average kinetic energy

d. average speed

e. collision frequency

Answer

a. Since the volume, temperature, and pressure of the two gases are the same, they have the same number of moles.  Since CH₄ has a larger molar mass, the mass is greater for the CH₄ gas.

b. Given the volume is the same for the two gases, the CH₄ gas has a higher density since it has a greater mass.

c. Both gases are at the same temperature, so their average kinetic energies are the same.

d. At the same temperature, the lighter gas, He, moves faster.

e. The collision frequency is the same, since the temperature, volume and number of moles are the same for both gases.

Exercise \(\PageIndex{35}\)*

Which of the following gases diffuse more slowly than oxygen? F₂, Ne, N₂O, C₂H₂, NO, Cl₂, H₂S

Answer

The rate of diffusion is proportional to the speed.  Heavier gases move more slowly.  Any gas with a higher molar mass than O₂ will diffuse more slowly.

F₂, N₂O, Cl₂, H₂S

Additional Problems

Exercise \(\PageIndex{36}\)***

A 2.00 L flask originally contains 1.00 g of ethane (C₂H₆) and 32.0 g of oxygen at 21°C. During ignition, the ethane reacts completely with oxygen to produce CO₂ and water vapor, and the temperature of the flask increases to 200°C. Determine the total pressure before and after the reaction.

\[\ce{2C2H6}(g)+\ce{7O2}(g)⟶\ce{4CO2}(g)+\ce{6H2O}(g) \nonumber\]

Answer

Before reaction:

We can find the total pressure by finding the total moles of gas present:

$$
\begin{aligned}
& 1.00 \mathrm{~g} \mathrm{~\ce{C2H6}} \left(\frac{\mathrm{~mol}}{30.07 \mathrm{~g}}\right)=0.0333 \mathrm{~mol} \ce{~C2H6} \\
& 32.0 \mathrm{~g} \mathrm{~O}_2\left(\frac{\mathrm{~mol}}{32.0 \mathrm{~g}}\right)=1.00 \mathrm{~mol} \\
& n_{\text {tot }}=0.0333 \mathrm{~mol}+1.00 \mathrm{~mol}=1.03 \mathrm{~mol} \\
& P_{\text {tot}}=\frac{n_{\text {tot}} R T}{V}=\frac{\left.(1.03 \mathrm{~mol})(0.08206 \frac{\mathrm{L} \cdot \mathrm {atm}}{\mathrm{mol} \cdot \mathrm {K}}\right)(294 \mathrm{~K})}{2.00 \mathrm{~L}}=12.5 \mathrm{~atm}
\end{aligned}
$$

After the reaction:

We need to know how many moles are present of each reactant and product.

All of the C₂H₆ reacts since there is a big excess of O₂, so C₂H₆ does not contribute to the pressure.

The amount of O₂ that reacts can be found as follows:

\[0.0333\mathrm{~mol} \ce{~C2H6}\left(\frac{7\mathrm{~mol} \ce{~O2}}{2\mathrm{~mol} \ce{~C2H6}}\right)=0.117\mathrm{~mol} \ce{~O2} \nonumber\]

So the amount left after the reaction is 1.00 mol - 0.117 mol = 0.883 mol O₂.

CO₂ and H₂O gases are formed from the reaction:

\[0.0333 \mathrm{~mol} \ce{~C2H6}\left(\frac{4\mathrm{~mol} \ce{~CO2}}{2\mathrm{~mol} \ce{~C2H6}}\right)=0.0666\mathrm{~mol} \ce{~CO2} \nonumber\]

\[0.0333\mathrm{~mol} \ce{~C2H6}\left(\frac{6\mathrm{~mol} \ce{~H2O}}{2\mathrm{~mol} \ce{~C2H6}}\right)=0.0999\mathrm{~mol} \ce{~H2O} \nonumber\]

We can find the total moles to find the total pressure.  Don't forget that the temperature has also increased.

\[n_{\text {tot}}=0.883 \mathrm{~mol}+0.0666 \mathrm{~mol} + 0.0999\mathrm{~mol}=1.05 \mathrm{~mol} \\
P_{\text {tot}}=\frac{n_{\text {tot}} R T}{V}=\frac{\left.(1.05 \mathrm{~mol})(0.08206 \frac{\mathrm{L} \cdot \mathrm {atm}}{\mathrm{mol} \cdot \mathrm {K}}\right)(473 \mathrm{~K})}{2.00 \mathrm{~L}}=20.3 \mathrm{~atm} \nonumber \]

Exercise \(\PageIndex{37}\)**

A steel cylinder of compressed argon with a volume of 0.400 L was filled to a pressure of 145 atm at 10°C. At 1.00 atm pressure and 25°C, how many 15.0 mL incandescent light bulbs could be filled from this cylinder? (Hint: find the number of moles of argon in each container.)

Answer

We can find out how many moles of Ar are needed to fill each lightbulb:

\[n=\dfrac{PV}{RT}=\dfrac{(1.00 \: atm)(0.0150 \:L)}{(0.08206\dfrac{L \cdot atm}{mol \cdot  K})(298 \: K)}=6.13×10^{-4}\:mol \nonumber  \]

We can also calculate the moles of Ar in the cylinder:

\[n=\dfrac{PV}{RT}=\dfrac{(145 \: atm)(0.400 \: L)}{(0.08206\dfrac{L \cdot atm}{mol \cdot  K})(283 \: K)}=2.50  \: mol  \nonumber \]

We take the moles from the cylinder and divide by the moles needed for each light bulb to find how many lightbulbs can be filled:

\[\dfrac{2.50 \: mol}{6.13×10^{-4} \: mol}=4.08×10^3 \mathrm{~lightbulbs} \nonumber\]

Exercise \(\PageIndex{38}\)**

Most mixtures of hydrogen gas with oxygen gas are explosive. However, a mixture that contains less than 3.0 % O₂ is not. If enough O₂ is added to a cylinder of H₂ at 33.2 atm to bring the total pressure to 34.5 atm, is the mixture explosive?  Assume there is no change in temperature.

Answer

To determine if the mixture is explosive, we need to find the mole fraction of O₂.  We can write the mole fraction as a ratio of the pressure of O₂ to the total pressure, since volume and temperature are constant:

\[\chi_A=\frac{\mathrm{mol}_A}{\text {mol}_{tot}}==\frac{\mathrm{P}_A}{\text {P}_{tot}} \nonumber\]

The pressure of O₂ can be found by subtracting the pressure of H₂ from the total pressure (since the gas mixture consists of only those two gases):

\[P_{\ce{O2}} = 34.5 \: atm - 33.2 \: atm = 1.3 \: atm \nonumber\]

\[\chi_{\ce{O2}}=\frac{1.3 \: atm}{34.5 \: atm}=0.038 \nonumber   \]

The gas mixture contains 3.8% O₂, which is greater than the threshold, so it is explosive.

Exercise \(\PageIndex{39}\)***

A sample of a compound of xenon and fluorine, XeF_n, was put in a bulb with a pressure of 18 mmHg. Hydrogen gas, H₂, was added to the bulb until the pressure was 72 mmHg. Passage of an electric spark through the mixture caused a reaction to occur, producing Xe gas and HF. After the HF was removed by reaction with solid KOH, the final pressure of the Xe gas and unreacted H₂ gas in the bulb was 36 mmHg. What is the formula of the xenon fluoride in the original sample? (Note: Xenon fluorides contain only one xenon atom per molecule.)

Answer

We can set up an equation as follows:
\(\ce{Xe}F_n(g) + \frac{n}{2}\ce{H2}(g)\to \ce{Xe}(g)+ n\ce{HF}(g) \)

Initially, we have 18 mmHg of XeF_n and 54 mmHg of H₂ (72 mmHg - 18 mmHg).

After the reaction, we have unreacted H₂ gas, meaning that XeF_n is the limiting reactant and reacts completely.  Since each XeF_n contains one Xe, we form 18 mmHg of Xe (because we had 18 mmHg of XeF_n).  That means there is 18 mmHg of H₂ leftover (36 mmHg - 18 mmHg), so 36 mmHg (54 mmHg initially - 18 mmHg leftover) of H₂ reacted with 18 mmHg of XeF_n or twice as much H₂ as XeF_n:

\(\ce{Xe}F_n(g) + 2\ce{H2}(g)\to \ce{Xe}(g)+ 4\ce{HF}(g) \)

For this to be true, n must be equal to 4, so the formula is XeF₄.

Exercise \(\PageIndex{40}\)***

At 140°C, the pressure of a diatomic gas, X₂, in a 3.0 L flask is 6.267 atm. The mass of the gas is 88.7 g. What is the most likely identity of the gas?

Answer

To determine the identity of the gas, we need to determine the molar mass, g/mol.  We have the mass in the question, so we will use the ideal gas law to determine the number of moles.

\(n=\dfrac{PV}{RT}\)

\(n=\dfrac{(6.267\:\cancel{atm})(3.0\:\cancel{L})}{(0.08206\dfrac{\cancel{atm} \cdot \cancel{L}}{mol \cdot \cancel{K}})(413\cancel{K})}=0.555\:mol\)

Then divide grams by the number of moles to obtain the molar mass:

\(\dfrac{88.7 \: g}{0.555\:mol}=160\dfrac{g}{mol}\)

Each atom in X₂ has a mass of 80 g/mol, making the gas likely to be Br₂.

Exercise \(\PageIndex{41}\)**

What is the density of laughing gas, dinitrogen monoxide, N₂O, at a temperature of 325 K and a pressure of 113.0 kPa?

Answer

To find the density we need mass/volume, g/L.  From the ideal gas equation, we can find moles/volume and then use the molar mass to find the density.

Rearranging the ideal gas equation:

\[ \frac{n}{V}=\frac{P}{R T} \nonumber \]

Paying attention to units, solve for n/V:
\[ \frac{n}{V}=\frac{(113.0 \mathrm{~kPa})\left(\frac{1 \mathrm{~atm}}{101.325 \mathrm{~kPa}}\right)}{\left(0.08206 \frac{\mathrm{L} \cdot \mathrm{~atm}}{\mathrm{mol} \cdot \mathrm{~K}}\right)(325 \mathrm{~K})}=0.0418 \frac{\mathrm{~mol}}{\mathrm{~L}} \nonumber \]

Finally, use the molar mass to find the density:
\[0.0418 \frac{\cancel{\mathrm{~mol}}}{\mathrm{~L}}\left(44.02 \frac{\mathrm{~g}}{\cancel{\mathrm{~mol}}}\right)=1.84 \frac{\mathrm{~g}}{\mathrm{~L}} \nonumber \]

Exercise \(\PageIndex{42}\)**

The graph below shows the distribution of molecular speeds for two gases, A and B, at the same temperature.

Which of the following statements are true?  Correct any incorrect statements

a)    Gas B and Gas A have the same molar mass.
b)    The average kinetic energy of Gas B is greater than that of Gas A.
c)    The rate of effusion of Gas A would be greater than the rate of effusion of Gas B.
d)    Increasing the temperature will shift both distributions to the right, to higher speeds.
e)    The rate of diffusion of Gas A would be the same as the rate of diffusion of Gas B.

Answer

a) False; Since Gas B moves faster than Gas A, it must have a lower molar mass.

b) False; Since temperature is the same, both gases have the same average kinetic energy.

c) False; The rate of effusion is proportional to the speed. Since Gas B moves faster, Gas B will have the higher rate of effusion.

d) True

e) False; The rate of diffusion is proportional to the speed. Since Gas B moves faster, Gas B will have the higher rate of effusion.