4.2: Pressure

Last updated
Save as PDF

Page ID: 498745

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Describe the pressure of a gas.
Determine the pressure of a gas from a manometer or barometer
Convert between units of pressure.

To fully describe a gas sample, we need four measurable quantities:

temperature (in Kelvins),
volume (in liters),
amount (in moles),
pressure (in atmospheres)

These variables are not independent, meaning that changing one affects the others. If we know three of these values, we can calculate the fourth, giving us a complete physical description of the gas. This section focuses on pressure and how it is measured.

What is Pressure?

When you inflate a balloon, you can feel the air inside pushing against its surface. This happens because gases, like all forms of matter, exert force on the surfaces they touch. A basketball filled with air feels firm because of the force of the collisions of the gas particles against the inner walls. Solid objects, like a book resting on a table, exert gravitational force due to their weight.

Pressure (P) depends on both the force (F) applied and the area (A) over which the force is distributed:

\[P=\dfrac{\rm Force}{\rm Area}=\dfrac{F}{A}\label{4.3.1} \]

The same force applied to a smaller area creates a higher pressure. For example, when using a garden hose, placing a thumb over the opening reduces the area where the water exits. This increases the pressure, making the water spray more forcefully.

The units of pressure come from the units used to measure force and area. In the International System of Units (SI), force is measured in newtons (N), and area in square meters (m²). The standard SI unit for pressure is the pascal (Pa), which is defined as one newton per square meter:

\[\rm 1 \;Pa=1\;N/m^2 \nonumber \]

Atmospheric Pressure

Just as we exert pressure on a surface due to gravity, so do the gases in our atmosphere. The weight of the air above us creates atmospheric pressure, which is substantial. A 1 m² column of air, extending from sea level to the top of the atmosphere, has a mass of about 10,000 kg, resulting in a pressure of approximately 101 kPa:

At sea level, this pressure is equivalent to the weight of a full-grown elephant standing on a doormat or a bowling ball pressing on your thumbnail. Although these comparisons make atmospheric pressure seem immense, life on Earth has evolved under these conditions, so we do not feel the weight of the air around us.

A dramatic demonstration of atmospheric pressure can be seen in this brief video of a railway tanker car imploding. The tanker collapses when its internal pressure is reduced, allowing the much greater atmospheric pressure outside to crush it:

alt

Measuring Atmospheric Pressure: The Barometer

Atmospheric pressure can be measured using a barometer, a device invented in 1643 by Evangelista Torricelli, a student of Galileo. A barometer consists of a long glass tube, sealed at one end, filled with mercury, and inverted into a dish of mercury without allowing air to enter the tube. Some mercury flows out, but a tall column remains inside (Figure $\PageIndex{2}$).

Why doesn’t all the mercury drain from the tube? The answer lies in the balance of forces. Gravity pulls the mercury in the column down, but atmospheric pressure pushes on the surface of the mercury in the dish, forcing mercury up into the tube. Because the space above the mercury column is a vacuum, there is no air pressure inside the tube to push down on the mercury. The column settles at a height where the pressure from the downward force of gravity on the mercury column in the tube exactly balances the pressure of the atmosphere pushing on the Mercury in the dish:

\[
\begin{align*}P_{atmosphere} &= P_{HgColumn} \\[4pt]
\end{align*}\]

The pressure from the Mercury column can be described by the ratio of the gravitational force acting on its mass ($F_g$) and the area at the bottom of the tube ($A$). With further manipulation, we can see that atmospheric pressure can be described from a manometer using only the density of the liquid in the tube ($\rho$), the gravitational acceleration constant ($g$), and the height of the column ($h$):

\[
\begin{align*}P_{atmosphere} &= \dfrac{F_g}{A} \\[4pt]
&= \dfrac{m \cdot g}{A} \\[4pt]
&= \dfrac{\rho \cdot V \cdot g}{A} \\[4pt]
&= \dfrac{\rho \cdot A \cdot h \cdot g}{A} \\[4pt]
&= \rho gh
\end{align*}\]

$F_g$ gravitational force acting on the Mercury column,
$A$ is the area at the bottom of the tube,
$m$ is the mass of the Mercury column in the tube,
$g$ is the gravitational acceleration constant,
$V$ is the volume of the Mercury column in the tube,
$\rho$ is the density of Mercury, and
$h$ is height of the Mercury column.

While we will not calculate the height of mercury columns in CHM 135H, these equations show that the density of the liquid in a barometer affects the height of the column. Mercury is used because of its high density (13.6 g/cm³), which keeps the column height manageable. If a less dense liquid like water were used, the column would have to be over 10 meters tall to balance atmospheric pressure.

Under normal weather conditions at sea level, the mercury column reaches a height of approximately 760 mm above the level of mercury in the dish (Figure $\PageIndex{2}$). This value changes with weather patterns and altitude, which is why barometers are useful for tracking atmospheric pressure changes and predicting weather conditions.

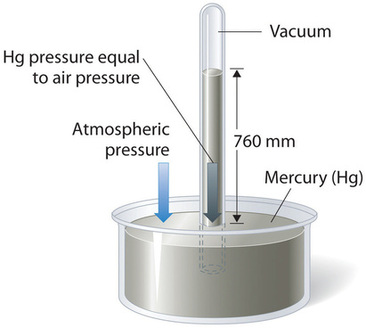
Figure $\PageIndex{2}$: A Mercury Barometer. The pressure exerted by the atmosphere on the surface of the pool of mercury supports a column of mercury in the tube that is about 760 mm tall.

Mercury barometers have been used to measure atmospheric pressure for centuries, leading to the development of a specific pressure unit: the millimeter of mercury (mmHg), also called the torr in honor of Torricelli. Standard atmospheric pressure is defined as the pressure required to support a 760 mm column of mercury in a barometer. This pressure is also known as 1 atmosphere (atm).

The atmosphere (atm) is commonly used in chemistry, but pressure can also be expressed in other units. The relationships between these units are:

\[
\begin{align*}
\rm 1\; atm &= 760 \; mmHg \\[4pt]
            &= 760 \; torr \\[4pt]
            &= 1.01325 \times 10^5 \; Pa \\[4pt]
            &= 101.325 \; kPa
\end{align*}
\]

Thus, a pressure of 1 atm is exactly 760 mmHg.

We rarely notice the absolute value of atmospheric pressure because we are constantly surrounded by it. However, we do feel changes in pressure, such as when our ears pop during rapid changes in altitude—like when riding a fast elevator, flying in an airplane, or driving through mountains. These pressure shifts cause the air inside our ears to adjust, making us more aware of the surrounding pressure.

Example $\PageIndex{1}$: Conversion of Pressure Units

A typical pressure in Toronto is 1.01 atm. What is this pressure in millimeters of mercury?

Solution

This is a unit conversion problem. 1 atm = 760 mmHg

$$
1.01 \mathrm{~atm}\left(\frac{760 \mathrm{mmHg}}{1 \mathrm{~atm}}\right)=768 \mathrm{mmHg} \nonumber
$$

Exercise $\PageIndex{1}$: Pressure Units

Mt. Logan, at 5959 m above sea level, is Canada’s tallest mountain. The normal barometric pressure at this altitude is about 360 mmHg. Convert this pressure to atm.

Answer: 0.47 atm

Manometers

A manometer is a device used to measure the pressure of a gas trapped in a container. It works similarly to a barometer but is specifically designed to measure the pressure of a gas sample. The key component of a manometer is a U-shaped tube containing mercury (or another nonvolatile liquid).

There are two types of manometers: closed-end and open-end.

A closed-end manometer, shown in Figure $\PageIndex{3}$a, has one end of the U-tube sealed. When no gas is present in the bulb, the heights of the mercury columns in both arms are equal because the space above the mercury in the sealed arm is a vacuum (containing only traces of mercury vapor). When a gas is introduced into the bulb, it exerts pressure on the mercury in the right column, causing the two columns to have different heights. The difference in height directly represents the pressure of the gas in the bulb.

Figure $\PageIndex{3}$: The Two Types of Manometer. (a) In a closed-end manometer, the space above the mercury column on the left (the reference arm) is essentially a vacuum (P ≈ 0), and the difference in the heights of the two columns gives the pressure of the gas in the bulb directly. (b) In an open-end manometer, the left (reference) arm is open to the atmosphere (P ≈ 1 atm), and the difference in the heights of the two columns gives the *difference* between atmospheric pressure and the pressure of the gas in the bulb.

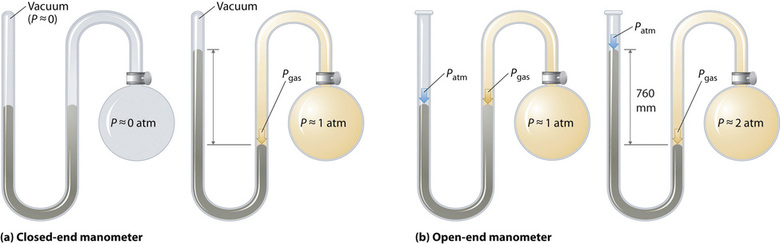
An open-end manometer, shown in Figure $\PageIndex{3}$b, has one end of the U-tube open to the atmosphere. The behavior of the mercury column depends on the relationship between the gas pressure in the bulb and atmospheric pressure:

If the gas pressure inside the bulb is equal to atmospheric pressure, the mercury levels in both arms will be the same.
If the gas pressure inside the bulb is greater than atmospheric pressure, the gas pushes the mercury down in the arm connected to the bulb, raising the mercury level in the open arm. The gas pressure is calculated as atmospheric pressure plus the height difference between the two mercury levels.
If the gas pressure inside the bulb is lower than atmospheric pressure, the mercury level in the bulb-connected arm will be higher than in the open arm. In this case, the gas pressure is calculated as atmospheric pressure minus the height difference.

Example $\PageIndex{2}$: Calculation of Pressure Using an Open-End Manometer

The pressure of a sample of gas is measured at sea level with an open-end Hg (mercury) manometer, as shown below. Atmospheric pressure is 760 mmHg. Determine the pressure of the gas in mmHg and atm.

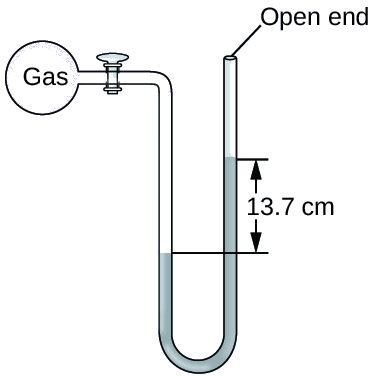
Ex9.1.3.png — The height is the difference between the two levels of mercury on each side of the U tube and has a value of 13.7 centimeters. The level on the right side is higher than on the left.

Solution

The pressure of the gas equals the pressure due to a column of mercury of height 13.7 cm plus the pressure of the atmosphere at sea level.

Convert 13.7 cm to mm.

$$
13.7 \mathrm{cm}\left(\frac{10 \mathrm{~mm}}{\mathrm{cm}}\right)=137 \mathrm{~mm} \nonumber
$$

Since the level of the mercury is lower at the gas side of the U-tube, the gas pressure is greater than atmospheric pressure.

P_gas = 137 mmHg + 760 mmHg = 897 mmHg.

$\mathrm{897\cancel{mm Hg}×\dfrac{1\: atm}{760\cancel{mm Hg}}=1.18\: atm}$

Exercise $\PageIndex{2}$

The pressure of a sample of gas is measured at sea level with an open-end Hg manometer, as shown below. Determine the pressure of the gas in mmHg and atm.

The height is the difference between the two levels of mercury on each side of the U tube and has a value of 11.76 cm. The level on the left side is higher than the right.

Answer: 642 mmHg, 0.845 atm

Chemistry in Everyday Life: Measuring Blood Pressure

Blood pressure is measured using a sphygmomanometer, a device that consists of an inflatable cuff, a manometer to measure pressure, and a method to detect blood flow. Invented in 1881, it remains a vital medical tool for assessing cardiovascular health (Figure (\PageIndex{4})).

To measure blood pressure, the cuff is wrapped around the upper arm and inflated until it temporarily stops blood flow. As the cuff slowly deflates, blood begins to flow again, and two key pressure measurements are recorded.

The systolic pressure is the highest pressure in the arteries, occurring when the heart beats and pushes blood through the circulatory system. When the cuff’s pressure drops to match the systolic pressure, blood starts flowing past the cuff, producing sounds that can be heard through a stethoscope. This is the first reading on the gauge.

The diastolic pressure is the lowest pressure, occurring when the heart is at rest between beats. As the cuff deflates further, blood flow returns to normal, and the sound of pulsing blood fades. The pressure at this moment represents the diastolic pressure, which is recorded as the second reading.

Blood pressure is expressed in millimeters of mercury (mmHg), reflecting the historical use of mercury-based manometers in medical instruments. A typical healthy blood pressure reading is 120/80 mmHg, where 120 mmHg is the systolic pressure and 80 mmHg is the diastolic pressure.

Figure $\PageIndex{4}$: (a) A medical technician prepares to measure a patient’s blood pressure with a sphygmomanometer. (b) A typical sphygmomanometer uses a valved rubber bulb to inflate the cuff and a gauge to measure pressure. (credit a: modification of work by Master Sgt. Jeffrey Allen)

Summary

A complete description of a gas sample requires four measurable quantities: temperature, volume, amount, and pressure. Pressure is defined as force per unit area, with the SI unit being the pascal (Pa), where 1 Pa = 1 N/m². The pressure exerted by an object is proportional to the force it applies and inversely proportional to the area on which the force is distributed.

The pressure exerted by Earth’s atmosphere, known as atmospheric pressure, is approximately 101 kPa (1 atm) at sea level. It is commonly measured using a barometer, a closed, inverted mercury-filled tube, where the height of the mercury column corresponds to atmospheric pressure. This pressure is often reported in millimeters of mercury (mmHg), also called torr.

A manometer is used to measure the pressure of a gas sample. A closed-end manometer directly measures gas pressure relative to a vacuum, while an open-end manometer compares gas pressure to atmospheric pressure, adjusting for differences in column height.

Search

Text Color

Text Size

Margin Size

Font Type

Example \(\PageIndex{1}\): Conversion of Pressure Units

Solution

Exercise \(\PageIndex{1}\): Pressure Units

Example \(\PageIndex{2}\): Calculation of Pressure Using an Open-End Manometer

Solution

Exercise \(\PageIndex{2}\)

Chemistry in Everyday Life: Measuring Blood Pressure