18.2: Dispersal of Energy- Entropy

Introduction

To understand the direction of spontaneity we need to introduce the concept of entropy and the Second Law of Thermodynamics, which states that for a spontaneous process the entropy of the universe increases. There are two definitions for entropy, the first is the thermodynamic definition developed by Clausius and is the operational definition we will be using in this class.

\[S=\frac{q_{reversible}}{T_{absolute}}\]

This definition is based on the work of Carnot, who studied steam heat engines and their efficiency as energy was transferred from the high temperature to the low temperature reservoirs.

Figure\(\PageIndex{1}\): Nicholas Léonard Sadi Carnot’s research into steam-powered machinery and (b) Rudolf Clausius’s later study of those findings led to groundbreaking discoveries about spontaneous heat flow processes.

The second definition is often called the configurational or statistical definition, as it is based on statistical thermodynamics and the ways a system can be configured.

\[ S= K_{B}\ln W \]

Where K_B is the Boltzmann's constant (1.38065 × 10⁻²³ J/K) and W (often labeled \(\Omega\)) is the number of possible arrangements of the system. Boltzmann's work was actually on gases and K_B is the ideal gas constant (R) divided by Avogadro's number. Boltzmann's constant are now one of the "immutable" fundamental constants that is being used for the redefined SI base units.

Figure\(\PageIndex{2}\): The Boltzmann equation is engraved on Ludwig Boltzmann's gravestone.

In this view, there are "microstates" that describe the various ways energy and matter can be configured, and the observable macroscopic state is a result of the probability of the available microstates. This will be briefly developed in the next section (18.3), with a focus on conceptual understanding.

Entropy is a State Function

Entropy is a state function like enthalpy or internal energy (review Section 5.4.4). This can be seen by rearranging Clausius's eq. for entropy as follows:

\[\Delta S =\frac{q_{rev}}{T} \rightarrow q_{rev}=T\Delta S \\ noting \; \; \Delta H = q_{rev,p} \; \; gives \\ \Delta H =T\Delta S\]

This means that like enthalpy, the entropy change between the final and initial state is independent of the path and only dependent of the values of the final and initial states.

Entropy as an Extensive Property

Extensive properties depend on the extent of the system (review section 1.6 Physical Properties) and properties like enthalpy, volume and mass are extensive (2 gallons of gasoline have twice the volume, mass and energy than one gallon), while intensive properties do not depend on the extent of the system (combining two one gallon containers of water at 25^oC does not result in two gallons at 50^oC, but two gallons at 25^oC).

If we take a closer look

\[\Delta H =T\Delta S\]

Since Enthalpy is an extensive property, and temperature is an intensive property, entropy must be extensive.

Second Law of Thermodynamics

The Second Law of Thermodynamics states that for a spontaneous process, the entropy of the Universe increases. This is often called times arrow, and the challenge is, how do we measure an increase in the entropy of the universe?

\[\Delta S_{Universe}>0\]

But also, as we shall see, the second law allows us to determine if a system is at equilibrium, and if it is not, in which way it will proceed (as it proceeds in the direction defined by the second law).

Third Law of Thermodynamics

The third law of thermodynamics states that the entropy of a pure crystal at the temperature of absolute zero is zero. A pure crystal is a crystal with a mono-isotopic constitution where there is only one possible microstate that represents its arrangement. If there was another isotope that would introduce entropy as there would be more than one microstate that could represent where the different isotopes are located.

At any temperature above absolute zero, the particle (atoms, molecules, or ions) that compose a chemical system can undergo several types of molecular motion, including translation, rotation, and vibration (Figure \(\PageIndex{1}\)). The greater the molecular motion of a system, the greater the number of possible microstates and the higher the entropy. A perfectly ordered system with only a single microstate available to it would have an entropy of zero. The only system that meets this criterion is a perfect crystal at a temperature of absolute zero (0 K), where each component atom, molecule, or ion is identical and fixed in place within a crystal lattice and exhibits no motion (ignoring quantum effects). Such a state of perfect order (or, conversely, zero disorder) corresponds to zero entropy. In practice, absolute zero is an ideal temperature that is unobtainable, and a perfect single crystal is also an ideal that cannot be achieved. Nonetheless, the combination of these two ideals constitutes the basis for the third law of thermodynamics: the entropy of any perfectly ordered, crystalline substance at absolute zero is zero.

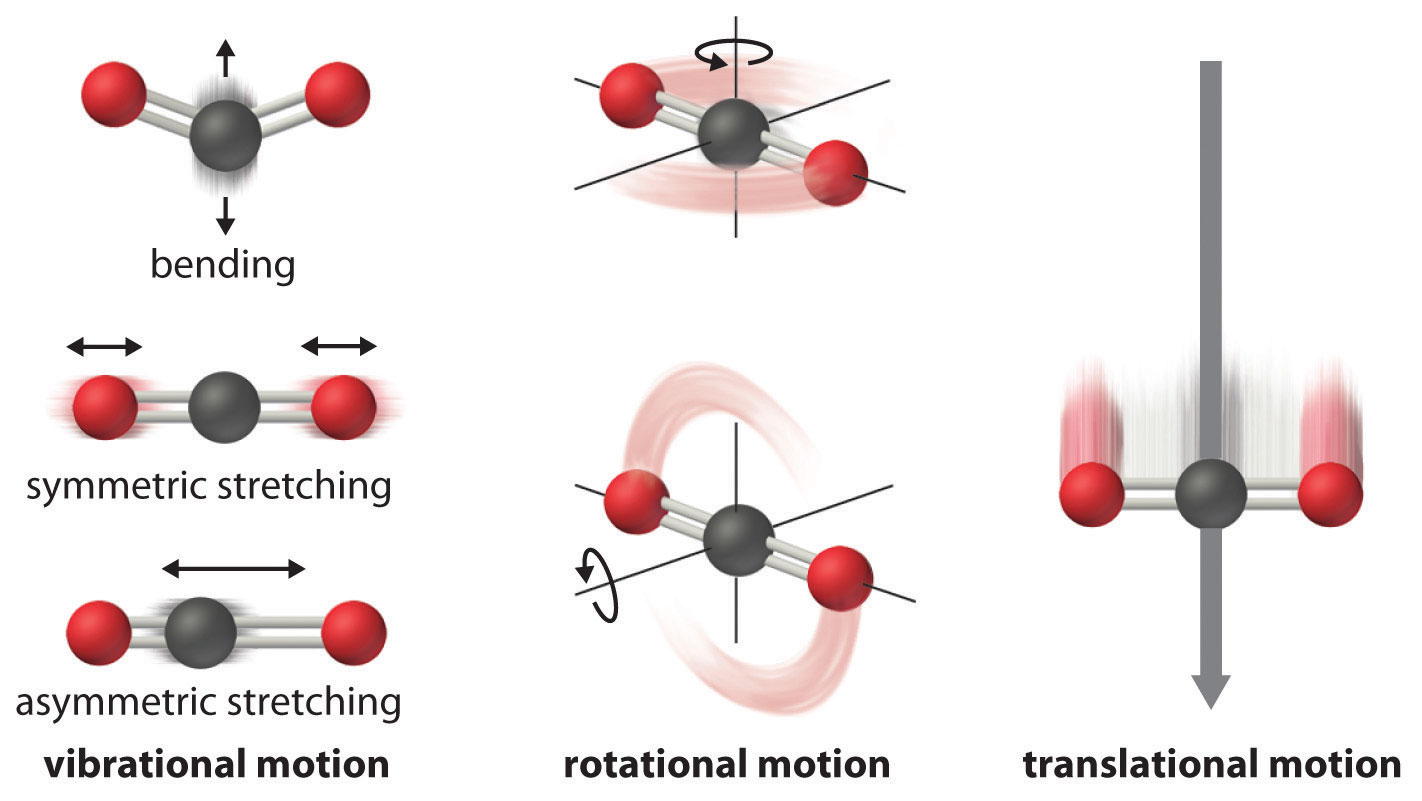
Figure \(\PageIndex{1}\): Molecular Motions. Vibrational, rotational, and translational motions of a carbon dioxide molecule are illustrated here. Only a perfectly ordered, crystalline substance at absolute zero would exhibit no molecular motion and have zero entropy. In practice, this is an unattainable ideal.

The third law of thermodynamics has two important consequences: it defines the sign of the entropy of any substance at temperatures above absolute zero as positive, and it provides a fixed reference point that allows us to measure the absolute entropy of any substance at any temperature. In practice, chemists determine the absolute entropy of a substance by measuring the molar heat capacity (C_p) as a function of temperature and then plotting the quantity C_p/T versus T. The area under the curve between 0 K and any temperature T is the absolute entropy of the substance at T. In contrast, other thermodynamic properties, such as internal energy and enthalpy, can be evaluated in only relative terms, not absolute terms. In this section, we examine two different ways to calculate ΔS for a reaction or a physical change. The first, based on the definition of absolute entropy provided by the third law of thermodynamics, uses tabulated values of absolute entropies of substances. The second, based on the fact that entropy is a state function, uses a thermodynamic cycle similar to those discussed previously.

Contributors and Attributions

Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, [e-mail]. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to: