18.1: Spontaneity and Energy Transfer
- Page ID
- 60788
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
This chapter builds upon chapter 5, Energy in Chemical Reactions, where we introduced two state functions, internal energy (U) and enthalpy (H), along with the First Law of Thermodynamics, which states that the energy change of the universe during a chemical process is zero. This allowed us to recognize that some reactions are exothermic and give heat to the surrounding, while others are endothermic and absorb heat from the surrounding. But it does not tell us if something will proceed spontaneously, and if so, in which directions and for how far? That is, in what direction will a chemical reaction proceed, and once completed, what will the equilibrium state look like? To answer these questions we will introduce in this chapter two new state functions, entropy (S) and Gibbs Free Energy (G), along with the second and third laws of thermodynamics. At the completion of this chapter you will be able to use thermodynamics to determine if a system is at equilibrium (Q=K), if it is product loaded (Q>K) or reactant loaded (Q<K), and what the composition of the system will look like when the reaction is over (K=?). That is, thermodynamics tells of if once the reaction is over you have lots of products (K>>1), lots of reactants (K<<1) or reactants and products coexisting in equilibrium (0.001<K<1000).
Thermodynamic Stability
Thermodynamics provides information on equilibrium conditions, but not how fast a state reaches equilibrium. This is important to understand as there are two different factors that influence the stability of a state, kinetics and thermodynamics. Consider the conversion of diamond to graphite. From the phase diagram of carbon, it can be seen that diamond is the thermodynamically favored allotrope under geological conditions of high pressure, but at ambient conditions, graphite is the more stable allotrope, and diamond spontaneously converts to graphite. Yet, diamonds are "stable" and this is because the activation energy for the process is so high that the rate becomes negligible, and to mortals, "diamonds last forever". The phase diagram is using the term "metastable diamond" to indicate that it is thermodynamically unstable, but kinetically stable, in the sense that the reaction rate is so slow that it is not observable on a normal timescale.
\[\ce{C}_{(s,\textrm{ diamond})}⟶\ce{C}_{(s,\textrm{ graphite})} \label{Eq1}\]
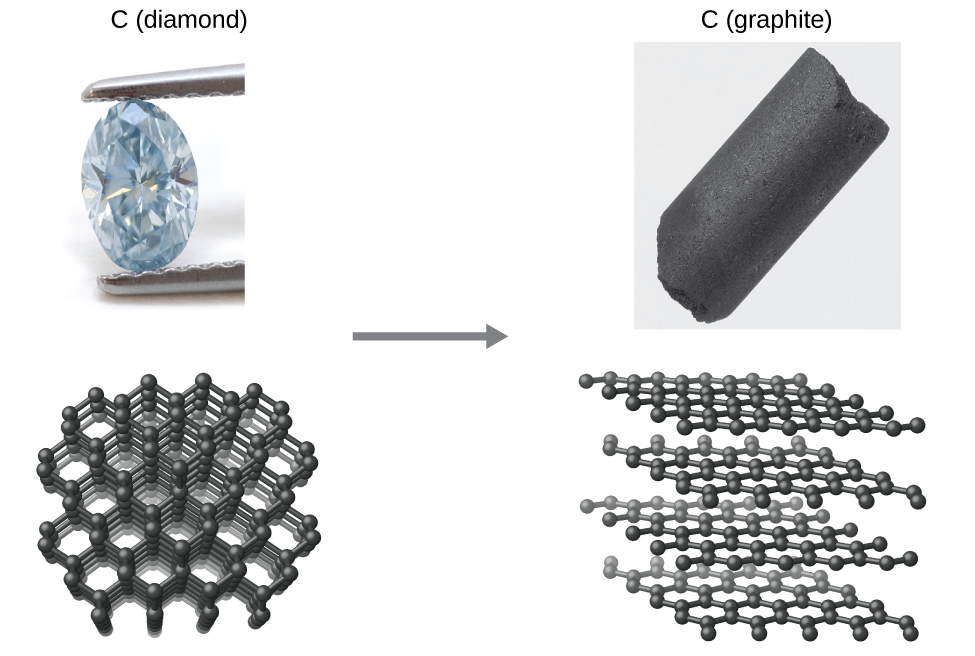 |
Figure\(\PageIndex{1}\): Phase diagram showing graphite is the stable form of carbon at ambient conditions (note 1 GPa = 9,869 atm, and 1 atm = 0.000101 GPa). This indicates diamonds are not stable at atmospheric conditions, but "Diamonds Last Forever", right? Diamond is called "metastable" because it requires such a high activation energy that the rate is so slow that it does not occur at an observable rate, but it is thermodynamically unstable. It is important to understand that thermodynamics does not tell you how fast a reaction happens, but if a system is at equilibrium, and if not, in what direction it will go to reach equilibrium.
So it is important in the study of chemistry to realize that thermodynamic state functions give us information on the stability and reactivity of a system from the perspective of the current state of a system as it transforms to the final equilibrium state, but not the kinetics on how the transition between states is achieved. In this chapter we will focus on the thermodynamic meaning of spontaneous, which is a process that occurs without being driven by the addition of an external energy source.
Spontaneous and Nonspontaneous Processes
From a thermodynamic perspective many spontaneous processes are exothermic and release energy, like a ball rolling down a hill or a piece of paper combusting into carbon dioxide and water. This implies a reverse process in a nonspontaneous direction where you must add energy to the system to make a process occur, like pushing the ball up the hill, or forming plant matter from carbon dioxide and water through photosynthesis, which uses the energy of the sun to drive the process. This model is correct in the sense that there is a direction of spontaneity, and thus a direction of nonspontaneity, but it is incorrect in the sense that spontaneity is not necessarily related to exothermicity (release of energy). Yes, exothermic reactions tend to be spontaneous, but some endothermic reactions are also spontaneous. Consider the freezing of water or the melting of ice, which process is spontaneous?
Figure\(\PageIndex{2}\): Does the ice melt or the water freeze? (image uploaded with permission of author).
Does the ice spontaneously melt (exothermic process) or the water spontaneously freeze (endothermic process)? Common sense tells us that it depends on the temperature; if the ambient temperature is above the freezing point the spontaneous process is the endothermic process of melting, while if the ambient temperature is below the freezing point it is the spontaneous exothermic process of freezing. So the direction of spontaneity is influenced by the temperature and can not be described by enthalpy and exothermicity alone. As we shall see, a new thermodynamic function called entropy can answer this question.
Dispersal of Matter and Energy
Expansion of Gas into Vacuum
Another spontaneous process is diffusion of a mobile substance from a region of high concentration to a region of lower concentration. Consider a gas in the left bulb of a container as in figure 18.1.3, where the right bulb is evacuated and contains no particles (Pright = 0, it is in a vacuum). If you open the stopcock the gas spontaneously flows from the left bulb to the right until the density is equal. Once this state is reached, the reverse process will not occur, where the gas completely leaves one bulb forming a vacuum.

Figure\(\PageIndex{3}\) The process of filling an evacuated container is spontaneous, while the reverse process of creating one is nonspontaneous.
If the above process occurs in an isolated system where no heat is transferred with the surroundings, the initial energy change of the right side is zero because P=0 (it is in a vacuum) and since the work of expansion is \(-P \Delta V\), (review 5.4.1) there is no initial reduction in energy and so the process of a gas expanding into a vacuum is not being driven by a lowering of energy, and indeed is being driven by the dispersal of matter. That is, the equilibrium state is the state where the matter is the most dispersed. This is not to say the number of particles in the two bulbs are the same, as one bulb may be larger than the other. This is saying they move from an area of high density to low density until the density is the same.
Thermal Heat Transfer
If we look at heat transfer (figure 18.1.4) we see a similar process to that of figure 18.1.3 except that energy in the form of heat is being dispersed, as energy is flowing from the hot object to the cold object. This does not mean the energy is flowing from the object with more energy to the object with less, as the cold object could be of greater mass, or be of a different type of material with a different heat capacitance (review section 5.2 heat capacitance, \(q=mc \Delta T\) . Initially the rate of heat transfer from the hot object to the cold object is faster than from the cold to the hot, and so there is a net transfer of heat from hot to cold until they reach the same temperature, at which time the rate of heat transfer between them is equal.

Figure\(\PageIndex{4}\): Transfer of heat energy from high to low temperature.
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:


