5.4: First Law of Thermodynamics
- Page ID
- 52109
Learning Objectives
- Determine how heat and work are related to the overall internal energy of a system
- Calculate the work done by/on a system at constant pressure (PV work)
- Calculate changes in internal energy and enthalpy using the First Law of Thermodynamics
- Define a state function and determine which variables are state functions
Introduction
In the very first Chapter of this book we described three attributes of matter.
- Matter has Mass
- Matter has Volume
- Matter has Energy
Thermodynamics comes from the Greek words therme (heat) and dynamis (power) and deals with the third attribute of matter, energy. In section 5.1.2 we defined energy as the capacity to do work or transfer heat. The first law of thermodynamics states that energy can not be created or destroyed, that is, the energy of the universe is constant. This allows us to define a thermodynamic system, which in the case of chemistry is a reaction, with the surroundings being everything else.
So what do we mean the reaction is a thermodynamic system? Lets consider the combustion of hydrogen
\[\ce{2H2 + O2 -> 2H2O}\]
During a chemical reaction the energy of the system changes as bonds in reactants are broken and the atoms rearrange to form the new bonds of the products. These new bonds are typically higher or lower in energy. If the products store more energy in their bonds, that energy must come from somewhere, and so it is transferred into the system from the surroundings. In the case of combustion, the products are lower in energy and so that energy is transferred to the surroundings. The key point here is as a reaction proceeds energy flows into or out of the system, depending on whether energy is absorbed or released as the products are formed. So what is positive energy flow?
Convention for Energy Flow
The convention thermodynamics use is that positive energy is when the system gains energy, which is when either heat is transferred to, or work is done on the system. This requires differentiating the system from the surroundings. In chemical thermodynamics, the system represents the internal energy of the atoms of the reactants as they become products.
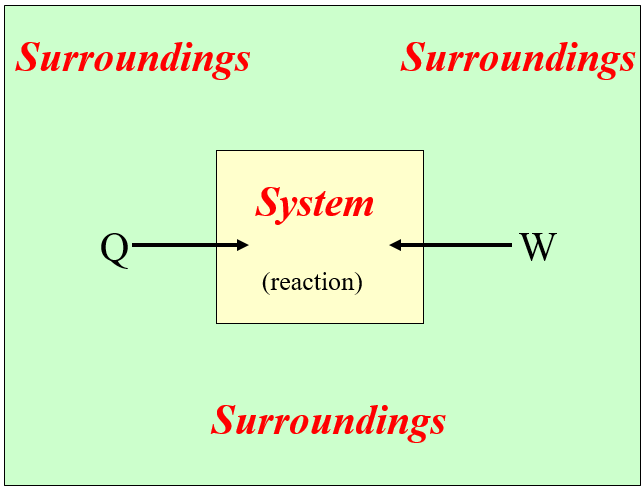
- Positive Energy Flow is when heat is added and/or work done to the system. (the system gains energy)
- \(\Delta E_{reaction}\) > 0
- Negative Energy Flow is when the system releases work to the surroundings and/or does work on the surroundings. (the system looses energy).
- \(\Delta E_{reaction}\) < 0
From the perspective of a thermodynamic system we can view the universe to consist of the system and the surroundings
\[Universe=System+Surroundings\]
The first law states that the energy of the universe is a constant and so the change in the energy of the universe must equal zero.
\[\Delta E_{Universe} = 0\]
Since the Universe is the system and the surrounding this means the change in energy of the system and surrounding must also equal zero
\[\Delta E_{Universe} = \Delta E_{System} + \Delta E_{Surrounding} = 0\]
therefore,
\[ \Delta E_{System} = - \Delta E_{Surrounding}\]
This is logical and means any energy lost by the system must be gained by the surroundings, and vice-versa, any energy gained by the system must be lost by the surroundings.
We define the energy of the system as the internal energy and give it the symbol U.
\[ \Delta U = - \Delta E_{Surrounding}\]
Note: Direction of Heat Transfer
Students often confuse heat and temperature. If two objects are in thermal contact with each other and are different temperatures, heat will transfer from the higher temperature object to the one at the lower. So the temperature difference defines the direction of heat transfer, but not the energy of the ojbects. To understand this we need to look at the Second Law of Thermodynamics and another state function called entropy, which is covered in the second semester class.
Exercise \(\PageIndex{1}\)
Does heat always flow from the object with more energy to the one with less?
- Answer
-
No, it transfers from the one with the higher temperature to the one at a lower temperature. A lake at 30oC has more energy than a cup of water at 35oC, but if you add the water to the lake, it will cool as energy flows from the water to the lake.
Enthalpy
Enthalpy (\(H\)) comes from the Greek enthalpein, meaning (“to warm”). which is the measure of the heat of a system. From above we know the change in internal energy (U) of a system is equal to the heat and work done on the system.
\[ΔU=Q+W \label{1st}\]
From section 5.1 we know the work of expansion is \(PV\) work, which for a system at constant pressure is
\[W=-PΔV \label{work}\]
Enthalpy \(ΔH\) is defined as the heat transferred at constant pressure \(Q_p\),
\[\Delta H=Q_p\label{heat}\]
substituting the definitions of work (Equation \ref{work}) and heat (Equation \ref{heat}) into Equation \ref{1st} at constant \(P\) gives,
\[ΔU= ΔH -PΔV\]
rearranging to solve for enthalpy gives:
\[ΔH = ΔU + PΔV \label{enthalpy}\]
a more general definition of enthalpy (which can be extended to conditions that are not at constant pressure is
\[H=U+PV\]
Note: relating enthalpy to work of expansion
In section 5.1.4 we introduced PV work as the work of expansion. That is, an expanding gas does work against the environment, and it takes work to compress a gas. According to the First Law, Positive work is when work is done on the system, which is that of compression, where \(\Delta\) V is negative. so -P\(\Delta\)V is positive work, and equation \ref{enthalpy} becomes
\[\Delta H = \Delta U - W\]
That is the enthalpy of a reaction is the heat transferred minus the work done on the system by a change in the volume of the system. That is, some of the energy change in going from reactants to products can be consumed by the system as it changes volumes, and this is most noticeable in gas phase systems.
Exercise \(\PageIndex{2}\)
Calculate the Enthalpy change for a gas phase reaction at 1.2 atm if the change in internal energy is 47kJ and the volume increase by 1.1 L to 41.0 L. Note 1L-atm =101.325J
- Answer
-
\[\Delta H=47kJ +1.2atm(41.0L-1.1L)\left ( \frac{101.325J}{L\cdot atm} \right )=52kJ\]
We often call enthalpy the Heat of Reaction and tabulate tables of enthalpies of reaction, which can be used to tabulate the heat given off during a reaction.
State Functions
Enthalpy and Internal Energy are state functions. A state function is a function whose value is defined by the state, its pressure, temperature, composition, and amount of substance, and not the process of how it was obtained. So the difference between two state functions is path independent. Thus any solution of NaCl at 25°C and 1 atm that contains a mixture of 1 mol NaCl and 100 mol H2O has the same internal energy and the same enthalpy as any other solution with the same specifications. It does not matter whether the solution was prepared by simply dissolving NaCl(s) in H2O, by reacting NaOH(aq) with HCl(aq), or by some other method.
Is work a state function? No, as work is path dependent. If you look at Figure \(\PageIndex{2}\) you have a nice analogy for understanding the state function. The gravitational potential energy difference between an object at a height of the summit of Mt. Kilimanjaro and it's base is the same, no matter how you made it to the summit. The green and red path "X" and "Y" represent different paths, and the work required does depend on the path.

Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Ronia Kattoum (UALR)
- anonymous


