9.2: Valence Bond Theory
- Page ID
- 52898
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Valence bond theory is an approach to bonding where molecular orbitals (wave functions) are considered to be the result of the mixing of pure atomic orbitals (section 6.6). These mixed or hybrid obritals are the orbitals used in VSEPR models of section 8.6 . The first period of the periodic table does not form hybrid orbitals because there is only one 1s orbital (to form a hybrid two or more things must mix). The second period can form up to four hybrid orbitals because there is one 2s orbital and three 2p orbitals and these are related to VESPR geometries of 2,3 and 4 electron domains. The third period (and higher) have d orbitals that can be involved in hybridization and so they can have expanded octets, and hybrid orbitals involving s,p and d orbitals result in 5 and 6 electron domain VSEPR geometries.
Hybrid Orbitals
These are the orbitals responsible for the VESPR geometries. There are five basic VESPR geometries and so there are five hybrid orbitals that we will look at, ranging from two to six electron domains. The name of the hybrid orbital indicates the number of atomic orbitals involved in the hybridization are outlined in table \(\PageIndex{1}\).
| Hybrid Orbital |
Number of Hybrid Orbitals |
Atomic Orbitals Mixed |
Hybrization Characterization |
VSEPR (electronic) Geometry |
Examples |
| sp | 2 | s,p | 1/2s, 1/2p | 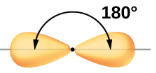 Linear |
BeH2, CO2 |
| sp2 | 3 | s,p,p | 1/3s, 2/3p | 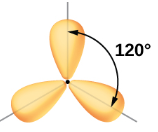 Trigonal Planar Trigonal Planar |
SO3, NO3-, AlCl3, SO2, O3 |
| sp3 | 4 | s,p,p,p | 1/4s, 3/4p |  Tetrahedral |
CH4, NH3, H2O |
| sp3d | 5 | s,p,p,p,d | 1/5s, 3/5p, 1/5d | 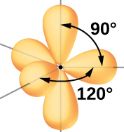 Trigonal Bipyramidal |
PF5, SeF4 |
| sp3d2 | 6 | s,p,p,p,d,d | 1/6s, 1/2p, 1/3d | 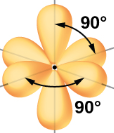 Octahedral Octahedral |
SF6, |
Note, second period elements have no d orbitals and so can not have more than an octet of electrons, that is, only the third period and greater can form sp3d and sp3d2
Requirements for Hybridization of Atomic Orbitals
- Atomic orbitals need to be in similar regions of space
- Atomic orbitals need to be of similar energy (a 1s will not hybridize with a 4p).
- Energy is conserved
- the two 2sp orbitals have an energy that is halfway between the 2s and 2p atomic orbitals.
- the three 2sp2 hybrid orbitals have an energy that is two thirds the distance between the 2p and 2s atomic orbitals (closer to the energy of the p).
- the four 2sp3 hybrid orbitals have an energy that is three fourths the distance between the 2p and 2s atomic orbitals (closer to the energy of the p).
- Number of hybrid orbitals created equals number of atomic orbitals mixed.
Bond Formation and \(\sigma\) bonds
One way of looking at the formation of a bond is for two atoms with a free radical atomic orbital (atomic orbital with one electron) to come together and overlap and form molecular orbitals. This is the opposite of homolytic bond cleavage that was discussed in section 8.9 . In this model, we consider two atoms to approach from infinity with one electron in an orbital of each atom, and when they overlap a covalent sigma bond is formed. This can be expressed by the potential well diagram that we have looked at throughout this semester
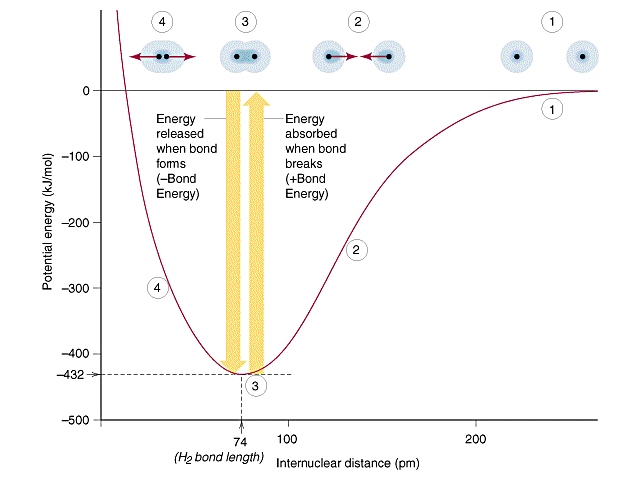
Now let's look at BeH2, which we know has two single bonds. In the ground state beryllium has an electron configuration of Be: [He]2s2, which means it does not have two orbitals with a single electron that could overlap with the single electron in hydrogen's orbital as occurs in Figure \(\PageIndex{1}\). Instead, what happens is the s orbital hybridizes with a p orbital and the two electrons in the 2s orbital are now shared by two orbitals, the two 2sp orbitals. Before proceeding watch video \(\PageIndex{1}\).
Video \(\PageIndex{1}\): 10'11" YouTube ukploaded by Van Wyk on molecular shapes and hybrid orbitals (https://youtu.be/qraDpWX_msY)
The Hybrid Orbitals
sp Hybrid
- Linear Geometry
- 180o bond angle
- molecules with sp hybrid orbitals may also be involved with \(\pi\) bonds (see section 9.2.4)
In Figure \(\PageIndex{2}\) we note that the p orbitals align along Cartesian axes, and so if we consider the s to hybridize with the px then the two sp orbitals face in opposite directions along the x-axis.

Let's follow through with beryllium hydride mentioned above. The beryllium in beryllium hydride (BeH2) is an example of an sp hybrid. If we look at the ground state electron configuration of Be, it is [He]1s2, and so it has a filled valence orbital and as such, could not bond. This is shown on the left electron configuration of Figure \(\PageIndex{3}\), where on the right, the two red arrows are the Be sp orbitals which are equal in energy (half way between the 2s and sp) and with one electron in each, can overlap with the 1s orbitals of two different hydrogen atoms.
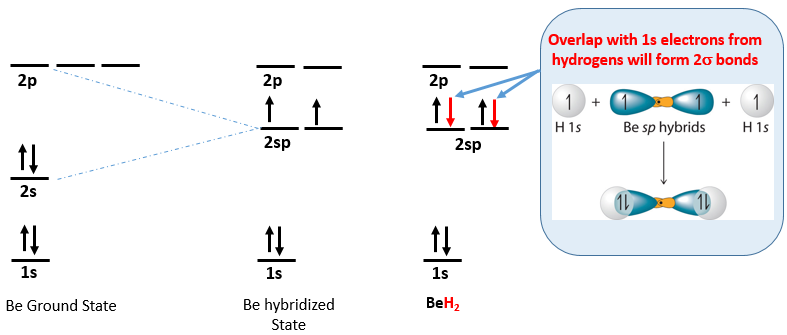
Figure \(\PageIndex{3}\): Electron configuration of beryllium (left), in hybridized state with two orbitals containing a lone electron (middle) and for beryllium hydride (right). The rightmost configuration is the linear molecule H-Be-H with and the right image is not showing the energy of the \(\sigma\) bond, but how it can be formed with the overlap of the H1s orbitals of two hydrogen atoms with the two Be hybrid 2sp orbitals.
Exercise \(\PageIndex{1}\)
What is the orbital of the chlorine in \(\ce{BeCl2}\)?
- Answer
-
it is a 3p orbital as chlorine has one free-radical orbital in it's valence state, and so there is no need to hybridize it.
sp2 hybrid
- Trigonal planar geometry
- 120o bond angle
- molecules with sp2 hybrid orbitals may also be involved with \(\pi\) bonds (see section 9.2.4)
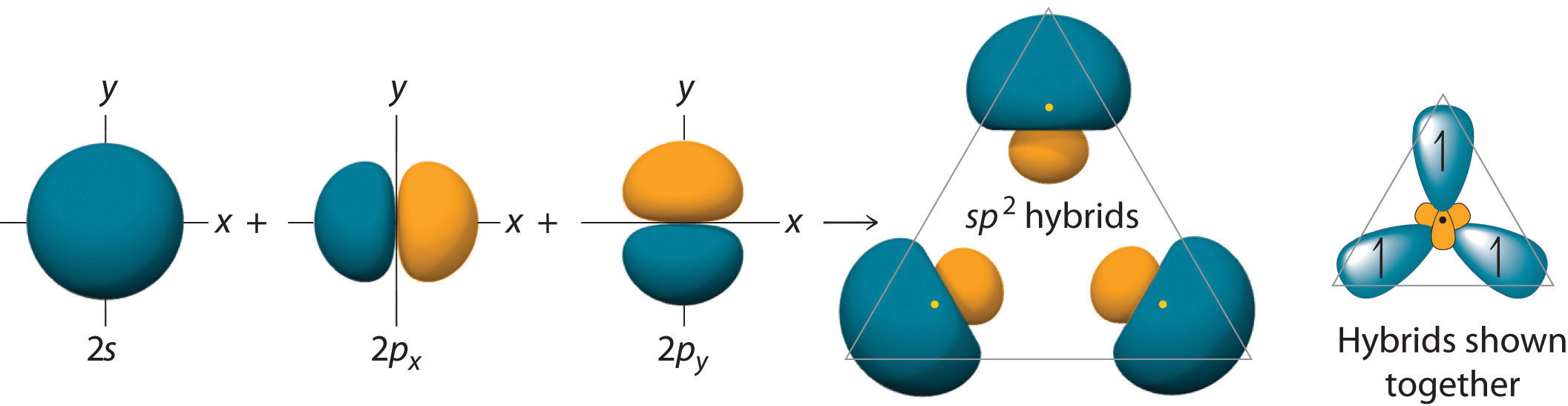
Figure \(\PageIndex{4}\): sp2 hybrids form a trigonal planar structure
Lets look at boron trihydride (BH3)
The ground state of boron is [He]2s22p1 and so can not account for the three bonds in boron trihydride, and the valence bond approach it to hybridize the 2s with two of the 2p orbitals giving three sp2 hybridized orbitals with one electron each, which can then bond with the lone electron in hydrogen's 1s orbital, as indicated in Figure \(\PageIndex{4}\). It should be noted that halogens form analogous structures like BFH3 where the bonding electron from the halogen comes from the p orbital with a lone electron.
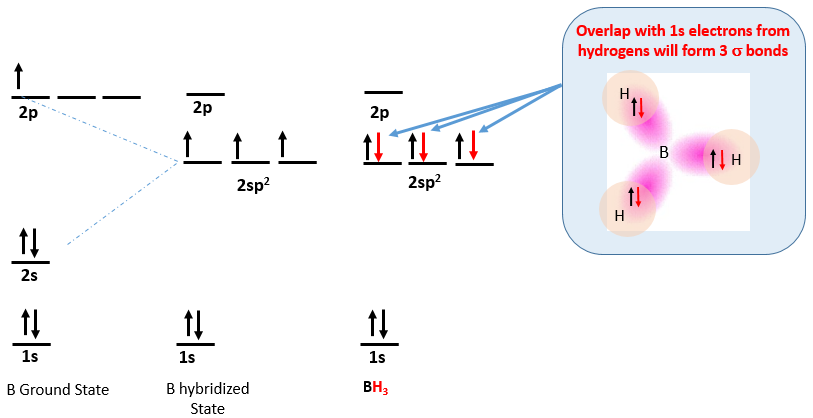
Figure \(\PageIndex{5}\): Boron can form three bonds when it has sp2 hybrid orbitals
Fluorine forms an analogous structure where the lone electron is in a 2p orbital
sp3 hybrid
- tetrahedral electronic geometry
- 109.5o bond angle
Molecules with 4 "electron domains" have sp3 hybridized orbitals. The four sp3 hybridized orbitals result from the mixing of 1 s orbital with 3 p orbitals orient in 3D space as they involve a px, py & pz and according to VSEPR orient in a tetrahedral structure as shown in Figure \(\PageIndex{9}\)

Figure \(\PageIndex{6}\): Tetrahedral structure of the four sp3 hybridized orbitals.
Methane (CH4) is from group IV and has 4 electrons in it's outer shell. This results in the following electron configuration and a tetrahedral molecule.
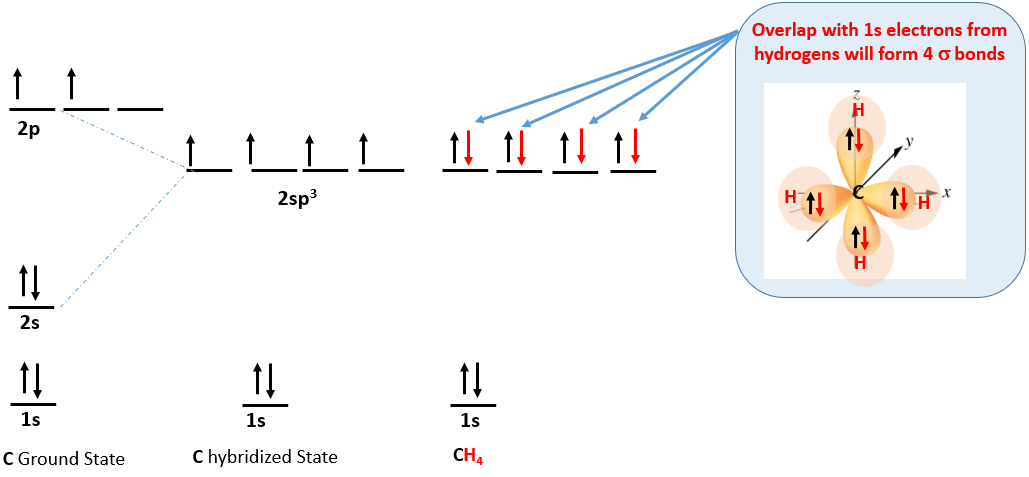
Figure \(\PageIndex{7}\): Hybridization of hydrogen-like atomic orbitals to produce sp3 hybrid orbitals responsible for tetrahedral VSEPR structure, with all orbitals being \(\sigma\) bonding orbitals. Note the energy of the hybrid is 3/4ths the difference between the one 2s orbital and the three 2p orbitals that hybridized.
Ammonia (NH3) is from group V and has 5 electrons in it's outer shell. This results in the following electron configuration and a trigonal pyramidal molecule.
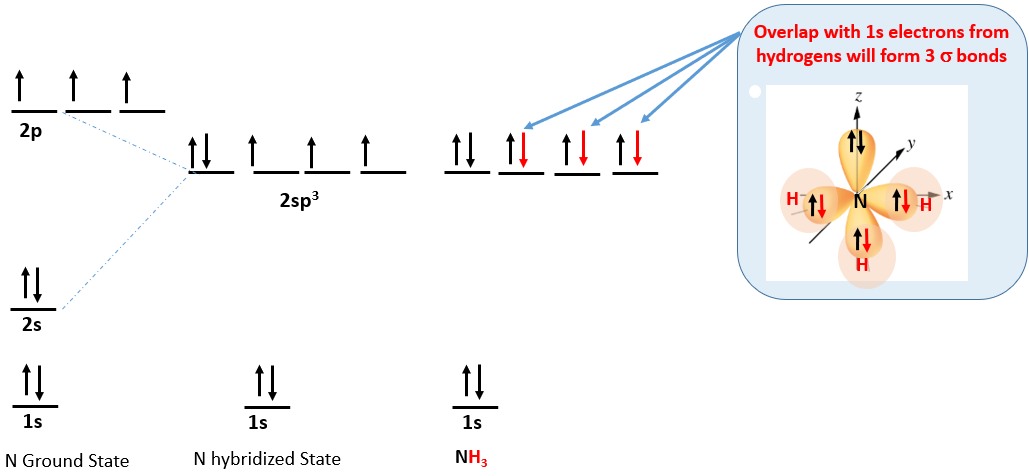
Figure \(\PageIndex{8}\): Ammonia has 5 electrons and so one of the hybrid orbitals has a lone pair, resulting in the trigonal pyramidal molecular geometry.
Water (H2O) is from group VI and has 6 electrons in it's outer shell. This results in the following electron configuration and a bent (104.5o) molecule.
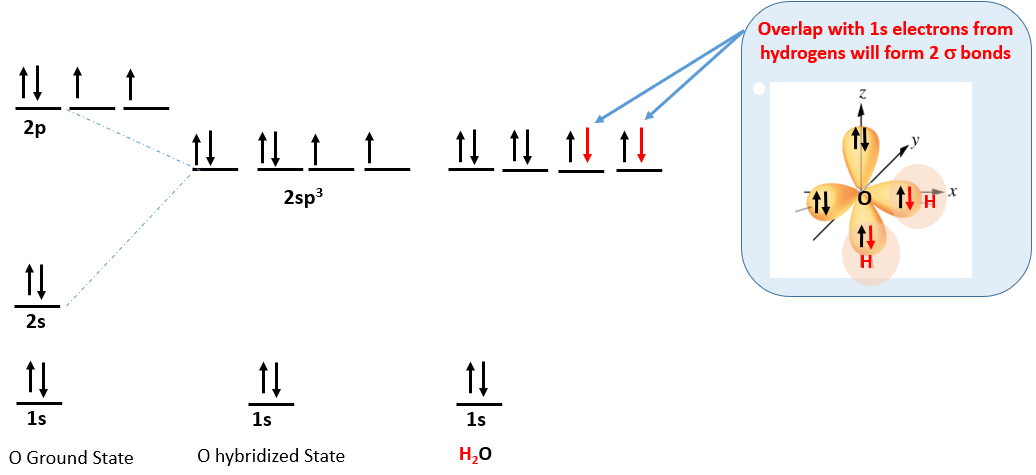
Figure \(\PageIndex{9}\): Water has six electrons and so two of the hybrid orbitals are filled (have lone pairs) and it forms a bent (104.5o) molecule.
sp3d hybrid
- trigonal bipyramidal electronic geometry
- 120o bond angle (equatorial-equatorial) and 90o bond angles (axial-equatorial)
Only elements in the third or greater period of the periodic table have d orbitals and so only those elements can have expanded octets.

Figure \(\PageIndex{10}\): The five atomic orbitals that combine to form the five sp3d hybrid obritals that result in a trigonal bipyramidal VSEPR structure
sp3d2 hybrid
- octahedral electronic geometry
- 90o bond angles
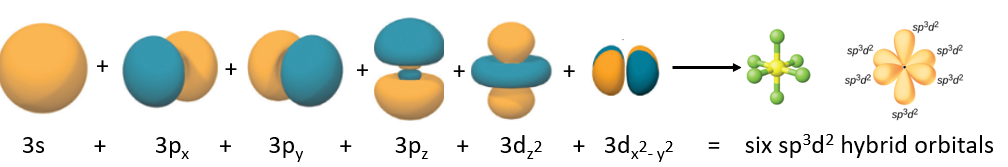
Figure \(\PageIndex{11}\): The six atomic orbitals that combine to form the six sp3d2 hybrid obritals that result in an octahedral VSEPR structure
\(\pi\) Bonds
So far we have described single \(\sigma\) bonds where the orbitals of two atoms overlap to form a bonding orbital with electron density along the internuclear axis, and these are responsible for the VSPER geometric structures. In this section we will describe a second type of bond, the \(\pi\) bond, which results from the overlap of adjacent unhybridized p orbitals. \(\pi\) bonds are weaker then \(\sigma bonds\) and have a node along the internuclear axis (actually a nodal plane), and thus \(\pi\) bonds have two regions of space where bonding occurs. If the \(\pi\) bond is formed by two pz orbitals on adjacent atoms there is electron density on both sides of the xy plane (which becomes a nodal plane). \(\pi\) bonds combine with \(\sigma\) bonds to form multiple bonds, with a double bond consisting of one \(\sigma\) and one \(\pi\)) bond, and a triple bond consisting of one \(\sigma\) and two \(\pi\) bonds. Video \(\PageIndex{2}\) illustrates a \(\pi\) bond.s
Double Bonds
A double bond consists of a \(\sigma\) and a \(\pi\) bond and these are common with adjacent atoms that have sp2 hybrid orbitals. Lets look at the C=C bond of ethylene C2H4. Figure \(\PageIndex{12}\) shows the electron configuration the carbon atoms would be in after hybridization where two of the p orbitals (px and py in this case) hybridize with the s to form the trigonal planar geometry defined by the three \(\sigma\) bonds (two to hydrogens and one to the second carbon). The fourth valence electron of carbon resides in the unhybridized p orbital (red electron) and if both of the carbons have their trigonal \(\sigma\) structures in the same plane, the two pz orbitals can overlap, as illustrated in Figure \(\PageIndex{12}\).
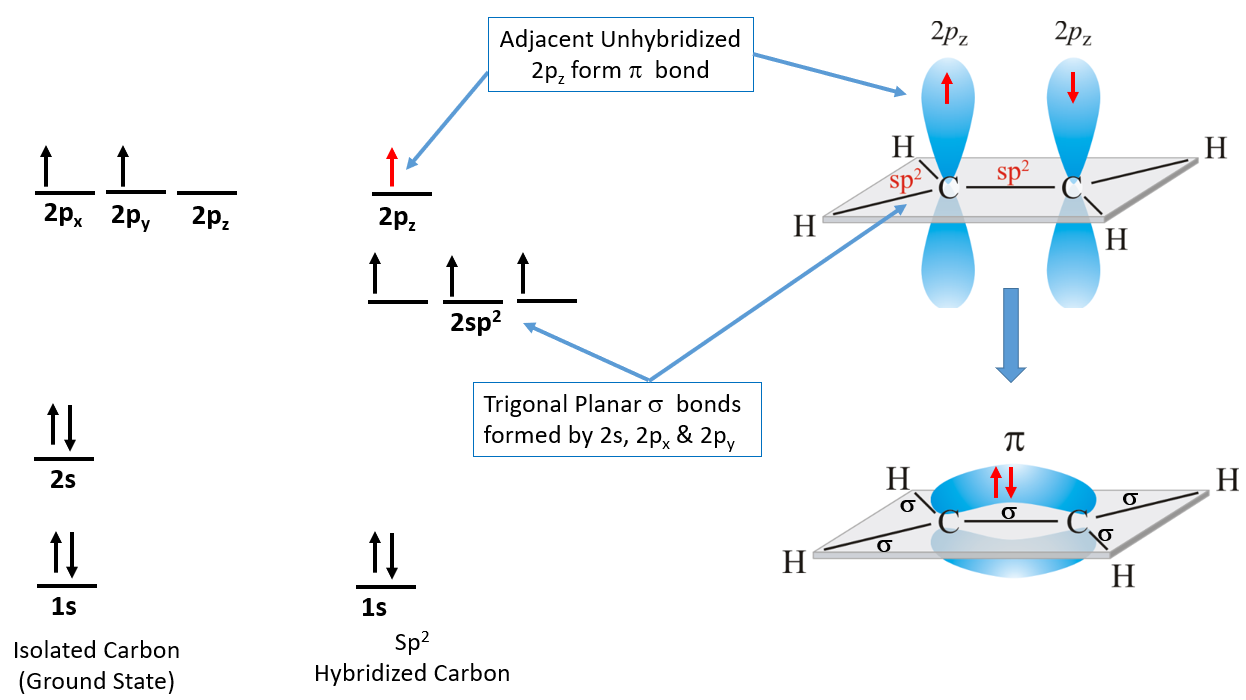
Figure \(\PageIndex{12}\): (modified image from: Eni Generalic, Chemistry Glossary)
There are several things to note about \(\pi\) bonds in double bonds.
- The sp2 framework of the sigma bonds must be in the same plane (ethylene is a planar molecule) and if you rotate one of the carbons 90o along the C-C axis, you break the pi bond.
- For there to be efficient orbital overlap of the unhybridized p orbitals the nuclei of the atoms need to be close to each other. This occurs for atoms of the second period and nitrogen, carbon and nitrogen can form \(\pi\) bonds. Silicon, unlike carbon, does not form stable double bonds because it is a larger atom and there is insufficient overlap of the p orbitals responsible for \(\pi\) bonds.
- \(\pi\) bonds prevent rotation. This is very important in biological systems as molecules freely rotate around single \(\sigma\) bonds but can not rotate around multiple bonds, which thus gives the molecule a fixed structure.
Resonance structures.
If more than two adjacent atoms have sp2 hybrid orbitals and they are all in a plane, the p orbitals of multiple atoms can overlap resulting in a \(\pi\) bond that extends across multiple atoms and this can not be drawn with a single Lewis dot structure, which is why we need resonance structures. Benzene (C6H6) is an example where the electrons in the \(\pi\) orbital are extended over 6 carbon atoms

Figure \(\PageIndex{13}\): Benzene has a \(\pi\) ring system delocalized over 6 carbon atoms (images [c] & [d] obtained from wikimedia commons and were uploaded by Zlir'a)
That above image gives a good bearing on some of the issues associated with Lewis dot structures. (a) and (b) are the Lewis resonance structures, and these do not indicate that the electrons in the second (\(\pi\) bond are delocalized over all the carbons. (c) shows the unhybridized p orbitals and (d) shows these overlaping above and below the plane the atoms and \(\sigma\) bonds exist in.
The following two YouTube animations give a feel for how \(\pi\) bonds can spread out over multiple atoms.
|
|
|
Triple Bond
In the triple bond there are two \(\pi\) bonds and one \(\sigma\) bond. These can occur when in acetylene (C2H2) where the carbon is sp hybridized leaving one electron in each of the two unhybridized p orbitals. This is shown in Figure \(\PageIndex{14}\) where each carbon forms two bonds, one with a hydrogen and one with the other carbon.
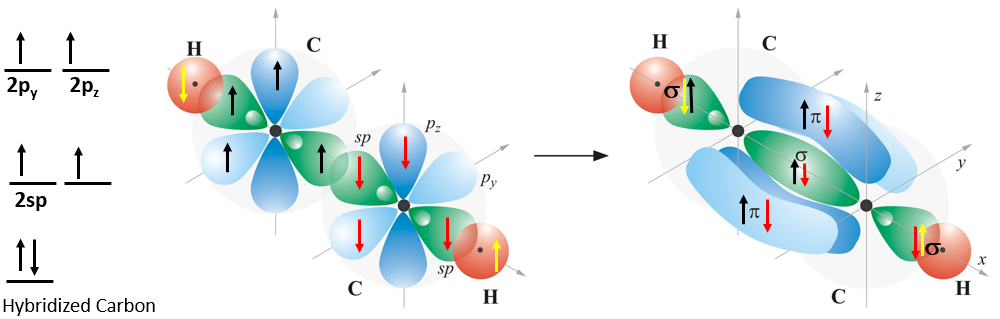
On the left is the electron configuration of the hybridized carbons, in the middle, these electrons are assigned with one of the carbon's electrons being in black, and the other in red. The hydrogen's are in yellow. Each carbon is sp hybridized and so the molecule is linear. The bond between the carbons is a triple bond because it hast one \(\sigma\) and two \(\pi\) bonds. Note each of the pi bonds has two lobes, above and below the plane defined by the axis of the other two p orbitals. That is, for the \(\pi\) bond formed from the overlap of pz orbitals, the xy plane is the nodal plane, with the \(\pi\) bond having no electron density along the internuclear axis. Video \(\PageIndex{5}\) illustrates the bonding in Figure \(\PageIndex{14}\).
Contributors and Attributions
- Narration: Bob Belford
- Images from LibreTexts of Stepen Lower, OpenStax


