9.3: Molecular Orbital Theory
- Page ID
- 52899
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
In valence bond (VB) theory we treat \(\sigma\) and \(\pi\) bonds as being the result of the overlap of atomic orbitals, that is, the bonding orbitals are the result of the overlap of the atomic orbitals of the bonding atoms. In molecular orbital (MO) theory we consider the orbitals to belong to the molecule, that is, the wavefunction is the quantum mechanical solution of the multinuclear molecule. Although MO calculations are beyond the scope this class we need to look at these for the simplest of molecules in order to understand the behavior of real molecules. For example, valence bond theory has no way of describing antibonding orbitals, which are very real and influence the behavior of molecules.
Chemists need both MO (Molecular Orbital) and VB (Valence Bond) theory. As we have seen in the last section, VB theory is very useful to predict the geometry of simple molecules based on the connectivity of atoms. It is easy to understand the concept of a bond as the overlap of half filled atomic orbitals between two different atoms, and VSPER correctly predicts the electronic geometry if there is more than one electron domain around an atom, which in turn allows the prediction of the molecular geometry. In this class we will tackle MO for the simplest of molecules, the diatomics, and use an easy to understand approach, LCAO-MO (Linear Combination of Atomic Orbital -Molecular Orbital). There are two types of diatomics, homonuclear like H2, Cl2 and and heteronuclear like HCl and HBr.
LCAO-MO Introduction
This describes molecular orbitals that are the result of the linear combination of atomic orbitals. A standing wave function ( \(\psi\)) has a [-] negative and a [+] region (which is not charge, see Figure \(\PageIndex{1}\)), which is why we used \(\psi^2\) to describe the probability of finding an electron in a region of space (review section 6.6 for atomic orbitals). If two waves interact and they have the same sign (positive or negative amplitude) they add to each other, and if they have opposite sign, they subtract from each other. It must be emphasized that the [+] and [-] does not represent charge, but describe the region of the wavefunction.

So in LCAO-MO of a diatomic, we look at the two wave functions, and how they can interact.
What are the factors involved with the mixing of atomic orbitals to produce a molecular orbital?
- The number of molecular orbitals equals the number of atomic orbitals that are mixed.
- The energies of the molecular orbitals equals the energies of the atomic orbitals that mixed them
- Bonding orbitals are lower in energy than the atomic orbitals
- Antibonding orbitals are higher in energy.
- The energies of the atomic orbitals must be near each other.
Molecular Orbitals involving s orbitals
Let's look at H2. There are two ways 1s orbitals can add to each other, constructively to form bonding orbitals or destructively to form antibonding orbitals (noting with an asterisk [*]). This type of interaction forms a \(\sigma\) bond because s orbitals can only overlap along an internuclear axis, and result in \(\sigma\) and \(\sigma^*\) orbitals (Figure \(\PageIndex{2}\)). Note, in these equations the wavefunctions of two 1 s orbitals \(\psi_{1s}\) combine to form a \(\psi_{\sigma_{1s}}\) and \(\psi_{\sigma^*_{1s}}\) orbitals and the \(\sigma_{1s}\) or \(\sigma^*_{1s}\) bond is the MO squared, \(\psi^2_{\sigma_{1s}}\) or \(\psi^2_{\sigma^*_{1s}}\)
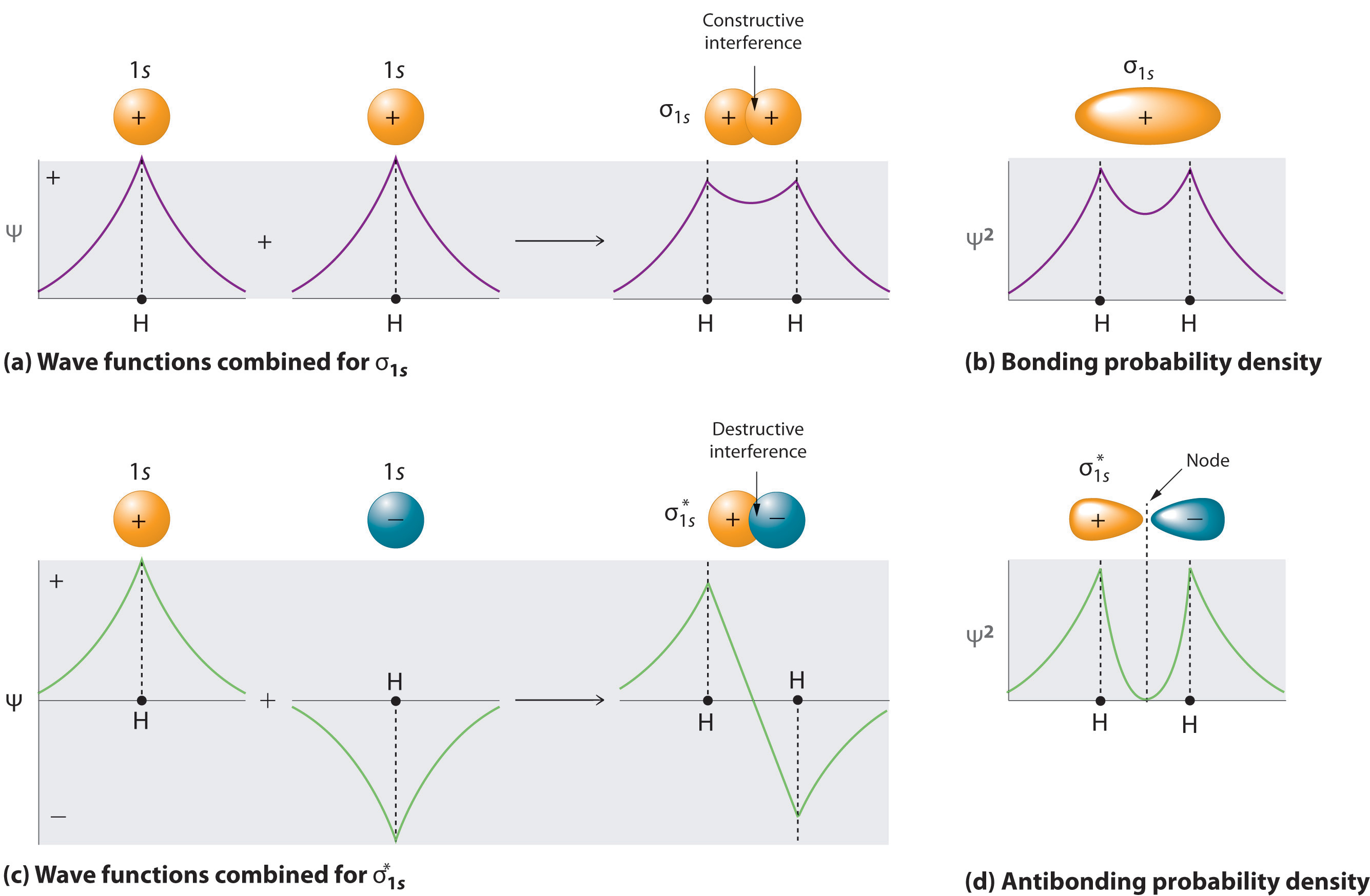
Figure \(\PageIndex{2}\): Constructive and destructive interferance of 1s orbitals that combine to form diatomic hydrogen.
Molecular Orbitals involving p orbitals
p orbitals can combine for form either \(\sigma\) bonds or \(\pi\), and these can be either bonding orbitals or antibonding orbitals. In the following images the z axis is considered to be the internuclear axis. Overlap of pz orbitals results in \(\sigma\) bonds and overlap of py or pz orbitals results in \(\pi\) bonds
\(\sigma_p\), \(\sigma_p^*\) orbitals
In the following images the color indicates the +/- regions of the wavefunction
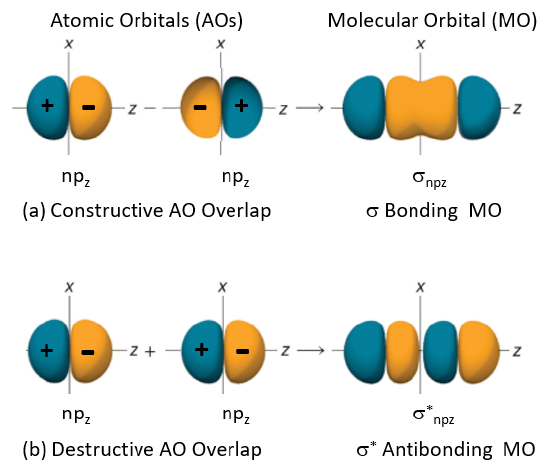
Figure \(\PageIndex{3}\): LCAO-MO approach for combining \(\psi_{p_z}\) along the internuclear axis (z) to form \(\sigma\) and \(\sigma^*\) bonds.
Note, we are NOT saying that the pz of one atom overlaps the pz of another atom along the internuclear axis and this overlap represents the \(\sigma\) bond, that is the valence bond approach. We are saying that there is a MO (molecular orbital) based on nuclear-nuclear, nuclear-electron and electron-electron interactions for the diatomic (two nuclei system), and the MO wavefunction can be described by combining the two AO wavefunctions.
\(\pi\), \(\pi^*\) orbitals
The p orbitals that are orthoganal (perpendicular) to the internuclear axis (z in these drawings) can combine to form both bonding and antibonding orbitals
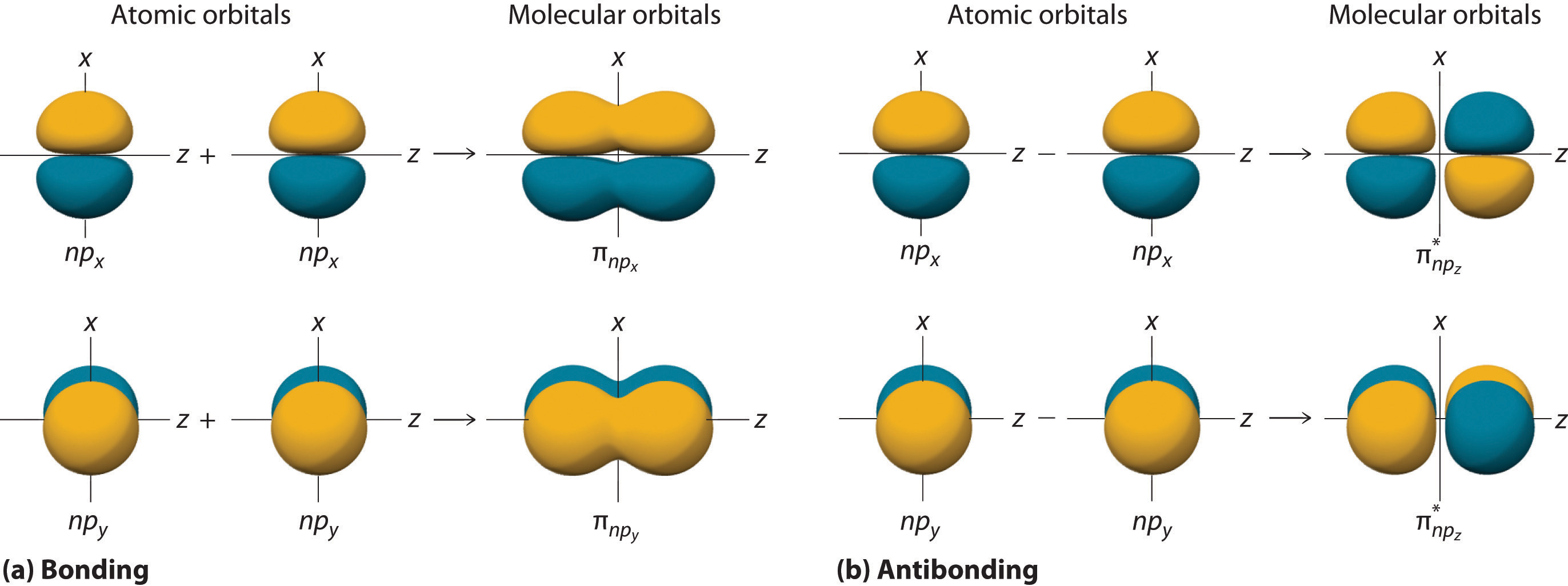
Figure \(\PageIndex{4}\): LCAO-MO approach to combining \(\psi_{p_x}\) or \(\psi_{p_y}\) AO wavefunctions parallel to the internuclear axis (z) to form \(pi\) and \(\pi^*\) bonds. Note the axis is in a nodal plane and there is no electron density along the axis, but the antibonding orbitals have a second nodal plane perpendicular to the axis (xy plane of drawing).
Summary
To distinguish these type of orbitals we need some convention rules:
- \(\sigma\) or (\(\pi\)) refer to bonding orbitals
- \(\sigma^*\) or (\(\pi^*\)) refer to anti-bonding orbitals
An antibonding orbital reduces electron density between the nuclei and causes them to repel each other (it actually creates a node). These are a consequence of the wave-particle duality of the electron.
Note:
In valence bond theory a \(\sigma\) or \(\pi\) bond results from the overlap of two atomic orbital probability density functions of two different bonding atoms \(\psi^2\) and thus there is no concept such as antibonding orbitals. In Molecular orbital theory \(\sigma\) and \(\pi\) bonds are the actual orbital, and one way of identifying MOs is through the LCAO-MO approach, where you combine the actual wavefunctions of the AO (\(\psi\), and thus you can have cancellation of the wavefunction and antibonding orbitals. There are other approaches in quantum mechanics but the LCAO-MO is probably the easiest to visualize.
It should also be noted that the LCAO-MO approach to MO is not the same as hybridization. In hybridization you are combining different \(\psi^2\) of the same atom, in LCAO-MO you are combining \(\psi\) of different atoms. These are completely different approaches.
Bond Order
In section 8.3.3 we introduced the concept of Bond Order and how molecules with resonance structures could have fractional bond orders. MO theory gives an alternative method to approach bond order, which is simply the number of occupied bonding orbitals minus the number of antibonding orbitals. In the next section we will look at MO electron configurations of various diatomic molecules and we can use those to determine the bond order of the bond between the two atoms of the diatomic.
Note, a bond order of zero means there is no bond.
MO Electron Configurations
Calculating the electron configuration of a Molecular Orbital (MO) is similar to the process we used in section 7.2 to calculate the electron configuration of an atomic orbital. Summarizing the rules:
- Count the total number of electrons contributed by each atom
- Aufbau Principle - fill up the lowest energy orbitals first.
- Hund Rule of Maximum Multiplicity (give all electrons in degenerate orbitals the same spin)
- Pauli Exclusion (a MO can only have two electrons, which must be of opposite spin).
The first step is determine the ranking of the orbitals, noting that the number of MOs equals the number of AOs combined to form them, and that the sum of the energies of the bonding and antibonding MOs equals the energy of the AOs that form them. So the the \(\sigma_{1s}\) is lower than the 1s by the same amount of energy that the \(\sigma^*_{1s}\) is higher
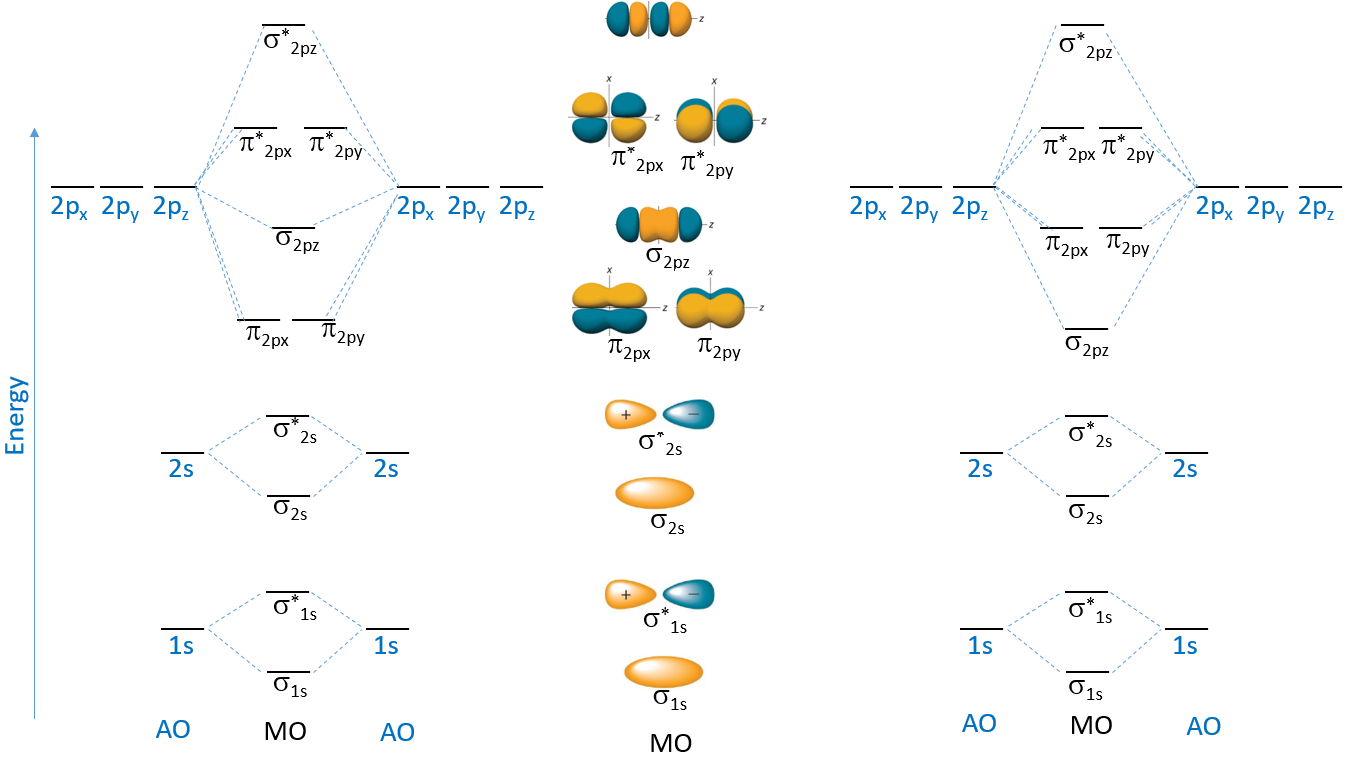
Figure \(\PageIndex{5}\): Relative Energy ranking of different MOs and AOs. On the left and right are the ways the AOs form MOs, and in the middle is a visualization of the MO wavefunctions. Note, there are two different configurations for the MOs formed from the mixing of the 2p AOs.
In calculating the energies of the MOs the electron-electron interactions have an effect. One would expect the \(\sigma_{2p_z}\) to have a greater lowering of energy than the \(\pi_{2p}\), but what you notice in the MO configuration is that there are 2 \(\sigma\) orbitals in the second period, those formed from 2s and 2p interactions along the internuclear axis. Since these are in the same region of space, the filled \(\sigma_{2s}\) orbitals interact with the \(\sigma_{2p}\) more than the \(\pi_{2p}\) and raise its energy, and the left hand ranking of energies is used while filling the bonding orbitals of the second period. Once all the bonding orbitals are filled, there is no lowering of energy, and the right hand part is used. See below.
First Period
The first period only has s orbitals and Figure \(\PageIndex{6}\) shows the electron configuration for diatomic hydrogen and helium.
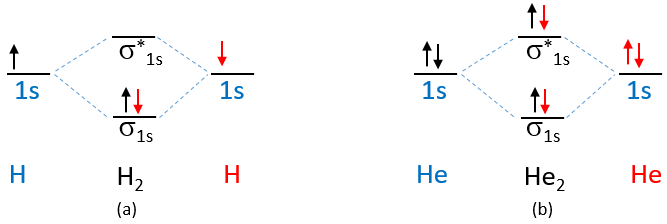
Figure \(\PageIndex{6}\): MO electron configurations of H2 and He2.
The electrons on the AOs of Figure \(\PageIndex{6}\) are color coded to help students keep track of what is going on. In (a) each hydrogen donated one electron, while in (b) each helium donates two electrons.
Exercise \(\PageIndex{7}\)
Based on MO theory, answer the following questions
- What is the bond order of hydrogen?
- What is the bond order of helium?
- Does MO theory predict H2 to be stable, and if so, how?
- Does MO theory predict He2 to be stable, and if so, how?
- Answer a
-
one
- Answer b
-
zero
- Answer c
-
Yes, the bond order is one and there is a lowering of energy by filling the \(\sigma_{1s}\) orbitals of H2 as compared to having one electron is the 1s orbital of each hydrogen.
- Answer d
-
No, the bond order is zero and there is not net stabilization of diatomic helium as compared to monatomic. The stabilization gained by the \(\sigma_{1s}\) bonding orbital is offset by the destabilization of the \(\sigma^*_{1s}\) antibonding orbital
Second Period
Because Helium has a bond order of zero we can ignore the effect of the first period on the electron configuration of the second period. Lithium and beryllium have MO electron configurations analogous to hydrogen and helium except that it is the \(\sigma_{2s}\) and \(\sigma^*_{2s}\) MO that is being filled. In this section we will focus on the filling of the p orbitals. In Figure \(\PageIndex{5}\) we showed two orbital filling diagrams for the p-orbitals, and the general trend for energies is shown in Figure \(\PageIndex{7}\), note diatomics formed from atoms with more than 3 electrons in the p orbital have the \(\sigma_{2p_z}\) lower than the \(\pi_{2p_{xy}}\) (oxygen and fluorine, which are [He]2s22p4 [He]2s22p5 and respectively).
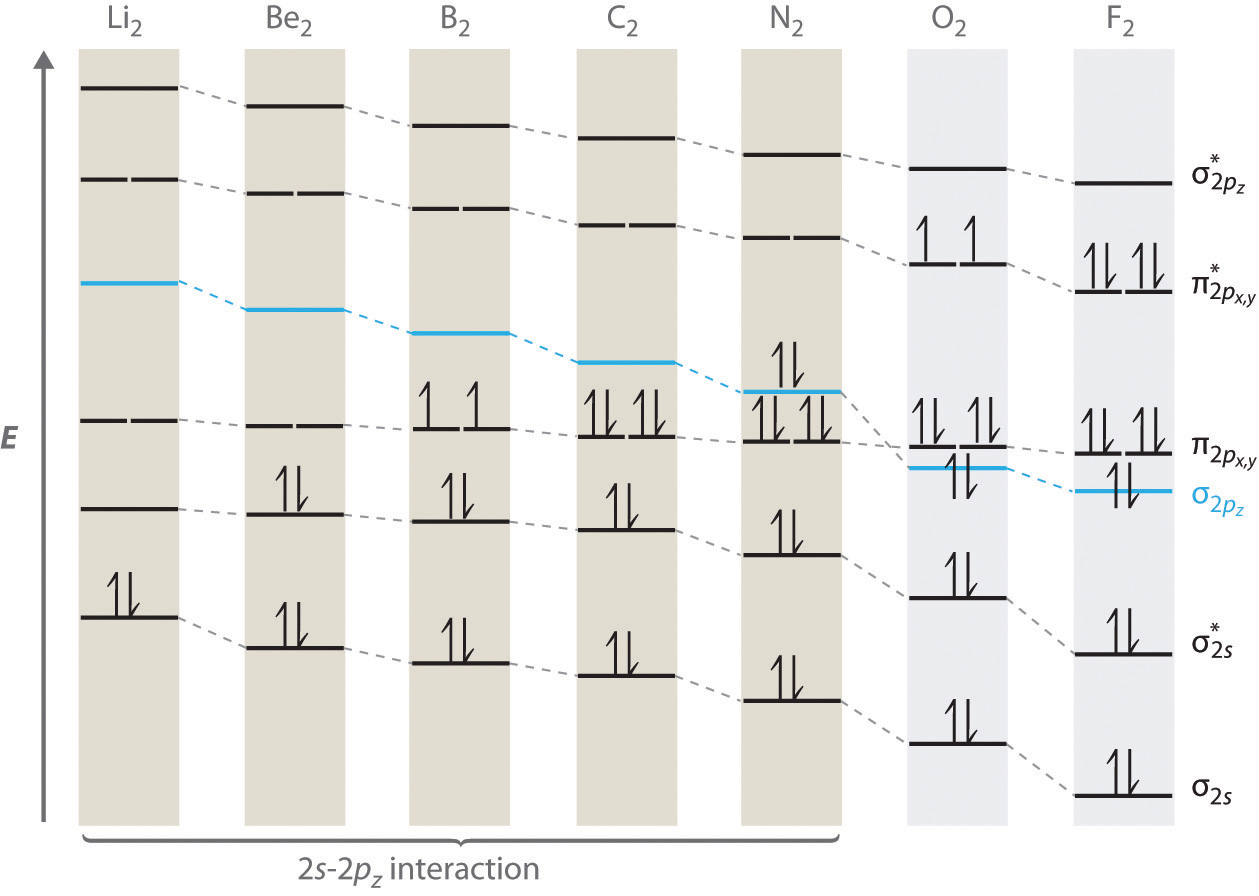
Figure \(\PageIndex{7}\): MO electron configuration of second period homonuclear diatomics.
Note
When we studied the electron configuration of the atoms (section 7.3.1) we noted some interesting behaviors like chromium having an electron configuration of [Ar]:4s13d5 in contrast to the trend of [Ar]:4s23d4, and this was due to the fact that the Coulombic energy of orbitals are influenced by both positive (nuclear) and negative (electron) interactions, and as electrons fill orbitals those interactions can change. The fact that both the \(\sigma_{2s}\) and \(\sigma_{2p}\) have electron density along the internuclear axis means interactions between these orbitals is significant, with the net result that these orbitals "perturb" (mix with) each other in a manner that the \(\sigma_{2p}\) undergoes an increase in energy while the \(\sigma_{2s}\) has a lowering in energy, as shown in Figure \(\PageIndex{8}\). For this mixing to occur the unperturbed orbitals need to be of similar energy. As you go across the periodic table you are increasing the effective nuclear charge and so both the \(\sigma_{2s}\) and \(\sigma_{ps}\) are lowered, but the \(\sigma_{2s}\) has a greater effect (is lowered more) and thus the energy separation between them increases, reducing the ability to mix. This effect becomes negligible after nitrogen, and so for oxygen and fluorine the \(\sigma_{2s}\) is lower in energy thant the \(\pi_{2p}\) the.
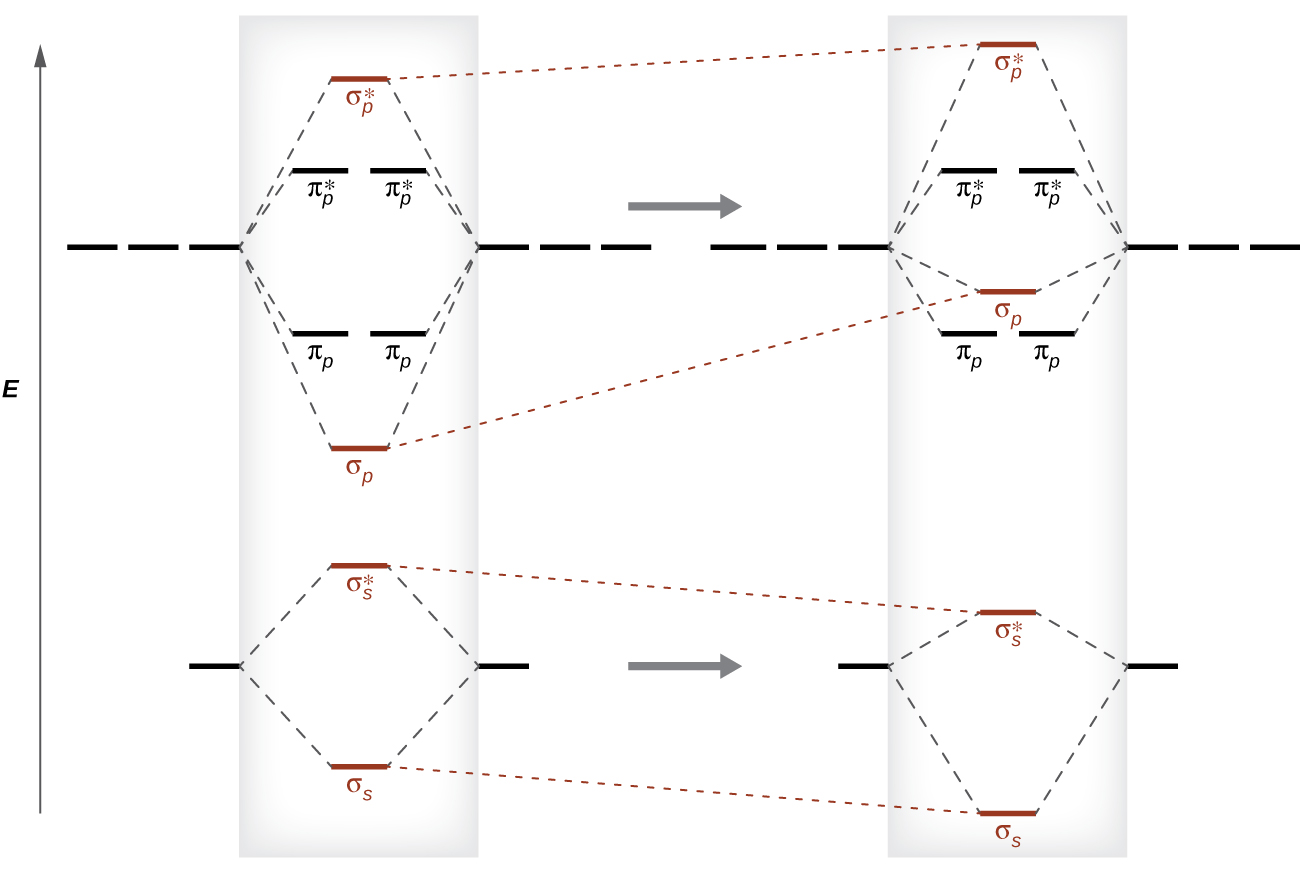
Figure \(\PageIndex{8}\): On the left is the "expected" ordering of energies based on a \(\sigma\) bond having electron density along the internuclear axis and thus resulting in a lower energy than a \(\pi\) bond, which does not have electron density in this region. This trend is only seen in oxygen and fluorine. On the right is the actual ordering of energies until all the bonding orbitals have been filled (Li2-N2). (image credit: OpenStax)
A rigorous discussion of this effect is beyond the scope of this text, but students are required to know that the empty \(\sigma_{2s}\)and \(\sigma_{2p}\) orbitals in a manner that causes the trend in Figures \(\PageIndex{7}\) and \(\PageIndex{8}\).
Writing MO electron configurations.
Atomic electron configurations are written in terms of atomic orbitals and molecular electron configurations are written in terms of molecular orbitals.
| Molecule | Electron Configuration | Bond Order |
|---|---|---|
| Li2 | \((σ_{1s})^2(σ^∗_{1s})^2(σ_{2s})^2\) | 1 |
| Be2 (unstable) | \((σ_{1s})^2(σ^∗_{1s})^2(σ_{2s})^2(σ^∗_{2s})^2\) | 0 |
| B2 | \((σ_{1s})^2(σ^∗_{1s})^2(σ_{2s})^2(σ^∗_{2s})^2(π_{2py},\:π_{2pz})^2\) | 1 |
| C2 | \((σ_{1s})^2(σ^∗_{1s})^2(σ_{2s})^2(σ^∗_{2s})^2(π_{2py},\:π_{2pz})^4\) | 2 |
| N2 | \((σ_{1s})^2(σ^∗_{1s})^2(σ_{2s})^2(σ^∗_{2s})^2(π_{2py},\:π_{2pz})^4(σ_{2px})^2\) | 3 |
| O2 | \((σ_{1s})^2(σ^∗_{1s})^2(σ_{2s})^2(σ^∗_{2s})^2(σ_{2px})^2(π_{2py},\:π_{2pz})^4(π^∗_{2py},π^∗_{2pz})^2\) | 2 |
| F2 | \((σ_{1s})^2(σ^∗_{1s})^2(σ_{2s})^2(σ^∗_{2s})^2(σ_{2px})^2(π_{2py},\:π_{2pz})^4(π^∗_{2py},\:π^∗_{2pz})^4\) | 1 |
| Ne2 (unstable) | \((σ_{1s})^2(σ^∗_{1s})^2(σ_{2s})^2(σ^∗_{2s})^2(σ_{2px})^2(π_{2py},\:π_{2pz})^4(π^∗_{2py},π^∗_{2pz})^4(σ^∗_{2px})^2\) | 0 |
Magnetism
Another success of MO theory is its ability to predict the magnetic properties of diatomics like oxygen, as demonstrated in the following video from BerkeleyChemDemos. Oxygen's MO electron configuration has two unpaired electrons, which makes it a paramagnetic molecule that interact with a magnetic field. On the other hand nitrogen, has no unpaired electrons and is classified as a diamagnetic compound which does not interact with a magnetic field.
- Paramagnetic Substance - molecules that have unpaired electrons with aligned spins that interact with external magnetic fields.
- Diamagnetic Substance - molecule that do not interact with magnetic fields. All the electrons are spin coupled in electron pairs, thus cancelling their net magnetic moment.
- Ferromagnetic Substance - this is the iron based classical magnet and is a result of electron orientations in a metallic bond.
Contributors and Attributions
- Some material modified or adopted through LibreText hyperlibrary from OpenStax, Paul Flowers et. al.,


