8.3: Resonance

Introduction

One of the postulates of the Lewis Dot Structure for representing molecules is that a bond is the result of a pair of electrons being shared between two different nuclei, and as such, can be represented as a line between the two nuclei (the letters that represent the elements involved). But what if the electrons are shared between more than two nuclei? When this happens, there is no one Lewis Dot Structure that accurately describes the molecule. When this happens you need to draw resonance structures, none of which accurately describe the bonds, with the real structure sort of being the average of all the resonance structures. In the next Chapter we will look at the types of bonds in molecules and learn that there are two fundamentally different types of bonds, \(\sigma\) bonds and \(\pi\) bonds. The sigma bonds can be described with Lewis dot structures as they represent bonding electrons shared between two nuclei, but sometimes the \(\pi\) bonds have electrons that are shared over more than two nuclei, in which case no single Lewis dot structure can accurately describe the bond. For example the organic solvent benzene (C₆H₆) has 6 electrons that are shared by all 6 carbons and can form a ring circuit, as depicted in video \(\PageIndex{1}\), and as we shall see, this requires two resonance forms of the Lewis dot structure.

Video \(\PageIndex{1}\): 0'30" YouTube uploaded by S.K. Sinha depicting the delocalized electrons of benzene (C6H6), which prevent one from being able to write one simple Lewis dot structure, and invoking the need for resonance structures. (https://youtu.be/7FyIQ6Sdrpg)

NOTE: Resonance structures represent different ways of placing electrons on the atoms in a molecule's Lewis dot structure. They do not describe different molecules and all resonance structures have the same connectivity. If you change the connectivity, you change the molecule, and that is not a resonance structure. In section 8.5 we will cover drawing Lewis dot structures and you will learn how to recognize if they exist while you are drawing them. But before we draw them, we want to define and describe them. So the following examples should help you identify and describe resonance structures.

Lets start with a look at the Lewis Dot Structure of Ozone

Illustration of Resonance: Ozone

Ozone (O₃) is an allotrope of oxygen, with diatomic oxygen (O₂) being the most common form of oxygen. Ozone is a very reactive form of oxygen that has detrimental health effects (which is why ozone alerts are posted along the highways of cities), but it also reacts with ultraviolet radiation in the upper atmosphere and thus shields the biosphere from the harmful effects of UV radiation. There are two ways of drawing the Lewis dot structure of ozone

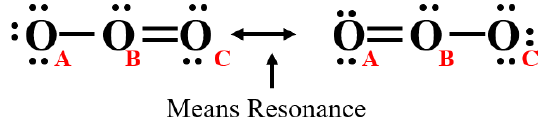
Figure \(\PageIndex{1}\): The two Lewis dot structures of ozone. Note, the two headed arrow means these are not real structures but resonance structures.

That is, from Figure \(\PageIndex{1}\) there is a choice of between which two atoms the double bond goes, oxygen B & C (left) or A & B (right), which is also demonstrated in the video \(\PageIndex{2}\).

Video \(\PageIndex{2}\): 1'15" YouTube uploaded by Selenium demonstrating that there is no single way to draw the Lewis dot structure of Selenium (https://youtu.be/YAyhIo3DnPc)

Figure \(\PageIndex{2}\) shows another way of drawing ozone that indicates the electrons of the second bond in the double bond are actually shared over all three oxygen atoms

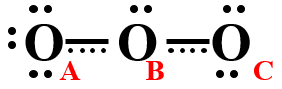
Figure \(\PageIndex{2}\): This image is sort of a mixture of the two resonance structures in Figure \(\PageIndex{1}\), where the electrons of the second bond of the double bond are shared by all three oxygen atoms.

The problem with Figure \(\PageIndex{2}\) is that it does not tell you how many electrons there are (you can't count dots and bars).

Resonance Structures vs. Isomers

It is important to denote the difference between resonance structures and isomers. Resonance structures are not real molecules, but a shortcoming of the postulates that Lewis dot structures are based on, that is, a covalent bond is formed when electrons are shared by two atoms, and thus can be represented by a line between the atoms. In the case of ozone above, the bonding electrons are shared by three atoms, and so no one Lewis dot structure could accurately represent ozone. Isomers are real molecules, Figure \(\PageIndex{3}\) shows two different isomers, hydrogen cyanide (HCN) and hydrogen isocyanide (HNC) and a chemical reaction can occur where these molecules interconvert into each other.

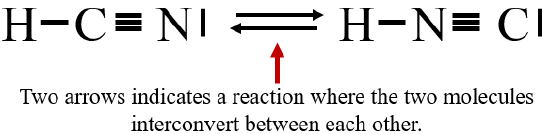
Figure \(\PageIndex{3}\): These are not resonance structures but different molecules, and the two opposing arrows indicates a reaction in both directions occurs.

Note

\(\huge{A\leftrightarrow B}\) - A & B are not two different molecules but different ways of writing the same molecule, they are resonance structures.

\(\huge{A\leftrightarrows B}\) - A & B are two different molecules that can interconvert between each other and form an equilibrium mixture.

Bond Order

Bond order is a way of describing the magnitude of a bond; a single bond has a bond order of 1, double bond 2 and triple bond 3. An individual Lewis dot structure can only have integer bond orders.

Note

For bonds between identical nuclei, the higher the bond order the stronger the bond and the shorter the bond length.

If there are resonance structures, the bond order of the bonds in the resonant structure is the average bond order, which can be determined from any individual resonant structure, and it need not be an integer value.

\[\text{Bond Order}=\frac{\sum\text{bond order of all bonds in a resonance structure} }{\text{number of bonds in resonance structure}}\]

• Bond Order = 1: Single Bond
• Bond Order = 2: Double Bond
• Bond Order = 3: Triple Bond
• Bond Order = 1.5: Combination of Single and Double Bond
• Bond Order = 1.33: Combination of Two Single and one Double Bond

Example \(\PageIndex{1}\)

What is the bond order of the oxygen-oxygen bond in ozone.

Solution

\[\text{Bond Order}=\frac{\text{1 single + 1 double} }{\text{2 bonds}} = \frac{3}{2}=1.5\]

Both bonds in Ozone have a bond order of 1.5 and are the same length, which is longer than a double bond (because the double bond is a stronger bond) and shorter than a single bond (because a single bond is a weaker bond).

Nitrate Ion

The Lewis dot structure of nitrate has three resonance structures. Because it is an ion, it must be in brackets and the charge shown outside the Lewis dot structure.

Figure \(\PageIndex{4}\): Three resonance structures of nitrate ion. Note, for ions, we place the Lewis dot structure in brackets and the charge as a superscript on the outside of the bracket. In section 8.3.5 we will learn how to draw Lewis dot structures, but it needs to be noted that you have extra electrons for anions, and fewer for cations.

If we were to merge the Lewis dot structure into one Figure like we did in fig. 8.3.4 for ozone

Figure \(\PageIndex{5}\) In this Figure we have mixed the three resonance structures in Figure \(\PageIndex{4}\) like was done for ozone in Figure \(\PageIndex{2}\).

Exercise \(\PageIndex{1}\)

What is the bond order for the nitrogen=oxygen bond in nitrate?

Answer

\[\text{Bond Order}=\frac{\text{2 single + 1 double} }{\text{3 bonds}} = \frac{4}{3}=1.33\]

So the bond order of nitrogen is 1.33, that is, it is 2/3 single bond and 1/3 a double bond.

Exercise \(\PageIndex{2}\)

Would you expect the nitrogen-oxygen bond length of nitrate to be closer to the N-O single bond or the N=O double bond?

Answer

It is closer to the single bond in length because a bond order of 1.33 is closer to 1 than it is to 2.

Benzene

Benzene (C₆H₆) is a ring structure that is common in organic compounds known as aromatics and is represented in video \(\PageIndex{1}\) at the beginning of this Chapter. There are two resonance structures for benzene as indicated in Figure \(\PageIndex{5}\).

Figure \(\PageIndex{5}\): Lewis dot structure of benzene explicitly showing the hydrogens

Note, as carbon is in the second period of the periodic table there are no d-orbitals and so carbon can not have an expanded octet, nor is it in group IA, IB or IC, which allow it to have less than an octet. Thus carbon can be considered to follow the octet rule and needs 8 valence electrons in its Lewis dot structure. This allows us to remove the hydrogens from the Lewis dot structure and implicitly infer them. That is, each carbon needs 8 electrons and if the drawing omits 2, we assume there is a hydrogen present.

Figure \(\PageIndex{6}\): Lewis dot structure of benzene with implicit hydrogens

Figures \(\PageIndex{5}\) and \(\PageIndex{6}\) are two ways of drawing benzene and it is important that students become familiar with the convention of Figure \(\PageIndex{6}\). The reason this convention is so common is that the bonds to hydrogen are terminal, in the sense that hydrogen can only have one bond, and this convention of not drawing the hydrogen is common in chemistry, especially organic chemistry.

Figure \(\PageIndex{7}\): Lewis dot structure of benzene showing the delocalization of the electrons across all the carbons.

Exercise \(\PageIndex{3}\)

1. What is the bond order of the carbon-carbon bond in benzene?.
2. Do resonance structures always add up to non-integer bond orders?

Answer a

\[\text{Bond Order}=\frac{\text{3 single + 3 double} }{\text{6 bonds}} = \frac{9}{6}=1.5\]

Answer b

FALSE, look at carbon dioxide, the next example.

Carbon Dioxide

The Lewis dot structure of carbon dioxide is shown in Figure \(\PageIndex{8}\).

Figure \(\PageIndex{8}\): Three resonance structures of carbon dioxide

In the above Figure we see the second and third resonance structures average out to the first, and so the average of all the resonance structures is a double bond. Thus it is common to write carbon dioxide as having two double bonds, and that resonance structure is the correct structure of carbon dioxide.

Exercise \(\PageIndex{4}\)

Calculate the bond order of carbon dioxide from the Lewis dot structures on the left and right of Figure \(\PageIndex{8}\).

Answer

For the structure on the left:

\[\text{Bond Order}=\frac{\text{0 single + 2 double} }{\text{2 bonds}} = \frac{4}{2}=2\]

For the structure on the right:

\[\text{Bond Order}=\frac{\text{1 single + 1 triple} }{\text{2 bonds}} = \frac{4}{2}=2\]

From exercise \(\PageIndex{8}\) it is clear that no matter which resonance structure you use, the bond order is the same. Now even though carbon dioxide has two double bonds, if you are asked to draw it's Lewis dot structure, you should include the two with the single and triple bonds, and this will be covered in section 8.5.

Summary

So what we have seen is that one of the shortcoming of Lewis dot structures comes from the concept that a line represents a bond between two nuclei, but sometimes this is false and the bond is between more than two nuclei. In that case you need to write multiple Lewis dot structures, the resonance structures, and use an arrow with two heads to indicate that each of the individual structures are resonance structure, and the true molecule is a combination of them all. If, as in the case of carbon dioxide, all the resonance structures average out to one of the resonance structures, then it can be treated as the real structure, and you have an integer bond order. If not, the real structure is none of the resonance structures, and the bond order is of non-integer order, often indicated with a dotted line.

It must be emphasized that resonance structures do not show the true bond order and thus do not represent the true structure of the molecule, which results from the combination of all the resonance structures.