8.2: Covalent Bonding and Lewis Structures
- Page ID
- 52843
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Before proceeding do a quick review of "Covalent Bonds and Molecules", (section 2.5.2) of this LibreText. Note in that section we covered the potential well model and provided multiple ways of representing covalently bonded molecules. In this section we are going to develop a type of structural formula called the Lewis Dot Structure. In a Lewis Structure, you draw a molecular structure that accounts for the valence electrons of all the participating atoms, showing the connectivity (bonds) as lines between atoms, and lone electrons as dots. In section 8.6 you will use this lewis dot diagram to predict the three dimensional geometry of a molecule. Be sure to do the attached worksheets that will be at the end of this section
Valence Electrons and Lewis Symbols for atoms
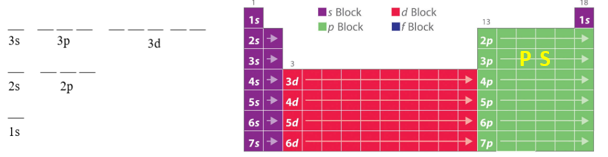
In the last Chapter we recognized that electrons reside in orbitals and that the families of the periodic table had isoelectronic valence shell electron configurations. For the representative elements (s and p blocks) we have the following valence shell electron configurations.
|
|
Note, the s and p-block elements have 4 orbitals (one-s orbital and three p-orbitals), and so the convention is to put one electron in each orbital before pairing them, and to only allow two electrons in an orbital (Pauli Exclusion principle). This means that there are 8 electrons around the central atom if we are filling S & p orbitals, which is the foundation of the octet rule (see below).
Lewis Dot Structure Conventions
There are two types of electrons, lone electrons and bonding electrons. The lone electron is only attracted to one nucleus, the bonding electrons are shared between two nuclei.
- Lone electrons are represented by a dot
- Bonding electrons are represented by a line connecting two nuclei
- Lone Electrons
- Single Electron X\(\large\cdot\) (Single electron in orbit of nuclei X, note; this orbital could accept an additional electron)
- Pair of Electrons X: or X| (spin coupled pair of electrons in an orbital of nuclei X)
- Bonding Electron Pairs
- Single bond X-Y (two electrons shared in a bonding orbital between nuclei X & Y)
- Double bond X=Y (four electrons shared in two bonding orbitals between nuclei X & Y)
- Triple bond X\(\equiv \)Y (6 electrons shared in three bonding orbitals between nuclei X & Y)
Lewis Dot Structures of Diatomics
Hydrogen:
Hydrogen has one electron and one proton. As each orbital would like two electrons, two hydrogens come together and share their electrons, providing the single bonded diatomic hydrogen molecule. Note: Hydrogen only forms one bond in most compounds.

Figure \(\PageIndex{1}\): Diatomic hydrogen
Halogens:
X=F, Cl, Br, or I:
\[\underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{:X}\cdot}} +\underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\cdot\textrm{X:}}} \rightarrow \underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{:X}}} -\underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{X:}}} \]
Oxygen:
\[\underset{\Large{\cdot\cdot\,}}
{\overset{\Large{\cdot}}
{\textrm{:O}\cdot}}+\underset{\Large{\cdot\cdot\,}}
{\overset{\Large{\cdot}}
{\cdot\textrm{O:}}}\rightarrow \underset{\Large{\cdot\cdot\,}}
{
{\textrm{:O}}}=\underset{\Large{\cdot\cdot\,}}
{
{\textrm{O:}}}\]
Nitrogen:
\[\underset{\Large{\cdot\,}}
{\overset{\Large{\cdot}}
{\textrm{:N}\cdot}}+\underset{\Large{\cdot\,}}
{\overset{\Large{\cdot}}
{\cdot\textrm{N:}}}\rightarrow
{
{\textrm{:N}}}\equiv
{
{\textrm{N:}}}\]
Octet Rule
The "octet rule" says that for many molecules the bonds are formed through interaction of the s and p orbitals of the atoms, and so the most stable (correct) electron configuration is when each atom of the molecule has 8 electrons (four filled orbitals) in the valence shell. There are many molecules that do not follow the octet rule, in fact we have already covered one, hydrogen, which can only have one bond (two electrons). There are three types of exception to the octet rule, which are Lewis dot structures with atoms containing:
- less than 8 electrons.
- more than 8 electrons
- an odd number of electrons
Atoms that can have a Reduced Octet
One Electron Pair: Hydrogen always forms one bond and so has a duet (2 electrons). Note, there are cases like diboron (B2H6) that have "bridging hydrogens", which are covalently bonded to two boron. These are very uncommon and in this class, hydrogen always has a duet (two electrons).
Why does hydrogen never follow the octet rule and only has 2 electrons?
The valence orbitals of hydrogen (and helium) have a principle quantum number of 1, and so there is only one orbital available, the 1S. Since each orbital can contain up to two electrons (of opposite spin), hydrogen can have 2 electrons in its Lewis Dot Structure.
Two Electron Pairs: Group IIA atoms like Beryllium often have 4 valence electrons, as in the case of BeH2 and BeF2.

Figure \(\PageIndex{2}\): Lewis dot structure (left) and space filling diagram (right) of BeCl2. Group IIA compounds can have stable structures with two electron pairs (4 electrons) .
Note: The above structure of Beryllium chloride is in the gas phase and the only structure this class is required to understand. In the solid phase Group IIA compounds form ionic not covalent compounds with halogens (and hydrogen). Beryllium, being so small, actually forms a chain like polymer in the solid phase. In this class we only need to be able to draw Lewis dot structures for compounds like the one in Figure Figure \(\PageIndex{2}\).
Three Electron Pairs: Group IIIA atoms like Aluminum can have 6 valence electrons
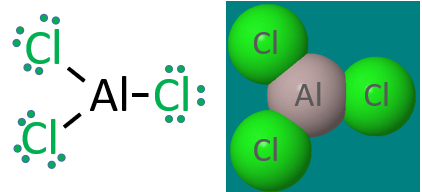
Once again, this Lewis dot structure of covalent aluminum chloride is for the gas phase molecule, and in the solid phase this is an ionic compound and not covalent, in fact it forms a hydrated ionic crystal, aluminum chloride hexahydrate. But if you are asked to draw a Lewis dot structure for a group III halogen (or hydride), the central atom has 3 bonding pairs and not an octet.
Can atoms like Be (Group IIA) and Al (Group IIIA) have an octet?
Yes they can, but they do not need to.
Atoms that can have an Expanded Octet
To have an expanded octet (more than 8 electrons) you need more than 4 orbitals. In the next Chapter we will learn that molecular orbitals are different than atomic orbitals, but one way to describe molecular orbitals is by assuming they are the result of different atomic orbitals mixing with each other, and the number of molecular orbitals must equal the number of atomic orbitals that were mixed to create them. This means that you need to start using d-orbitals, and those are only available for atoms in the third period or above. So atoms in the third period or greater can have expanded octets.
Phosphorous often has 5 orbitals (10 electrons) and sulfur often has 6 orbitals (12 electrons) because they are in the third period (Figure \(\PageIndex{5}\)), but nitrogen and oxygen can never have expanded octets because they are in the second period and there is not such thing as a 2d orbital.
Figure \(\PageIndex{6}\): Lewis dot structures of compounds of phosphorous and sulfur, which being in the third period have available d-orbitals, and so can have more than an octet of electrons.
Exercise \(\PageIndex{1}\)
Why can't elements if the second row have an expanded octet?
- Answer
-
For the second row, the principle quantum number is 2, and so you have s and p orbitals in the valence shell. As there is one type of S, (2s) and three types of P, (px, py & pz), there are only 4 available orbitals, which can take up to 8 electrons (an octet). NOTE: in the next Chapter we will study molecular orbitals, and the orbitals in molecules are not atomic orbitals (s,p,d,f), but are different. That said, the number of molecular orbitals is determined by the number of atomic orbitals in the valence shell, but they are different


