8.4: Formal Charge
- Page ID
- 52857
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
The concept of formal charge is actually very simple. It relates the number of electrons around an atom in a molecule's Lewis dot structure to the number of electrons that atom donated to the Lewis dot structure. In the next section we will cover drawing Lewis dot structures, and the first step is to calculate the number of electrons each atom donates to the molecule, and then to essentially draw a structure based on those electrons, placing them in either bonding or nonbonding orbitals. In formal charge calculations electrons in bonding orbitals are considered to be evenly split between the two bonding atoms, (one is assigned to each atom), while those in lone pair (non bonding orbitals) are assigned to the atom they are placed on.
A negative formal charge means there are more electrons around an atom than it donated, a positive means there are fewer electrons around an atom then it donated, and a neutral formal charge means the number it donated is the same as in the structure.
Some Important Things to Note about Formal Charges
- Formal charges are not real charges, they are a way of looking at electron distributions in a Lewis dot structure. In section 8.7 we will cover electronegativty and molecular polarity, and then we will look at the actual charge distribution in real molecules, which does not always reflect the formal charge distribution.
- The sum of the formal charges of all the atoms in a neutral molecule equals zero
- The sum of the formal charges of all the atoms in an ion equals the charge of the ion.
Uses of Formal Charges
- Formal charges can help identify the more important resonance structures, that is, hitherto we have treated all resonance structures as equal, but this is not always the case.
- The Resonance Structure with the most atoms having Formal charges closest to zero is usually the preferred resonance structure
- Negative formal charges are preferred on more electronegative atoms (see section 8.7: Bond Polarity and Electronegativity)
- Formal charges can help identify the more likely of two isomers, that is, two different structures made from the same set of atoms, like HCN and HNC.
- RULE of THUMB: The best Lewis dot structure has the most atoms with zero formal charge, or the closest to zero.
Calculating Formal Charge:
The following equation determines the formal charge for each atom in a molecule or polyatomic ion. The first part is the number of valence electrons the atom donates to the Lewis dot Structure. From this is subtracted the lone electrons around that atom, and then half the bonding electrons, as they are split between both nuclei of the bond. If this is zero, then the electrons the atom donated to the structure are around the atom. If it is positive, that means the atom contributed more electrons than are around it, and some of "its" electrons are around other atoms. If it is negative, that means there are more electrons around it than it contributed to the Lewis dot structure.
\[\text{Atoms Formal Charge = [valence electrons] - [lone pair electrons]}-\frac{\text {bonding electrons}}{2}\]
Example \(\PageIndex{1}\)
Calculate the formal charge of all atoms in H-C\(\equiv \)N: and H-N\(\equiv \)C:
Solution
For hydrocyanic acid(H-C\(\equiv \)N:) we get the formal charges of:
H=1-0-1/2(2)=0
C=4-0-1/2(8)=0
N=5-2-1/2(6)=0
For hydrogen isocyanide (H-N\(\equiv \)C:), we get the formal charges of
H=1-0-1/2(2)=0
N=5-0-1/2(8)=+1
C=4-2-1/2(6)=-1
So from the above example, HCN is the preferred structure (isomer) to HNC.
Intuitive Visualization:
Let's use different symbols to represent the electrons and show the bonds as electron pairs (next to each other) instead of lines. In Figure 8.4.1 we see that hydrogen donates one electron (the star), diamond donates 4 (the diamonds) and nitrogen donates 5 (the circles)
Figure \(\PageIndex{1}\): Using stars (hydrogen), diamonds (carbon) and circles (nitrogen) to represent the electrons each atom donates.
From Figure \(\PageIndex{1}\) it is clear the there are 10 valence electrons in a compound made from H,C and N, with hydrogen donating 1, carbon 4 and nitrogen 5. Since hydrogen must be terminal (it can't have two bonds and connect two other atoms), there are only two possible isomers, HCN and HNC. Figure \(\PageIndex{2}\) shows the ways these electrons can combine to form the bonds and lone pairs.
Using the above symbols we get the following Lewis dot structures.
Figure \(\PageIndex{2}\): Lewis dot structures using stars, diamonds and circles to represent the electrons donated from Hydrogen (1 star), Carbon (4 diamonds) and Nitrogen (5 circles) respectively.
Example \(\PageIndex{1}\) showed that all atoms of the left structure of Figure \(\PageIndex{2}\) (hydrogen cyanide) had zero formal charge, while for the right structure (hydrogen isocyanide) the nitrogen had a +1 and the carbon a -1. This is clear to see in Figure \(\PageIndex{2}\), where one of the dots on the right side is near a carbon, meaning one of the electrons nitrogen donated is near the carbon.
Exercise \(\PageIndex{1}\)
Which would be predicted to be more stable, hydrogen cyanide or hydrogen isocyanide
- Answer
-
Hydrogen cyanide because all the atoms have zero formal charges.
It must be emphasized that there are limitations to applying formal charges in determining the stabilty of a compound. It is logical that Lewis dot structures that place electrons near the atom that donates are more likely than structures that place them far away on other atoms.
Exercise \(\PageIndex{2}\)
Consider the two possible structures of acetic acid, CH3COOH
a. 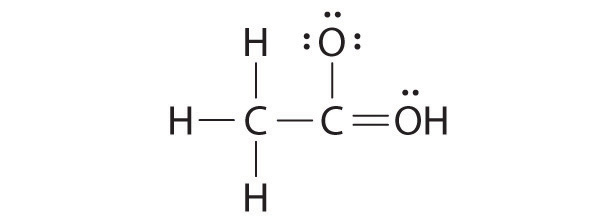 |
b. 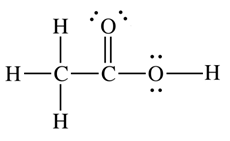 |
- For structure (a), what is the formal charge on the oxygen with three lone pairs?
- For structure (a), what is the formal charge on the oxygen with the hydrogen atom?
- For structure (b), what is the formal charge on the oxygen with no hydrogen?
- For structure (b), what is the formal charge on the oxygen with the hydrogen atom?
- Which is the better Lewis dot structure for acetic acid?
- Answer a
-
-1
- Answer b
-
+1
- Answer c
-
0
- Answer d
-
0
- Answer e
-
Structure (b) because all the formal charges are zero
Formal Charge and Free Radicals
A free radical is a molecule that has one electron. Free radicals are very reactive and there are very few stable free radicals. For example, atomic chlorine is a free radical, \(\underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{:Cl}\cdot}}\) , and two of them will combine to form a bond, which is why chlorine is a diatomic
\( \underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{:Cl}\cdot}} +\underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\cdot\textrm{Cl:}}}\) \( \rightarrow\) \(\underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{:Cl}}} -\underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{Cl:}}}\)
Lets look at two resonance structures of NO2.
\(\underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{O}}}={\overset{\Large{\cdot\cdot}}
{\textrm{N}}}- \underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{O}\cdot}}\) \(\longleftrightarrow\)\(\underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{O}}}={\overset{\Large{\cdot}}
{\textrm{N}}}- \underset{\Large{\cdot\cdot}}
{\overset{\Large{\cdot\cdot}}
{\textrm{O:}}}\)
In the left resonance structure, all the atoms have zero formal charge, while on the right structure, the nitrogen has a +1 formal charge, and the oxygen with the single bond has a -1 formal charge.
Can you draw two additional resonance structures for the above molecules?
Yes, just switch the single and double bonds for the above two structures (with the oxygens and their lone electrons).


