8.9: Covalent Bond Properties: Order, Length, and Energy

Introduction

The covalent bond involves the electrostatic interactions of valence electrons and multiple nuclei of the atoms that form the bond. There are both attractive forces between opposite charges, and repulsive forces between like charges, and these can be described by Coulomb's law:

\[ E= k\dfrac{q_1q_2}{(4\pi\epsilon_0) r} \; \; \; \; \; \; \; \; F=k \dfrac{q_1q_2}{(4\pi\epsilon_0) r^2}\]

• E is the bond energy
• F is the force
• r is the distance of separation between charged particles (note that the potential goes to zero when they are separated by infinity)
• q₁, q₂ are the charges of the respective species interacting

The potential well diagram of a homonuclear diatomic is a good way to understand a covalent bond as illustrated for hydrogen in Figure 8.9.1. It needs to be understood that a bond is dynamic, with the atoms oscillating around an equilibrium distance, which we call the bond length. This oscillation can be understood by looking at Figure \(\PageIndex{1}\). Region (1) shows the atoms completely separated. As they come closer together the electrons of each atom start being attracted to the nuclei of the other atom as in region (2), which lowers the energy and causes a bond. As the atoms keep moving closer the nuculear-nuclear repulsion start to become significant, and in region (4) the energy increases and the atoms move apart. Region (3) is the equilibrium bond length which represents the bottom of the potential well and is the length at which the molecules oscillate back and forth around.

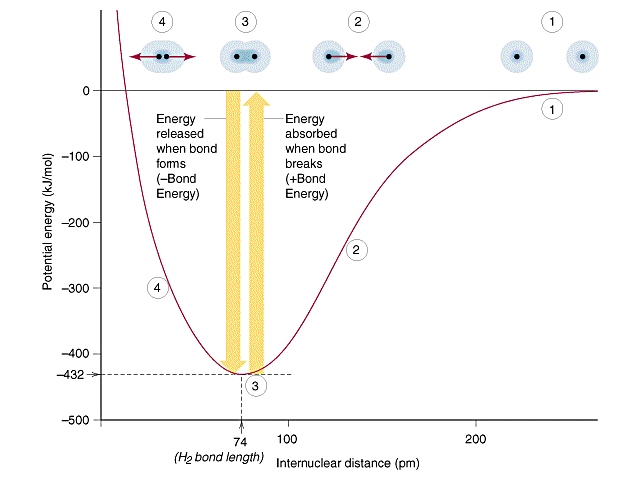Figure \(\PageIndex{1}\): Potential Well Diagram for H₂, where the energy of the H-H bond is plotted as a function of the internuclear distance (radius)

From eq. 8.9.1 we note that when the atoms are separated by infinity (r=infinity) the energy is being divided by infinity, which means it is infinitesimally small and thus equals zero. This means the bond itself has a negative energy and the bond dissociation energy is the endothermic energy you must add to break a bond. Note, this also indicates why opposite charges attract, as that lowers the energy of the bonded particles when compared to the separated particles. It is important that you remember that any bond can be written as a "formation" (exothermic) or dissociation (endothermic) process.

Generic Bond Dissociation

If we look at a generic covalent bond as two electrons being represented as two shared electrons, we see there are two basic ways to break the bond, homolytically and heterolytically. In the former case, each of the separated species has one electron, making them free radicals (species with a lone electron), while the second forms ions, with one species having both electrons and the other having none.

Homolytic bond cleavage
\[A-B \rightarrow A\cdot + B\cdot \]

Heterolytic bond cleavage
\[A-B \rightarrow A^+ + B:^- \\ or \\ A-B \rightarrow A:^- + B^+ ​\]

The potential well diagram in Figure 8.9.1 represents homolytic bond cleavage, which is the type we will discuss in this section. Remember, bond formation is the opposite of dissociation, and so can be visualized as the overlap of two orbitals on two different atoms that contribute one electron each (as indicated in fig. 8.9.1). There is another type of bond called the dative coordinate covalent bond, where one atom provides both electrons that are shared through the overlap with a vacant orbital on another atom.

Bond Order

The bond order is the number of covalent bonds in a chemical bond and the concept was introduced when we covered resonance structures.

Table 4.6.1 Bond Lengths and Bond Dissociation Energies for Bonds with Different Bond Orders in Selected Gas-Phase Molecules at 298 K

Compound	Bond Order	Bond Length (pm)	Bond Dissociation Energy (kJ/mol)	Compound	Bond Order	Bond Length (pm)	Bond Dissociation Energy (kJ/mol)
H3C–CH3	1	153.5	376	H3C–NH2	1	147.1	331
H2C=CH2	2	133.9	728	H2C=NH	2	127.3	644
HC≡CH	3	120.3	965	HC≡N	3	115.3	937
H2N–NH2	1	144.9	275.3	H3C–OH	1	142.5	377
HN=NH	2	125.2	456	H2C=O	2	120.8	732
N≡N	3	109.8	945.3	O=C=O	2	116.0	799
HO–OH	1	147.5	213	C≡O	3	112.8	1076.5
O=O	2	120.7	498.4

Table 8.9.1: Sources: Data from CRC Handbook of Chemistry and Physics (2004); Lange’s Handbook of Chemistry (2005); http://cccbdb.nist.gov.

Fractional Bond Orders and Resonance Structures: Lewis dot structures represent a bond as a line between two atoms and sometimes \(Pi\) electrons are shared between more than two atoms and you need to draw multiple resonance strcutures to accurately describe the molecule. In these cases you can have fractional bond orders.

Figure \(\PageIndex{2}\): Lewis dot structure of nitrate, where the actual bond order is 1.33

In the case of nitrate (Figure 8.9.2) we see there are three resonance structures with each representing 2 single and one double bond, and if we look at each NO bond, two of the structures are single and one is double, for a total bond order of 4 across 3 structures, and so the bond order is 4/3 or 1.33. That is, the real molecule does not have two single and one double bond, but has three identical bonds of order 1.33.

What is the bond order of the CO bond in carbon dioxide?

Figure \(\PageIndex{3}\): Resonance structures for carbon dioxide.

The CO bond order is two, as across the three resonance structures each bond is either 2, 3 or 1, for a total of 6. As there are 3 structures, the bond order of 6/3 or 2.

Bond Length

A bond is not static but dynamic with the atoms undergoing the attractive and repulsive forces as described in the potential well (fig. 8.9.1), where the bottom of the well represents the equilibrium position of the oscillating atoms, which we call the bond length. Table 8.9.1 shows bond lengths for a variety of bonds. Please note that this particular table is in picometers (10^-12), and that a common unit for bond length is the Angstrom Å (10^-10), so for example, the O=O bond is 1.207 Å.

Coulomb's law states that the bond energy is inversely related to the bond length (r), and so factors which influence a bond's strength influence its length. This can allow us to determine some trends in bond lengths.

Some trends in bond lengths for homologous series (where one atom is constant and another is changed)

• Bond length increases going down the periodic table. (smaller atoms make smaller bonds)
  H-F < H-Cl < H-Br < H-I
• Bond length decreases going across the periodic table. (smaller atoms make smaller bonds)
  C-C > C-N > C-O
• For bonds between equivalent atoms, the greater bond order the shorter the bond length
  C\(\equiv \)C > C=C < C-C
  Thus the NO bond of Nitrate, (fig. 8.9.2) is greater than N-O and less than N=O

Bond Dissociation Enthalpy

The IUPAC definition for bond dissociation energy, D, is "the enthalpy (per mole) required to break a given bond of some specific molecular entity by homolysis, e.g. for \(CH_{4}\rightarrow \cdot CH_{3)} + H\cdot\), (IUPAC Gold Book) and the "mean bond energy" is "the average value of the gas phase bond dissociation energies (usually at a temperature of 298K) for all bonds of the same type within the same chemical species.

Table \(\PageIndex{2}\) Energies for the successive breakup of C-H bonds in methane Source: Data from CRC Handbook of Chemstry and Physics (2004)K.

Reaction	D (kJ/mol)
CH4(g) → CH3(g) + H(g)	439
CH3(g) → CH2(g) + H(g)	462
CH2(g) → CH(g) + H(g)	424
CH(g) → C(g) + H(g)	338

Average bond energies can be tabulated as in table \(\PageIndex{3}\) and it needs to be emphasized that these values are average energies. One uese of these tables is that you can determine the enthalpy of reaction if you know the structure of all species in a balanced chemical equation.

\[ ΔH_{rxn} \approx \sum{\text{(bond energies of bonds broken)}}−\sum{\text{(bond energies of bonds formed)}}\]

Single Bonds										Multiple Bonds
H–H	432	C–C	346	N–N	≈167	O–O	≈142	F–F	155	C=C	602
H–C	411	C–Si	318	N–O	201	O–F	190	F–Cl	249	C≡C	835
H–Si	318	C–N	305	N–F	283	O–Cl	218	F–Br	249	C=N	615
H–N	386	C–O	358	N–Cl	313	O–Br	201	F–I	278	C≡N	887
H–P	≈322	C–S	272	N–Br	243	O–I	201	Cl–Cl	240	C=O	749
H–O	459	C–F	485	P–P	201	S–S	226	Cl–Br	216	C≡O	1072
H–S	363	C–Cl	327	S–F	284	Cl–I	208	N=N	418
H–F	565	C–Br	285	S–Cl	255	Br–Br	190	N≡N	942
H–Cl	428	C–I	213	S–Br	218	Br–I	175	N=O	607
H–Br	362	Si–Si	222	I–I	149	O=O	494
H–I	295	Si–O	452	S=O	532
Table \(\PageIndex{3}\): Average Bond Energies (kJ/mol) for Commonly Encountered Bonds at 273 K. Source: Data from J. E. Huheey, E. A. Keiter, and R. L. Keiter, Inorganic Chemistry, 4th ed. (1993).

Trends in Bond Dissociation Energy

There are 3 trends we can observe with bond energies. You should be able to relate these trends to the bond length trends (above).

1. Bonds with hydrogen (H-X) decrease in strength as we go down a column of the periodic table.

H-F > H-Cl > H-Br > H-I

2. Bonds between like atoms generally become weaker going down a column of the periodic table

Cl-Cl > Br-Br > F-F > I-I

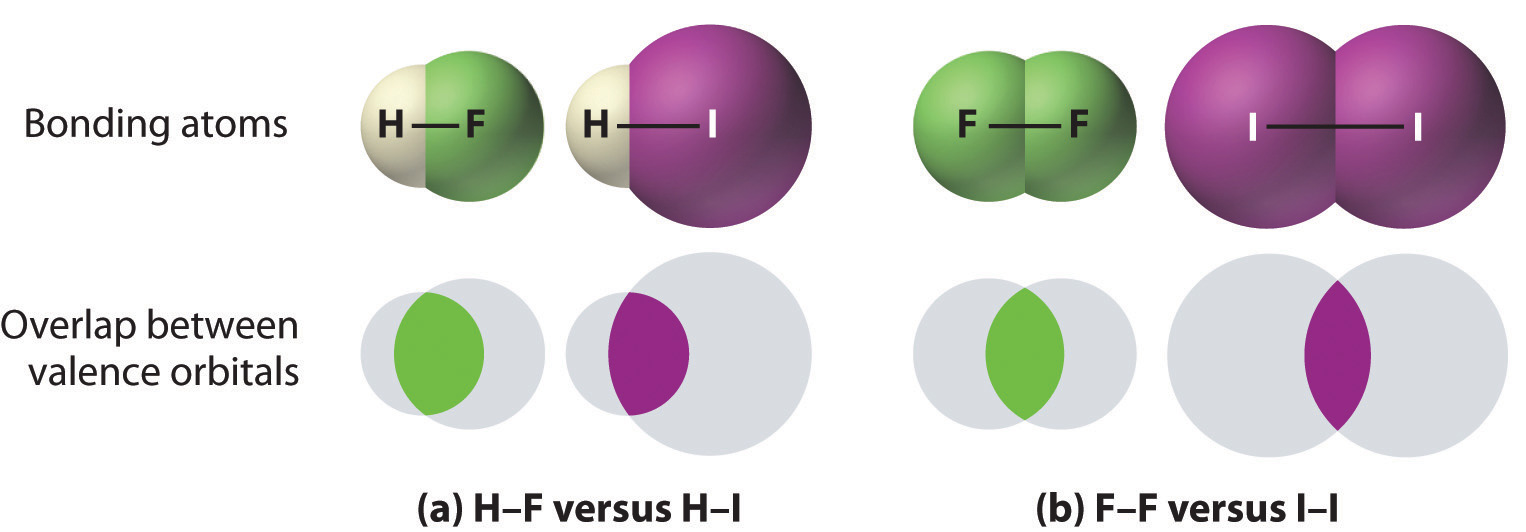
Figure \(\PageIndex{1}\) shows trends (1) & (2) as being results of the trends in atomic radii (as you move down a period atoms take up more volume), and since the bond energy from Coulomb's law is inversely proportional to the distance (1/r) between the atoms, the smaller atoms form stronger bonds. By being closer, a greater percent of the orbitals overlap and this results in stronger bonding interactions.

3. Bond Strength increases as Bond Order Increases

C≡C < C=C < C-C

Enthalpies of Reaction from Bond Dissociation Energies

Since enthalpy is a state function (path independent), we can choose a reaction path where we break all the bonds of the reactants and then form the reactants by creating new bonds. The first step is the summation of their Bond Dissociation Energies (D) for the reactants. The second step is the formation of the products, which is the opposite of their dissociation, so we subtract the sum of their dissociation records.

\( ΔH_{rxn} \approx \sum{\text{(bond energies of bonds broken)}}−\sum{\text{(bond energies of bonds formed)}}\)

Why is subtracting the bond dissociation energies the same as their formation energies?

First Law of Thermodynamics states energy of the universe is conserved, and so if a process is endothermic in one direction (bond dissociation), it must be exothermic by the same quantity in the opposite direction (bond formation).

There is sort of a three step process, and you must draw Lewis dot structures in order to identify the bonds.

1. Balance equation
2. write Lewis dot structures of all species so you can identify bonds
3. Apply the equation:
   \( ΔH_{rxn} \approx \sum{\text{(bond energies of bonds broken)}}−\sum{\text{(bond energies of bonds formed)}}\)

Bond Dissociation Problem:

Using bond dissociation energies calculate the molar enthalpy of combustion for acetic acid.

Video \(\PageIndex{1}\): 7'49" YouTube going over bond dissociation energies

Contributors and Attributions

Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, [e-mail]. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to: