9.1: Orbitals and Theories of Chemical Bonding
- Page ID
- 52897
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
In Chapter 7 we described atomic orbitals for the hydrogen-like atom, based on the wavefunction of an electron in a spherical harmonic orbital around a positive nuclei and then we extended it to the multi-electron atom. In each of these cases we were describing an isolated atom. In a molecule there is more than one nucleus, and so the wavefunction will be different. There are two basic approaches we will take to describing molecular orbitals, the valence bond approach and the molecular orbital approach. We will also identify two different types of molecular orbitals, \(\sigma\) and \(\pi\).
\(\sigma\) orbitals: These are orbitals that have electron density along the internuclear axis, and the sigma bonding orbitals from valence bond theory account for the VSEPR orientations.
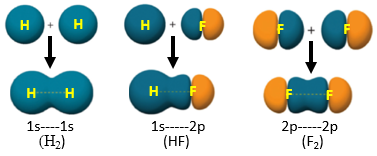
Figure \(\PageIndex{1}\): Sigma bonds have overlap along the internuclear axis. Here we see the sigma bonds formed from the overlap of two s orbitals (H2), an s and a p orbital (HF) and two p orbitals (F2).
\(\pi\) orbitals: These orbitals result from the overlap of p orbitals and have a node along the internuclear axis. They are involved in multiple bonds. So a double bond is 1 \(\sigma\) and 1 \(\pi\), while a triple bond is a \(\sigma\) and 2 \(\pi\)s.
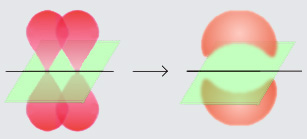
Figure \(\PageIndex{2}\): \(\pi\) bonds result from the overlap of p orbitals that are not oriented along the internuclear axis. If the green plane is the xy plane, then the red p orbitals could be the pz orbital and they could form a \(\pi\) bond with electron density above and below the axis. (image credit JoJan, commons.wikimedia.org/wiki/File:Pi-bond.jpg)
The above two images show the types of overlap involving atomic s and p orbitals. But in molecular systems these are often not appropriate to describe molecular orbitals, and so we are going to look at two different approaches to molecular orbitals, Valence Bond Theory and Molecular Orbital Theory
Valence Bond Theory
Valence Bond (VB) Theory: In section 9.2 we cover Valence bond theory, where we treat the molecular orbitals that result in the VSEPR orientations as being the result of the hybridization of atomic orbitals (s,p,d,...), that is, atomic orbitals mix to form molecular orbitals. There are several things to recognize for two orbitals to "mix". First, the number of molecular orbitals produced equals the number of atomic orbitals mixed. Second, the atomic orbitals being mixed need to be of similar energy. Third, the resulting molecular orbitals acquire the geometry, nodal features and orientation of the orbitals that are mixed. So if you mix an s orbital with a p, it will have a shape that is half S and half P in characteristics. Valence Bond Theory can account for VSEPR geometries, but fails on some more advanced topics like some magnetic properties, or the concept of antibonding orbitals. To understand these we need to take a more complicated approach, molecular orbital theory. But there is a lot of value to valence bond theory and chemists use it all the time.
Molecular Orbital Theory
Molecular Orbital (MO) Theory: Molecular orbital theory is the direct quantum mechanical solution to the multi-nuclei wave function. These result in two types of wave functions, bonding and antibonding orbitals. In section 9.3 we will look at this for the simplest case, the homonuclear and heteronuclear diatomic. We will also look at magnetic properties like paramagnetism and show how MO theory can account for these types of properties in molecules like diatomic oxygen, when valence theory does not.


