5.7: Enthalpy Calculations
- Page ID
- 52112
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Define Hess's Law and relate it to the first law of thermodynamics and state functions
- Calculate the unknown enthalpy of a reaction from a set of known enthalpies of combustion using Hess's Law
- Define molar enthalpy of formation of compounds
- Calculate the molar enthalpy of formation from combustion data using Hess's Law
- Using the enthalpy of formation, calculate the unknown enthalpy of the overall reaction
- Calculate the heat evolved/absorbed given the masses (or volumes) of reactants.
Hess's Law
Hess's Law states that if you can add two chemical equations and come up with a third equation, the enthalpy of reaction for the third equation is the sum of the first two. This is a consequence of the First Law of Thermodynamics, the fact that enthalpy is a state function, and brings for the concept of coupled equations.
Coupled Equations: A balanced chemical equation usually does not describe how a reaction occurs, that is, its mechanism, but simply the number of reactants in products that are required for mass to be conserved. In reality, a chemical equation can occur in many steps with the products of an earlier step being consumed in a later step. For example, consider the following reaction phosphorous reacts with oxygen to from diphosphorous pentoxide (2P2O5)
\[P_4+5O_2 \rightarrow 2P_2O_5\]
and then the product of that reaction in turn reacts with water to form phosphorus acid
\[2P_2O_5 +6H_2O \rightarrow 4H_3PO_4\]
In the above equation the P2O5 is an intermediate, and if we add the two equations the intermediate can cancel out. Hess's law states that if two reactions can be added into a third, the energy of the third is the sum of the energy of the reactions that were combined to create the third.
\[\begin{align} \text{equation 1: } \; \; \; \; & P_4+5O_2 \rightarrow \textcolor{red}{2P_2O_5} \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;\; \; \; \;\Delta H_1 \nonumber \\ \text{equation 2: } \; \; \; \; & \textcolor{red}{2P_2O_5} +6H_2O \rightarrow 4H_3PO_4 \; \; \; \; \; \; \; \; \Delta H_2 \nonumber\\ \nonumber \\ \text{equation 3: } \; \; \; \; & P_4 +5O_2 + 6H_2O \rightarrow 3H_3PO_4 \; \; \; \; \Delta H_3 \end{align}\]
Enthalpy is a state function which means the energy change between two states is independent of the path. Since equation 1 and 2 add to become equation 3, we can say:
\[\Delta H_3=\Delta H_1+ \Delta H_2\]
Hess's Law says that if equations can be combined to form another equation, the enthalpy of reaction of the resulting equation is the sum of the enthalpies of all the equations that combined to produce it.
tepwise Calculation of \(ΔH^\circ_\ce{f}\)
Using Hess’s Law Determine the enthalpy of formation, \(ΔH^\circ_\ce{f}\), of FeCl3(s) from the enthalpy changes of the following two-step process that occurs under standard state conditions:
\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{20px}ΔH°=\mathrm{−341.8\:kJ} \nonumber\]
\[\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm \nonumber{−57.7\:kJ} \]
Solution
We are trying to find the standard enthalpy of formation of FeCl3(s), which is equal to ΔH° for the reaction:
\[\ce{Fe}(s)+\frac{3}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH^\circ_\ce{f}=\:? \nonumber\]
Looking at the reactions, we see that the reaction for which we want to find ΔH° is the sum of the two reactions with known ΔH values, so we must sum their ΔHs:
\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{59px}ΔH°=\mathrm{−341.8\:kJ}\\ \underline{\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm{−57.7\:kJ}}\\ \ce{Fe}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{43px}ΔH°=\mathrm{−399.5\:kJ} \nonumber\]
The enthalpy of formation, \(ΔH^\circ_\ce{f}\), of FeCl3(s) is −399.5 kJ/mol.
Exercise \(\PageIndex{1}\)
Calculate ΔH for the process:
\[\ce{N2}(g)+\ce{2O2}(g)⟶\ce{2NO2}(g) \nonumber\]
from the following information:
\[\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g)\hspace{20px}ΔH=\mathrm{180.5\:kJ} \nonumber\]
\[\ce{NO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH=\mathrm{−57.06\:kJ} \nonumber\]
- Answer
-
66.4 kJ
Here is a less straightforward example that illustrates the thought process involved in solving many Hess’s law problems. It shows how we can find many standard enthalpies of formation (and other values of ΔH) if they are difficult to determine experimentally.
A More Challenging Problem
Using Hess’s Law Chlorine monofluoride can react with fluorine to form chlorine trifluoride:
(i) \(\ce{ClF}(g)+\ce{F2}(g)⟶\ce{ClF3}(g)\hspace{20px}ΔH°=\:?\)
Use the reactions here to determine the ΔH° for reaction (i):
(ii) \(\ce{2OF2}(g)⟶\ce{O2}(g)+\ce{2F2}(g)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−49.4\:kJ}\)
(iii) \(\ce{2ClF}(g)+\ce{O2}(g)⟶\ce{Cl2O}(g)+\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{+205.6\: kJ}\)
(iv) \(\ce{ClF3}(g)+\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+266.7\: kJ}\)
Solution
Our goal is to manipulate and combine reactions (ii), (iii), and (iv) such that they add up to reaction (i). Going from left to right in (i), we first see that \(\ce{ClF}_{(g)}\) is needed as a reactant. This can be obtained by multiplying reaction (iii) by \(\frac{1}{2}\), which means that the ΔH° change is also multiplied by \(\frac{1}{2}\):
\[\ce{ClF}(g)+\frac{1}{2}\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\frac{1}{2}\ce{OF2}(g)\hspace{20px} ΔH°=\frac{1}{2}(205.6)=+102.8\: \ce{kJ} \nonumber\]
Next, we see that \(\ce{F_2}\) is also needed as a reactant. To get this, reverse and halve reaction (ii), which means that the ΔH° changes sign and is halved:
\[\frac{1}{2}\ce{O2}(g)+\ce{F2}(g)⟶\ce{OF2}(g)\hspace{20px}ΔH°=+24.7\: \ce{kJ} \nonumber\]
To get ClF3 as a product, reverse (iv), changing the sign of ΔH°:
Now check to make sure that these reactions add up to the reaction we want:
\[\begin {align*}
&\ce{ClF}(g)+\frac{1}{2}\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\frac{1}{2}\ce{OF2}(g)&&ΔH°=\mathrm{+102.8\: kJ}\\
&\frac{1}{2}\ce{O2}(g)+\ce{F2}(g)⟶\ce{OF2}(g)&&ΔH°=\mathrm{+24.7\: kJ}\\
&\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)⟶\ce{ClF3}(g)+\ce{O2}(g)&&ΔH°=\mathrm{−266.7\:kJ}\\
&\overline{\ce{ClF}(g)+\ce{F2}⟶\ce{ClF3}(g)\hspace{130px}}&&\overline{ΔH°=\mathrm{−139.2\:kJ}}
\end {align*}\]
Reactants \(\frac{1}{2}\ce{O2}\) and \(\frac{1}{2}\ce{O2}\) cancel out product O2; product \(\frac{1}{2}\ce{Cl2O}\) cancels reactant \(\frac{1}{2}\ce{Cl2O}\); and reactant \(\dfrac{3}{2}\ce{OF2}\) is cancelled by products \(\frac{1}{2}\ce{OF2}\) and OF2. This leaves only reactants ClF(g) and F2(g) and product ClF3(g), which are what we want. Since summing these three modified reactions yields the reaction of interest, summing the three modified ΔH° values will give the desired ΔH°:
Exercise \(\PageIndex{2}\)
Aluminum chloride can be formed from its elements:
(i) \(\ce{2Al}(s)+\ce{3Cl2}(g)⟶\ce{2AlCl3}(s)\hspace{20px}ΔH°=\:?\)
Use the reactions here to determine the ΔH° for reaction (i):
(ii) \(\ce{HCl}(g)⟶\ce{HCl}(aq)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−74.8\:kJ}\)
(iii) \(\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{−185\:kJ}\)
(iv) \(\ce{AlCl3}(aq)⟶\ce{AlCl3}(s)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+323\:kJ/mol}\)
(v) \(\ce{2Al}(s)+\ce{6HCl}(aq)⟶\ce{2AlCl3}(aq)+\ce{3H2}(g)\hspace{20px}ΔH^\circ_{(v)}=\mathrm{−1049\:kJ}\)
- Answer
-
−1407 kJ
We also can use Hess’s law to determine the enthalpy change of any reaction if the corresponding enthalpies of formation of the reactants and products are available.
Calculating Enthalpy of Reaction from Combustion Data
In section 5.6.3 we learned about bomb calorimetry and enthalpies of combustion, and table \(\PageIndex{1}\) contains some molar enthalpy of combustion data. In this section we will use Hess's law to use combustion data to calculate the enthalpy of reaction for a reaction we never measured. In fact, it is not even a combustion reaction.
Table \(\PageIndex{1}\) Heats of combustion for some common substances. Note, these are negative because combustion is an exothermic reaction. They are often tabulated as positive, and it is assumed you know they are exothermic. Also, these are not reaction enthalpies in the context of a chemical equation (section 5.5.2), but the energy per mol of substance combusted.
Note: tips for hess's law calculations
The following tips should make these calculations easier to perform
- Write the equation you want on the top of your paper, and draw a line under it.
- From data tables find equations that have all the reactants and products in them for which you have enthalpies.
- If an equation has a chemical on the opposite side, write it backwards and change the sign of the reaction enthalpy.
- If the equation has a different stoichiometric coefficient than the one you want, multiply everything by the number to make it what you want, including the reaction enthalpy
Watch Video \(\PageIndex{1}\) to see these steps put into action while solving example \(\PageIndex{1}\).
Example \(\PageIndex{3}\) Calculating enthalpy of reaction with hess's law and combustion table
Using table \(\PageIndex{1}\) Calculate the enthalpy of reaction for the hydrogenation of ethene into ethane
\[C_2H_4 + H_2 \rightarrow C_2H_6 \nonumber \]
Solution
Hess's Law is a consequence of the first law, in that energy is conserved.
We want the enthalpy for the reaction
\[C_2H_4 + H_2 \rightarrow C_2H_6 \nonumber \]
From table \(\PageIndex{1}\) we obtain the following enthalpies of combustion
\[\begin{align} \text{eq. 1: } \; \; \; \; & H_2+1/2O_2 \rightarrow H_2O \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;\; \; \; \;\Delta H_1=-286 kJ/mol \nonumber \\ \text{eq. 2: } \; \; \; \; & C_2H_4 +3O_2 \rightarrow 2CO_2 + 2H_2O \; \; \; \; \; \; \; \; \Delta H_2= -1411 kJ/mol \nonumber \\ \text{eq. 3: } \; \; \; \; & C_2H_6+ 3/2O_2 \rightarrow 2CO_2 + 3H_2O \; \; \; \; \; \Delta H_3= -1560 kJ/mol \end{align}\]
Video \(\PageIndex{1}\) shows how to tackle this problem. The trick is to add the above equations to produce the equation you want. So, identify species that only exist in one of the given equations and put them on the desired side of the equation you want to produce, following the Tips above. Your final answer should be -131kJ/mol
Enthalpy as a State Function
What is important here, is that by measuring the heats of combustion scientists could acquire data that could then be used to predict the enthalpy of a reaction that they may not be able to directly measure. This is a consequence of enthalpy being a state function, and the path of the above three steps has the same energy change as the path for the direct hydrogenation of ethylene. We can look at this in an Energy Cycle Diagram (Figure \(\PageIndex{2}\)).
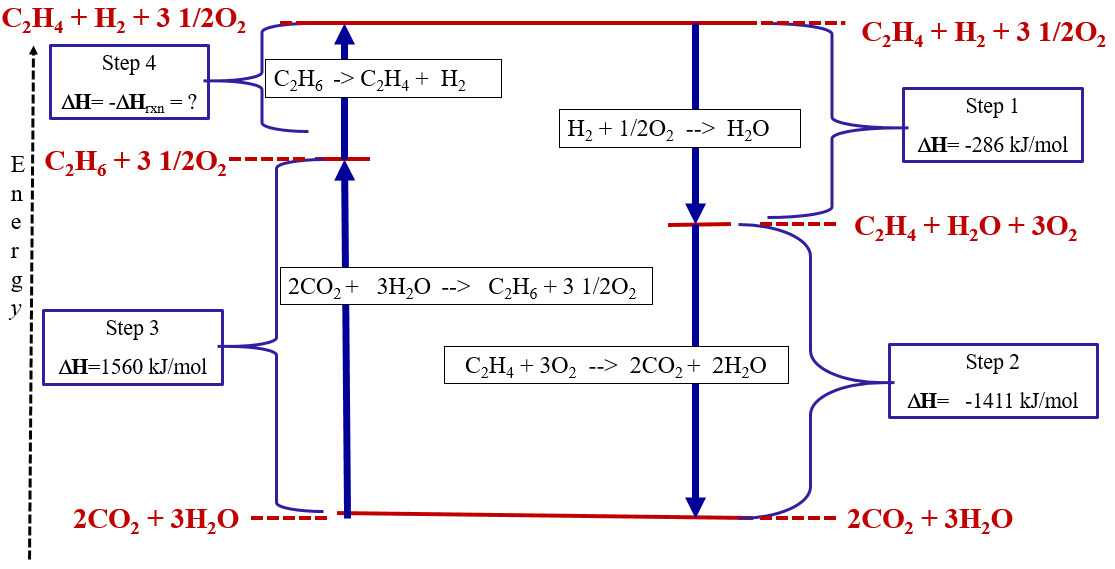
Figure \(\PageIndex{2}\): The steps of example \(\PageIndex{1}\) expressed as an energy cycle.
Because enthalpy is a state function, a process that involves a complete cycle where chemicals undergo reactions and are then reformed back into themselves, must have no change in enthalpy, meaning the endothermic steps must balance the exothermic steps.
\[\Delta H_1 +\Delta H_2 + \Delta H_3 + \Delta H_4 = 0\]
That is, the energy lost in the exothermic steps of the cycle must be regained in the endothermic steps, no matter what those steps are.
Exothermic Steps
- \(\Delta H_1\) = -296kJ/mol
- \(\Delta H_2\) = -1411kJ/mol Total Exothermic = -1697 kJ/mol
Endothermic Steps
- \(\Delta H_3\) = + 1560kJ/mol
- \(\Delta H_4\) = - \(\Delta H^*_{rxn}\) = ? J/mol Total Endothermic = + 1697 kJ/mol
Note, step 4 shows C2H6 -- > C2H4 +H2 and in example \(\PageIndex{1}\) we are solving for C2H4 +H2 --> C2H6 which is the reaction of step 4 written backwards, so the answer to \(\PageIndex{1}\) is the negative of step 4. This problem is solved in video \(\PageIndex{1}\) above.
Standard Enthalpies of Formation
The standard molar enthalpy of formation ΔHof is the enthalpy change when 1 mole of a pure substance, or a 1 M solute concentration in a solution, is formed from its elements in their most stable states under standard state conditions. In this class, the standard state is 1 bar and 25°C. Note, if two tables give substantially different values, you need to check the standard states. One of the values of enthalpies of formation is that we can use them and Hess's Law to calculate the enthalpy change for a reaction that is difficult to measure, or even dangerous. We can look at this as a two step process.
Note the enthalpy of formation is a molar function, so you can have non-integer coefficients. For example, the molar enthalpy of formation of water is:
\[H_2(g)+1/2O_2(g) \rightarrow H_2O(l) \; \; \Delta H_f^o = -285.8 \; kJ/mol \\ H_2(g)+1/2O_2(g) \rightarrow H_2O(g) \; \; \Delta H_f^o = -241.8 \; kJ/mol \]
This equation says that 85.8 kJ is of energy is exothermically released when one mole of liquid water is formed by reacting one mole of hydrogen gas and 1/2mol oxygen gas (3.011x1023 molecules of O2). Note, ΔHfo =of liquid water is less than that of gaseous water, which makes sense as you need to add energy to liquid water to boil it.
Table \(\PageIndex{2}\): Standard enthalpies of formation for select substances. A more comprehensive table can be found at the table of standard enthalpies of formation , which will open in a new window, and was taken from the CRC Handbook of Chemistry and Physics, 84 Edition (2004).
Example \(\PageIndex{4}\): Writing Reaction Equations for \(ΔH^\circ_\ce{f}\)
Write the heat of formation reaction equations for:
- \(\ce{C2H_5OH}_{(l)}\)
- \(\ce{Ca_3(PO_4)}_{2(s)}\)
Solution
Remembering that \(ΔH^\circ_\ce{f}\) reaction equations are for forming 1 mole of the compound from its constituent elements under standard conditions, we have:
- \(\ce{2C}(s,\:\ce{graphite})+\ce{3H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OH}(l)\)
- \(\ce{3Ca}(s)+\frac{1}{2}\ce{P4}(s)+\ce{4O2}(g)⟶\ce{Ca3(PO4)2}(s)\)
Note: The standard state of carbon is graphite, and phosphorus exists as \(P_4\).
Exercise \(\PageIndex{3}\)
Write the heat of formation reaction equations for:
- \(\ce{C_2H_5OC_2H}_{5(l)}\)
- \(\ce{Na_2CO}_{3(s)}\)
- Answer a
-
\(\ce{4C}(s,\:\ce{graphite})+\ce{5H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OC2H5}(l)\);
- Answer b
-
\(\ce{2Na}(s)+\ce{C}(s,\:\ce{graphite})+\dfrac{3}{2}\ce{O2}(g)⟶\ce{Na2CO3}(s)\)
Calculating Enthalpy of Reaction from Standard Enthalpies of Formation
Because enthalpy of reaction is a state function the energy change between reactants and products is independent of the path. We can choose a hypothetical two step path where the atoms in the reactants are broken into the standard state of their element (left side of Figure \(\PageIndex{3}\)), and then from this hypothetical state recombine to form the products (right side of Figure \(\PageIndex{3}\)). Note the first step is the opposite of the process for the standard state enthalpy of formation, and so we can use the negative of those chemical species's ΔHformation.
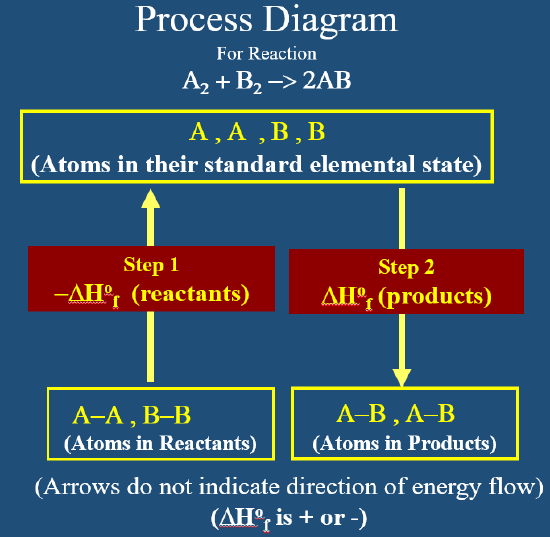
Note: Enthalpy vs. Molar Enthalpy
Enthalpy, qp, is an extensive property and for example the energy released in the combustion of two gallons of gasoline is twice that of one gallon. As such, enthalpy has the units of energy (typically J or cal). Molar enthalpies of formation are intensive properties and are the enthalpy per mole, that is the enthalpy change associated with the formation of one mole of a substance from its elements in their standard states. Thus molar enthalpies have units of kJ/mol or kcal/mol, and are tabulated in thermodynamic tables. Also not that the equations associated with molar enthalpies are per mole substance formed, and can thus have non-interger stoichiometric coeffiecents. That is, you can have half a mole (but you can not have half a molecule.
The molar enthalpy of reaction can be used to calculate the enthalpy of reaction if you have a balanced chemical equation. This is described by the following equation, where where mi and ni are the stoichiometric coefficients of the products and reactants respectively.
\[\Delta H_{reaction}=\sum m_i \Delta H_{f}^{o}(products) - \sum n_i \Delta H_{f}^{o}(reactants) \\ where \; m_i \; and \; n_i \; \text{are the stoichiometric coefficients of the products and reactants respectively} \]
If we look at the process diagram in Figure \(\PageIndex{3}\) and correlate it to the above equation we see two things.
- Reactants break apart into their atoms that take their elemental standard state forms. This is the opposite of forming them, so this step is the negative of their enthalpy of formation.
- Products form from their atoms in their elemental standard state forms. This is their enthalpy of formation
In both cases you need to multiply by the stoichiomertic coefficients to account for all the species in the balanced chemical equation. This allows us to use thermodynamic tables to calculate the enthalpies of reaction and although the enthalpy of reaction is given in units of energy (J, cal) we need to remember that it is related to the stoichiometric coefficient of each species (review section 5.5.2 enthalpies and chemical reactions ).
So the equation
\[\Delta H_{reaction}=\sum m_i \Delta H_{f}^{o}(products) - \sum n_i \Delta H_{f}^{o}(reactants) \nonumber \]
describes the enthalpy change as reactants break apart into their stable elemental state at standard conditions and then form new bonds as they create the products.
Let's apply this to the combustion of ethylene (the same problem we used combustion data for).
C2H4 + H2 --> C2H6
using the above equation, we get,
ΔHreaction = ΔHfo (C2H6) - ΔHfo (C2H4) - ΔHfo (H2)
ΔH -84 -(52.4) -0= -136.4 kJ
while above we got -136, noting these are correct to the first insignificant digit.
Example \(\PageIndex{5}\)
Calculate the enthalpy of formation for acetylene, C2H2(g) from the combustion data (table \(\PageIndex{1}\), note acetylene is not on the table) and then compare your answer to the value in table \(\PageIndex{2}\)
ΔHcomb (C2H2(g)) = -1300kJ/mol
ΔHcomb (C(s)) = -394kJ/mol
ΔHcomb (H2(g)) = -276kJ/mol
Note, in the following video we used Hess's Law to calculate the enthalpy for the balanced equation, with integer coefficients. It is important that students understand that ΔHreaction is for the entire equation, so in the case of acetylene, the balanced equation is
2C2H2(g) + 5O2(g) --> 4CO2(g) +2 H2O(l) ΔHreaction (C2H2) = -2600kJ
But when tabulating a molar enthaply of combustion, or a molar enthalpy of formation, it is per mole of the species being combusted or formed. That is, the equation in the video and the one above have the exact same value, just one is per mole, the other is per 2 mols of acetylene.
Solution
Watch the video below to get the tips on how to approach this problem.
Step 1: Write out each eq.
\[\begin{align} 2C_2H_2(g) + 5O_2(g) \rightarrow 4CO_2(g) + 2H_2O(l) \; \; \; \; \; \; & \Delta H_{comb} =-2600kJ \nonumber \\ C(s) + O_2(g) \rightarrow CO_2(g) \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; & \Delta H_{comb}= -393kJ \nonumber \\ 2H_2(g) + O_2 \rightarrow 2H_2O(l) \; \; \; \; \; \; \; \; \; \; \; \;\; \; \; \; \; \; & \Delta H_{comb} = -572kJ \end{align}\]
Step 2: Write out what you want to solve (eq. for the formation of C2H2).
\[ H_2(g) +2C(s) \rightarrow C_2H_2(g)\]
Step 3: Combine given eqs. so they add into desired eq.
- If you reverse Equation change sign of enthalpy
- if you multiply or divide by a number, multiply or divide the enthalpy by that number
\[\begin{align} \cancel{\color{red}{2CO_2(g)}} + \cancel{\color{green}{H_2O(l)}} \rightarrow C_2H_2(g) +\cancel{\color{blue} {5/2O_2(g)}} \; \; \; \; \; \; & \Delta H_{comb} = -(-\frac{-2600kJ}{2} ) \nonumber \\ \nonumber \\ 2C(s) + \cancel{\color{blue} {2O_2(g)}} \rightarrow \cancel{\color{red}{2CO_2(g)}} \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; & \Delta H_{comb}= 2(-393 kJ) \nonumber \\ \nonumber \\ H_2(g) +\cancel{\color{blue} {1/2O_2(g)}} \rightarrow \cancel{\color{green}{H_2O(l)}} \; \; \; \; \; \; \; \; \; \; \; & \Delta H_{comb} = \frac{-572kJ}{2} \end{align}\]
Step 4: Sum the Enthalpies: 226kJ (the value in the standard thermodynamic tables is 227kJ, which is the uncertain digit of this number)
See video \(\PageIndex{2}\) for tips and assistance in solving this.
Enthalpies of Reaction and Stoichiometric Problems
Example \(\PageIndex{5}\)
Determine the heat released or absorbed when 15.0g Al react with 30.0g Fe3O4(s).
Solution
There are three Tasks to this problem
- Balance Equation and Identify Limiting Reagent
- Calculate ΔHreaction from enthalpies of formation
- Calculate the heat given off by the complete consumption of the limiting reagent
Step 1: \[ \underset {15.0g \; Al \\ 26.98g/mol}{8Al(s)} + \underset {30.0 g \\ 231.54g/mol}{3Fe_3O_4(s)} \rightarrow 4Al_2O_3(s) + 9Fe(3)\]
\[15gAl\left(\frac{molAl}{26.98g}\right) \left(\frac{1}{8molAl}\right) = 0.069\]
\[30.0gFe_{3}O_{4}\left(\frac{1molFe_{3}O_{4}}{231.54g}\right) \left(\frac{1}{3molFe_{3}O_{4}}\right) = 0.043\]
So Fe3O4(s) is the limiting reagent.
Step 2:
From T1: Standard Thermodynamic Quantities we obtain the enthalpies of formation
| ΔHfo (Fe3O4) | ΔHfo (Al2O3) | ΔHfo (Al) | ΔHfo (Fe) |
| -1118.4kJ/mol | -1675.7kJ/mol | 0 | 0 |
Using
ΔHreaction = ∑mi ΔHfo (products)–∑ ni ΔHfo (reactants)
gives
ΔHreaction = 4(-1675.7) + 9(0) -8(0) -3(-1118.4)= -3363.6kJ
Step 3:
Base heat released on complete consumption of limiting reagent.
\[30.0gFe_{3}O_{4}\left(\frac{1molFe_{3}O_{4}}{231.54g}\right) \left(\frac{-3363kJ}{3molFe_{3}O_{4}}\right) = -145kJ\]
Note, you could have used the 0.043 from step 2,
0.043(-3363kJ)=-145kJ
Example \(\PageIndex{7}\)
Using enthalpies of formation from T1: Standard Thermodynamic Quantities calculate the heat released when 1.00 L of ethanol combustion.
Solution
See video \(\PageIndex{3}\)
Energy and Stoichiometry.
Pure ethanol has a density of 789g/L. Using the tables for enthalpy of formation, calculate the enthalpy of reaction for the combustion reaction of ethanol, and then calculate the heat released when 1.00 L of pure ethanol combusts.
Exercise \(\PageIndex{4}\)
How much heat is produced by the combustion of 125 g of acetylene?
- Answer
-
6.25 × 103 kJ
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Ronia Kattoum (UALR)
- Paul Flowers, et al. Open Stax (examples and exercises)
- anonymous


