5.5: Enthalpy Changes of Chemical Reactions
- Page ID
- 52110
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Recognize that breaking bonds requires energy, and making new bonds releases energy
- Assess if the overall bond making and breaking process results in net energy input or output leading to overall exothermic or endothermic reactions
- Define standard reaction enthalpy and relate to stoichiometric coefficients in a a balanced chemical reaction
- Calculate the heat produced/consumed in chemical reaction based on amount of a reactants and products using standard reaction enthalpy and vice versa
Enthalpy of Reaction
When a reaction occurs, bonds in reactants break, the atoms rearrange and new bonds form as the products are created. If the bond energies of the formed bonds are different than the bond energies of the broken bonds, then the energy of the reactants is not equal to the energy of the products, and energy is either absorbed or released into the surroundings. There are a few things to note.
- Breaking bonds always requires energy, and so it is endothermic.
- Forming bonds is the opposite of breaking, and so it is exothermic.
Because enthalpy is a state function, we can energetically view a reaction as taking place in two steps (as illustrated in Figure \(\PageIndex{1}\). The first step is the endothermic step of breaking the reactant bonds and the second is the exothermic step of making the product bonds. The energy change of the reaction can be viewed as the sum of these two steps, and results in two possibilities,
- The exothermic step (2) is greater than the endothermic step (1) and the reaction is exothermic.
- The endothermic step (1) is greater than the exothermic step (2) and the reaction is endothermic.
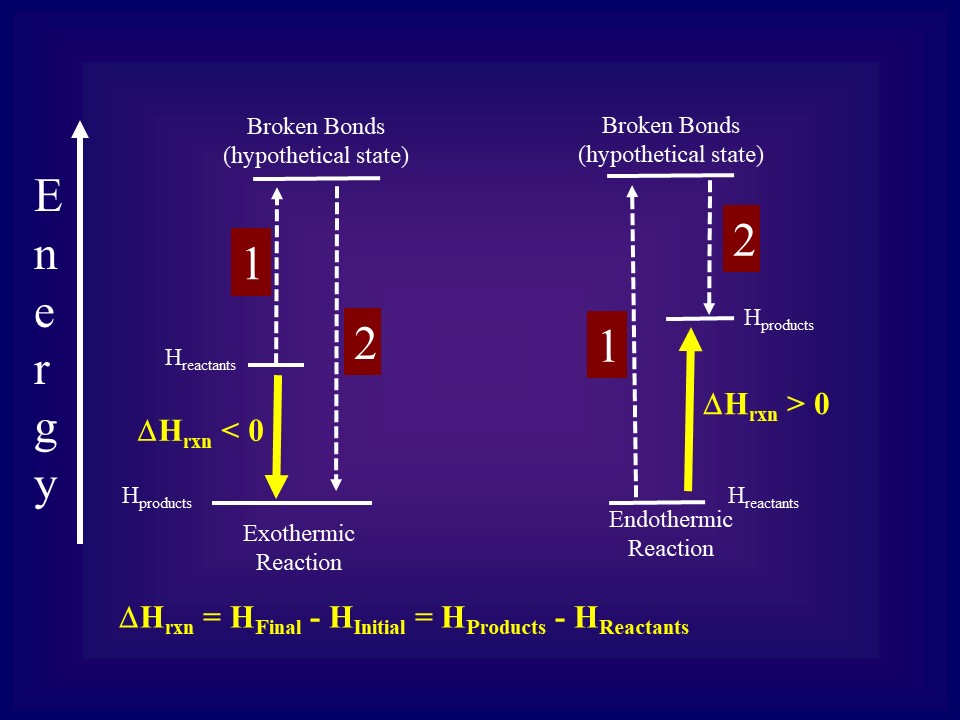
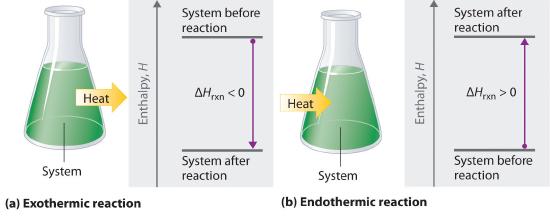
Note, we are interested in ΔH(reaction), which only depends on the initial (reactant) and final (product) state, because enthalpy is a state function this difference is path independent. What we do know is that the first step required energy and the second released energy. In Figure \(\PageIndex{2}\), we are only focusing on the energy difference between the initial and final states (yellow transition of Figure \(\PageIndex{1}\)).
Enthalpies of Reaction
In Chapter 3 (section 3.1) we learned about Lavoisier's "Law of Conservation of Matter", and from this we learned that chemical equation must be balanced. In the next Chapter 4, we applied stoichiometry to balanced equations and were able to predict reaction yields based on the complete consumption of the limiting reagent. In this section we are going to apply the First Law of Thermodynamics, the conservation of energy, to the balanced equation, and relate the energy of a chemical reaction to the stoichiometric coefficients of a reaction. The Enthalpy of Reaction is the energy evolved when the number of moles of each species is their coefficient, and this results in an equivalence statement that relates the stoichiometric number of each species to the enthalpy of reaction. The enthalpy of reaction is not written as per mole, but that information is implicit.
Enthalpy and Chemical Reactions
Endothermic Reactions: In endothermic reactions the heat is added to the system as reactants convert to products, and so the sign of ΔH is positive. Now the units of ΔHreaction often confuse students, as there are actually implicit units of mole in the denominator, where it is based on the stoichiometric coefficient of the chemical you are interested in. The easiest way to look at this is as an equivalence statement, where the enthalpy of reaction is related to the coefficient of each species.
Reactants + Heat → Products, ΔH>0
Example:
\[4CO_2(g)+2H_2O(l) \rightarrow 2C_2H_2(g)+ 5O_2(g) \; \; \;\Delta H_{reaction}=2599kJ \label{reaction}\]
The above equation is really saying 2599 kJ are being released for every 4 moles of CO2, 2 moles H2O, 2 moles C2H2 and 5 moles O2.
This gives four equivalence statements
4 mole CO2 = 2559kJ
2 mole H2O = 2559kJ
2 mole C2H2 = 2559kJ
5 mole O2 = 2559kJ
Example \(\PageIndex{1}\)
Calculate the energy released when 88.0g C2H2 react with excess oxygen according to the above equation
Solution
Note: C2H2 is a product and in so the above equation needs to be written backwards, which changes the sign from endothermic (+) to exothermic (-).
2C2H2(g)+5O2(g) → 4CO2(g)+2H2O(l) (ΔHreaction = -2599 kJ)
\[88.0g C_{2}H_{2} \left(\frac{ molC_{2}H_{2}}{26.0378g}\right) \left(\frac{-2559kJ}{2molC_{2}H_{2}}\right) = -4,324kJ\]
Exothermic reactions: In exothermic reactions heat is released from the system as reactants convert to products, and so the sign of ΔH is negative. Note, in example \(\PageIndex{1}\) 1 we wrote the endothermic reaction of \ref{reaction} backwards and it became exothermic. This is an important principle and a consequence of the First Law of Thermodynamics. That is, if a reaction is endothermic in one direction, it is exothermic in the other, and the amount of energy absorbed in the endothermic direction is equal to the amount released in the exothermic direction.
Reactants + Heat → Products + Heat, ΔH<0
Example:
\[2C_2H_2(g)+ 5O_2(g) \rightarrow 4CO_2(g)+2H_2O(l)\; \; \;\Delta H_{reaction}=-2599kJ \label{r2}\]
Looking at the energetics as a series of equivalence statements gives:
4 mole CO2 = -2559kJ
2 mole H2O = -2559kJ
2 mole C2H2 = -2559kJ
5 mole O2 = -2559kJ
Exercise \(\PageIndex{1}\)
According to Equation \ref{r2}, how much heat is evolved if 88.0 g of oxygen reacts with excess C2H2?
- Answer
-
\[88.0g O_{2}\left(\frac{ molO_{2}}{32.00g}\right) \left(\frac{-2559kJ}{5molO_{2}}\right) = -1,410kJ\]
Exercise \(\PageIndex{2}\)
Consider the following reaction:
\[\ce{CO + 2 H2 → CH3OH + 128 kJ} \nonumber\]
- Is the reaction endothermic or exothermic?
- If 12.2 g of hydrogen gas are reacted _______________kJ are ______________(produced/consumed).
- If 455 kJ of energy is produced, what was the mass of CO that was reacted?
- Answer a
-
Exothermic. Since the heat is written on the right side of the equation, it can be thought of as heat produced or generated. So, it is an exothermic reaction. This reaction can also be written in this format, where the enthalpy is represented as having a negative value.
- Answer b
-
387 kJ are produced:
- Answer c
-
99.6 grams of CO reacted:
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Ronia Kattoum (UALR)
- anonymous


