5.6: Calorimetry
- Page ID
- 52111
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Apply the First Law of Thermodynamics to calorimetry
- Compare heat flow from hot to cold objects in an ideal calorimeter versus a real calorimeter
- Calculate heat, temperature change, and specific heat after thermal equilibrium is reached between two substances in a calorimeter
- Calculate the molar heat of enthalpy for a reactions using coffee cup calorimetry
- Compare and contrast coffee cup calorimetry and bomb calorimetry
Calorimetry
Calorimetery is an application of the First Law of Thermodynamics to heat transfer, and allows us to measure the enthalpies of reaction or the heat capacities of substances. From the first law we can state
\[\Delta E_{Universe} = ΔE_{System} + ΔE_{Surrounding} = 0\]
therefore,
\[ ΔE_{System} = - ΔE_{Surrounding}\]
A calorimeter is an instrument that has a thermally isolated compartment that is designed to prevent heat flow to the surroundings. Technically, this is called an adiabatic surface in that no heat flows in and out of the calorimeter, which is in contrast to isothermal, which means constant temperature. In truth, there is no such thing as a thermally isolated system, but we can design systems that approach it on the time scale of a measurement. We will consider two types of calorimeters, ideal calorimeters, where the calorimeter does not absorb heat itself, and real calorimeters, where the calorimeter absorbs heat. We will apply calorimetry to two different thermodynamic processes, that of transference of heat across objects at different temperatures, and that released or absorbed by a chemical reaction. We will look at two ways of measuring this heat, either the temperature change of the calorimeter, or the mass of a substance that undergoes a phase change within the calorimeter at a constant temperature.
If we consider the work in a calorimeter to be zero, and noting that Δ E = Δ Q + W, the above equation becomes
\[\Delta Q_{system} = -\Delta Q_{Surrounding}\]
If we can measure the heat absorbed or lost by the surroundings we can use the above equivalence statement to calculate the heat lost or absorbed the system, and this is the basis for calorimetry. Figure \(\PageIndex{1}\) shows the basic layout of an ideal calorimeter where the gray shaded box acts as a surface that prevent any heat entering or leaving the solution, and so the solution functions as the surroundings. In the first exothermic process heat is released by the system and the temperature rises, while in the second endothermic process heat is absorbed by the system and the temperature decreases.
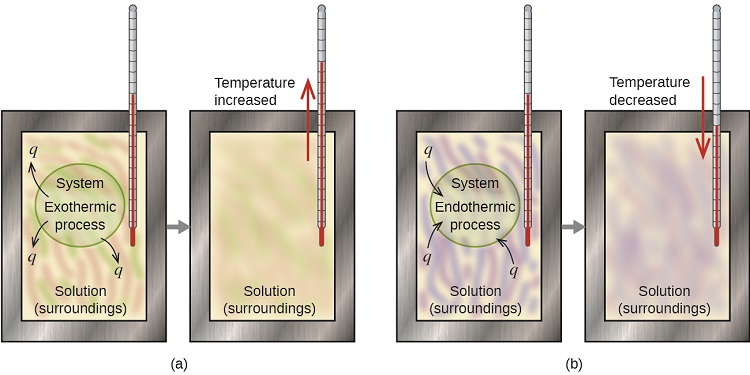
Heat Transfer Between Hot and Cold Objects in an Ideal Calorimeter
When a hot object (TH) is placed in thermal contact with a cold object (TC) energy is transferred between the two, but the rate of heat transfer from the hot to the cold is greater, so it cools down while the cold object heats up, until they reach the same temperature (TF). Once they are at the same temperature the system is at thermal equilibrium and the rate of transfer of energy from the hot to cold is the same as cold to hot. That is, energy is a vectoral flow, and even at the same temperature, there is a flow of energy across the boundary of two objects, but the flow is the same.
Starting with the first law for two isolated objects and considering no work, we have
\[q_{cold} + q_{hot}=0\]
so
\[q_{cold} =- q_{hot}=0\]
From section 5.2 we know that for a substance in a constant phase the heat relates to the temperature by equation 5.2.3 (q=mc\(\Delta|)T, which substituting into the above two equations give
\[ m_Cc_C \Delta T _C + m_Hc_H \Delta T_H=0 \]
or
\[ m_Cc_C \Delta T _C =- m_Hc_H \Delta T_H \]
where
\[\Delta T_H= T_F-T_H \; \; and \; \; \Delta T_C= T_F-T_C\]
In an ideal calorimeter we consider the calorimeter to absorb no heat itself, so if we have material of a uniform composition, we can relate the heat transferred from the hot object to the cold object by eq. 5.6.7.
Example \(\PageIndex{1}\) Ideal calorimeter problem
What is TF when 2.00g Au at 100.0°C is placed into 25.0 ml H2O at 30.0°C? You can obtain the specific heat capacities for gold and water from table 5.2.1.
Solution
You are solving 5.6.7 for \(T_F\).
\[T_F=\frac{m_Hc_HT_H+m_cc_cT_c}{m_Hc_H+m_cc_c} = 30.17^oC\]
The solution to this problem is worked out in video \(\PageIndex{1}\)
Heat Transfer Between Hot and Cold Objects in a Real Calorimeter
In a real calorimeter the calorimeter itself will absorb some of the heat, even if it transfers no heat to the surroundings. That is, the calorimeter itself has a heat capacitance. This usually needs to be measured for each calorimeter, and following the conventions of section 4.2, we use a capital C to represent the capacitance of an object, or the calorimeter constant. That is, the calorimeter constant is the calorimeter's heat capacitance.
Consider dropping a hot object into cold water that has been sitting in a calorimeter long enough to have the same temperature as the calorimeter.
From eq. 5.6 we know that QCold = -QHot ,
But now there are two cold objects, the water and the calorimeter, so
\[Q_c=m_cc_c \Delta T_c + C_{cal} \Delta T_c\]
where Ccal is the heat capacitance of the calorimeter.
Exercise \(\PageIndex{1}\)
Example \(\PageIndex{2}\) (below) is the same problem as Example \(\PageIndex{1}\) (above) but it is in a real calorimeter. Do you think TF in a real calorimeter will be hotter or colder than in the ideal?
- Answer
-
It will be colder because in example \(\PageIndex{1}\) the 2 g Au was transferring its heat to 25 mL water, while in example \(\PageIndex{2}\) it is transferring the heat to 25 mL of water AND the calorimeter itself.
is the same problem as Example \(\PageIndex{1}\) but it is in a real calorimeter. Before solving this or looking at the answer,
Example \(\PageIndex{2}\) Real calorimeter problem
What is TF when 2.00g Au at 100.0°C is placed into 25.0 ml H2O at 30.0°C? The calorimeter constant for the calorimeter is 36.0 J/°C and you can obtain the specific heat capacities for gold and water from table 5.2.1.
Solution
You are solving eq. 5.6.10 for \(T_F\), but there are two entities absorbing the heat
\[ Q_c +Q_H=0 \\ (m_cc_c \Delta T _c + C_{cal} \Delta T _C) + m_Hc_H \Delta T_H=0 \]
\[ T_F=\frac{m_Hc_HT_H+\left ( m_cc_c +C_{cal}\right )T_c}{m_Hc_H+C_{cal} + m_cc_c} = 30.12^oC \]
The solution to this problem is worked out in video \(\PageIndex{2}\) below.
Exercise \(\PageIndex{2}\)
Calculate the calorimeter constant if 150.0 g of lead at 100.0°C were placed in a calorimeter with 50.0 g of water at 22.0°C and the resulting temperature of the mixture was 26.2°C, you can obtain the specific heat capacities for lead and water from table 5.2.1.
- Answer
-
As in example \(\PageIndex{2}\), we start with the first law (for a system that does no work).
\[ Q_c +Q_H=0 \\ (m_cc_c \Delta T _c + C_{cal} \Delta T _C) + m_Hc_H \Delta T_H=0 \]
solve for Ccal.
\[c_{cal}=\frac{m_cc_c \Delta T _c + m_Hc_H \Delta T_H}{\Delta T_c} \\ =\frac{50.0g\left ( 4.184\frac{J}{g^oC} \right )\left ( 4.2^oC \right )+ 150.0g\left (0.128 \frac{J}{g^oC} \right )\left ( -73.8^oC \right )}{4.2^oC}=550J\]
Calorimetry and Enthalpies of Reaction
Calorimeters can also measure the molar enthalpy of reaction, by simply equating the heat absorbed/lost by the calorimeter to the heat lost/absorbed by the reaction. That is, the system is the reaction. To come up with the heat of reaction, you need to know what the limiting reagent is, and calculate it from that.
Starting with the first law and considering there to be no work
\[Q_{system}=-Q_{surrounding} \\\text{which becomes} \\ Q_{reaction}=-Q_{calorimeter}\]
- Qcalorimeter represents the calorimeter and everything in it. That is, all the heat exchanged with the reaction is absorbed or released by the calorimeter and its contents.
- Qreaction is the enthalpy of reaction (\(\Delta H_{r}\)) for a system at constant pressure. If we know the moles of the limiting reagent, we can divide by that and come up with the molar enthalpy of reaction
The following example shows how to calculate the molar enthalpy of reaction for the reaction between sulfuric acid and sodium hydroxide.
Example \(\PageIndex{3}\)
Calculate \(\Delta H_r\) for the neutralization of sodium hydroxide by sulfuric acid if 100.0 mL of 1.00M H2SO4 reacts with 100.0mL of 1.00M NaOH if all reactants were at 25.0oC before reaction and reached a final temperature of 32.0oC after the reaction. Treat the solutions as if they had the same specific heat capacity and density of pure water,
Solution
Step 1: Identify limiting reagent so we can identify moles reacted.
\[\underset{V=100.0mL\\M=1.00M}{H_2SO_4}+ \underset{100.0mL \\M=1.00M}{2NaOH} \rightarrow Na_2SO_4 + 2H_2O\]
Sodium hydroxide (NaOH) is the limiting reagents (calculate moles of each reactant and divide by stoichiometric coefficient, review section 4.2 in necessary)
\[n_{NaOH}=1.00\frac{molNaOH}{L}\left ( 0.1000L \right )=0.100mol \;NaOH\]
Step 2: Calculate heat of reaction based on the first law of thermodynamics
We note the heat transferred from the reaction is abosorbed by the calorimeter and its contents, noting that the calorimeter itself is ideal and so its calorimeter constant is zero (Ccal=0).
\[\begin{align}Q_R & =-Q_{calorimeter} \nonumber \\ & = -m_{contents}c_{H_2O}\Delta T \nonumber \\ & = -200.0g\left ( 4.184\frac{J}{g^oC} \right )\left ( 32.0^oC-25.0^oC \right ) \nonumber \\ &= -5.9kJ \end{align}\]
Step 3: Relate this to the moles of the limiting reagent
You know know that when 0.1000 M of NaOH completely reacted that -59.kJ of heat was released, so use the stoichiometric equation to calculate the heat of reaction.
\[\frac{\Delta H_{r}}{mol \; NaOH}= \frac{-5.9kJ}{0.100mol} = -59kJ/mol \; NaOH\]
Step 4: Relate this to the balanced equation to get the enthalpy of reaction
Remember, the enthalpy of reaction is the energy related to the balanced equation, not each reactant or product. So for the neutralization fo sulfuric acid by sodium hydroxide it is per mole sulfuric acid consumed, per 2 moles sodium hydroxide consumed, per mole sodium sulfate produced and per two moles sodium chloride produced.
So
\[\Delta H_{reaction} = -59 \frac{kJ}{mol \;NaOH}(2 \; mol \; NaOH)= -120kJ\]
Lets do a quick review of what the enthalpy of reaction means. So for the reaction
H2SO4(aq) + 2NaOH(aq) --> Na2SO4(aq) + 2 NaCl
it means is that for each mole of H2SO4 consumed or Na2SO4 produced- 120kJ of energy is released, while for each mole of NaOH consumed or NaCl produced -59kJ of energy is released when sodium hydroxide reacts with sulfuric acid.
Constant-Volume Calorimetry: Combustion Data
Constant-pressure calorimeters are not very well suited for studying reactions in which one or more of the reactants is a gas, such as a combustion reaction. The enthalpy changes that accompany combustion reactions are therefore measured using a constant-volume calorimeter, such as the bomb calorimeter(A device used to measure energy changes in chemical processes. shown schematically in Figure \(\PageIndex{3}\)). The reactant is placed in a steel cup inside a steel vessel with a fixed volume (the “bomb”). The bomb is then sealed, filled with excess oxygen gas, and placed inside an insulated container that holds a known amount of water. Because combustion reactions are exothermic, the temperature of the bath and the calorimeter increases during combustion. If the heat capacity of the bomb and the mass of water are known, the heat released can be calculated.

Because the volume of the system (the inside of the bomb) is fixed, the combustion reaction occurs under conditions in which the volume, but not the pressure, is constant. The heat released by a reaction carried out at constant volume is identical to the change in internal energy (\(ΔU\)) rather than the enthalpy change (\(ΔH\)); \(ΔU\) is related to \(ΔH\) by an expression that depends on the change in the number of moles of gas during the reaction. The difference between the heat flow measured at constant volume and the enthalpy change is usually quite small, however (on the order of a few percent). Assuming that \(ΔU < ΔH\), the relationship between the measured temperature change and \(ΔH_{comb}\) is given in Equation \(\ref{5.5.9}\), where Cbomb is the total heat capacity of the steel bomb and the water surrounding it:
\[ \Delta H_{comb} < q_{comb} = q_{calorimater} = C_{bomb} \Delta T \label{5.5.9}\]
To measure the heat capacity of the calorimeter, we first burn a carefully weighed mass of a standard compound whose enthalpy of combustion is accurately known. Benzoic acid (\(\ce{C6H5CO2H}\)) is often used for this purpose because it is a crystalline solid that can be obtained in high purity. The combustion of benzoic acid in a bomb calorimeter releases 26.38 kJ of heat per gram (i.e., its \(ΔH_{comb} = −26.38\, kJ/g\)). This value and the measured increase in temperature of the calorimeter can be used in Equation \(\ref{5.5.9}\) to determine \(C_{bomb}\). The use of a bomb calorimeter to measure the \(ΔH_{comb}\) of a substance is illustrated in Example \(\PageIndex{4}\).
Example \(\PageIndex{4}\): Combustion of Glucose
The combustion of 0.579 g of benzoic acid in a bomb calorimeter caused a 2.08 °C increase in the temperature of the calorimeter. The chamber was then emptied and recharged with 1.732 g of glucose and excess oxygen. Ignition of the glucose resulted in a temperature increase of 3.64°C. What is the \(ΔH_{comb}\) of glucose?
Given: mass and \(ΔT\) for combustion of standard and sample
Asked for: \(ΔH_{comb}\) of glucose
Strategy:
- Calculate the value of \(q_{rxn}\) for benzoic acid by multiplying the mass of benzoic acid by its \(ΔH_{comb}\). Then use Equation 5.6.21 to determine the heat capacity of the calorimeter (\(C_{bomb}\)) from \(q_{comb}\) and \(ΔT\).
- Calculate the amount of heat released during the combustion of glucose by multiplying the heat capacity of the bomb by the temperature change. Determine the ΔHcomb of glucose by multiplying the amount of heat released per gram by the molar mass of glucose.
Solution:
The first step is to use Equation \(\ref{5.5.9}\) and the information obtained from the combustion of benzoic acid to calculate Cbomb. We are given \(ΔT\), and we can calculate qcomb from the mass of benzoic acid:
\[ \begin{align*} q_{comb} &= \left ( 0.579 \; \cancel{g} \right )\left ( -26.38 \; kJ/\cancel{g} \right ) \\[4pt] &= - 15.3 \; kJ \end{align*} \]
From Equation \(\ref{5.5.9}\),
\[ \begin{align*} -C_{bomb} &= \dfrac{q_{comb}}{\Delta T} \\[4pt] &= \dfrac{-15.3 \; kJ}{2.08 \; ^{o}C} \\[4pt] &=- 7.34 \; kJ/^{o}C \end{align*} \]
B According to the strategy, we can now use the heat capacity of the bomb to calculate the amount of heat released during the combustion of glucose:
\[ \begin{align*} q_{comb} &=-C_{bomb}\Delta T \\[4pt] &= \left ( -7.34 \; kJ/^{o}C \right )\left ( 3.64 \; ^{o}C \right ) \\[4pt] &=- 26.7 \; kJ \end{align*} \]
Because the combustion of 1.732 g of glucose released 26.7 kJ of energy, the ΔHcomb of glucose is
\[ \begin{align*} \Delta H_{comb} &=\left ( \dfrac{-26.7 \; kJ}{1.732 \; \cancel{g}} \right )\left ( \dfrac{180.16 \; \cancel{g}}{mol} \right ) \\[4pt] &= -2780 \; kJ/mol \\[4pt] &=2.78 \times 10^{3} \; J/mol \end{align*} \]
This result is in good agreement (< 1% error) with the value of \(ΔH_{comb} = −2803\, kJ/mol\) that calculated using enthalpies of formation.
Exercise \(\PageIndex{4}\): Combustion of Benzoic Acid
When 2.123 g of benzoic acid is ignited in a bomb calorimeter, a temperature increase of 4.75 °C is observed. When 1.932 g of methylhydrazine (CH3NHNH2) is ignited in the same calorimeter, the temperature increase is 4.64 °C. Calculate the ΔHcomb of methylhydrazine, the fuel used in the maneuvering jets of the US space shuttle.
- Answer
-
−1.30 × 103 kJ/mol
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Ronia Kattoum
- anonymous


