5.4: Linear Regression and Calibration Curves
- Page ID
- 220691
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In a single-point external standardization we determine the value of kA by measuring the signal for a single standard that contains a known concentration of analyte. Using this value of kA and our sample’s signal, we then calculate the concentration of analyte in our sample (see Example 5.3.1). With only a single determination of kA, a quantitative analysis using a single-point external standardization is straightforward.
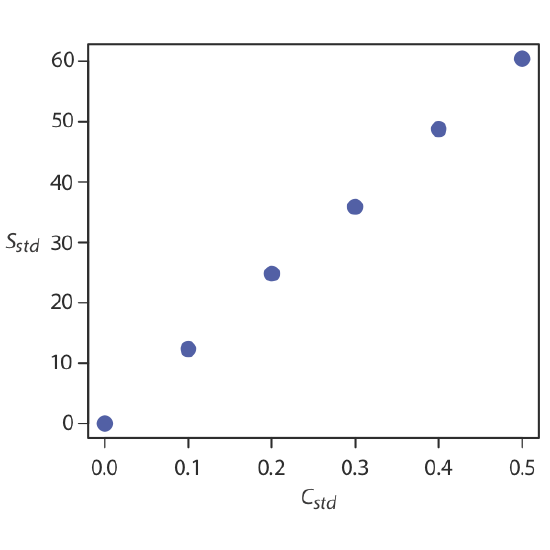
A multiple-point standardization presents a more difficult problem. Consider the data in Table \(\PageIndex{1}\) for a multiple-point external standardization. What is our best estimate of the relationship between Sstd and Cstd? It is tempting to treat this data as five separate single-point standardizations, determining kA for each standard, and reporting the mean value for the five trials. Despite it simplicity, this is not an appropriate way to treat a multiple-point standardization.
| \(C_{std}\) (arbitrary units) | \(S_{std}\) (arbitrary units) | \(k_A = S_{std}/C_{std}\) |
|---|---|---|
| 0.000 | 0.00 | — |
| 0.100 | 12.36 | 123.6 |
| 0.200 | 24.83 | 124.2 |
| 0.300 | 35.91 | 119.7 |
| 0.400 | 48.79 | 122.0 |
| 0.500 | 60.42 | 122.8 |
| mean kA = 122.5 |
So why is it inappropriate to calculate an average value for kA using the data in Table \(\PageIndex{1}\)? In a single-point standardization we assume that the reagent blank (the first row in Table \(\PageIndex{1}\)) corrects for all constant sources of determinate error. If this is not the case, then the value of kA from a single-point standardization has a constant determinate error. Table \(\PageIndex{2}\) demonstrates how an uncorrected constant error affects our determination of kA. The first three columns show the concentration of analyte in a set of standards, Cstd, the signal without any source of constant error, Sstd, and the actual value of kA for five standards. As we expect, the value of kA is the same for each standard. In the fourth column we add a constant determinate error of +0.50 to the signals, (Sstd)e. The last column contains the corresponding apparent values of kA. Note that we obtain a different value of kA for each standard and that each apparent kA is greater than the true value.
| \(C_{std}\) |
\(S_{std}\) |
\(k_A = S_{std}/C_{std}\) |
\((S_{std})_e\) |
\(k_A = (S_{std})_e/C_{std}\) |
|---|---|---|---|---|
| 1.00 | 1.00 | 1.00 | 1.50 | 1.50 |
| 2.00 | 2.00 | 1.00 | 2.50 | 1.25 |
| 3.00 | 3.00 | 1.00 | 3.50 | 1.17 |
| 4.00 | 4.00 | 1.00 | 4.50 | 1.13 |
| 5.00 | 5.00 | 1.00 | 5.50 | 1.10 |
| mean kA (true) = 1.00 | mean kA (apparent) = 1.23 |
How do we find the best estimate for the relationship between the signal and the concentration of analyte in a multiple-point standardization? Figure \(\PageIndex{1}\) shows the data in Table \(\PageIndex{1}\) plotted as a normal calibration curve. Although the data certainly appear to fall along a straight line, the actual calibration curve is not intuitively obvious. The process of determining the best equation for the calibration curve is called linear regression.
Linear Regression of Straight Line Calibration Curves
When a calibration curve is a straight-line, we represent it using the following mathematical equation
\[y = \beta_0 + \beta_1 x \label{5.1}\]
where y is the analyte’s signal, Sstd, and x is the analyte’s concentration, Cstd. The constants \(\beta_0\) and \(\beta_1\) are, respectively, the calibration curve’s expected y-intercept and its expected slope. Because of uncertainty in our measurements, the best we can do is to estimate values for \(\beta_0\) and \(\beta_1\), which we represent as b0 and b1. The goal of a linear regression analysis is to determine the best estimates for b0 and b1. How we do this depends on the uncertainty in our measurements.
Unweighted Linear Regression with Errors in y
The most common method for completing the linear regression for Equation \ref{5.1} makes three assumptions:
- that the difference between our experimental data and the calculated regression line is the result of indeterminate errors that affect y
- that indeterminate errors that affect y are normally distributed
- that the indeterminate errors in y are independent of the value of x
Because we assume that the indeterminate errors are the same for all standards, each standard contributes equally in our estimate of the slope and the y-intercept. For this reason the result is considered an unweighted linear regression.
The second assumption generally is true because of the central limit theorem, which we considered in Chapter 4. The validity of the two remaining assumptions is less obvious and you should evaluate them before you accept the results of a linear regression. In particular the first assumption always is suspect because there certainly is some indeterminate error in the measurement of x. When we prepare a calibration curve, however, it is not unusual to find that the uncertainty in the signal, Sstd, is significantly larger than the uncertainty in the analyte’s concentration, Cstd. In such circumstances the first assumption is usually reasonable.
How a Linear Regression Works
To understand the logic of a linear regression consider the example shown in Figure \(\PageIndex{2}\), which shows three data points and two possible straight-lines that might reasonably explain the data. How do we decide how well these straight-lines fit the data, and how do we determine the best straight-line?
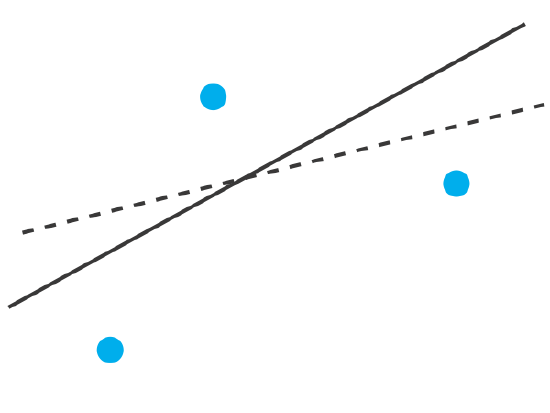
Let’s focus on the solid line in Figure \(\PageIndex{2}\). The equation for this line is
\[\hat{y} = b_0 + b_1 x \label{5.2}\]
where b0 and b1 are estimates for the y-intercept and the slope, and \(\hat{y}\) is the predicted value of y for any value of x. Because we assume that all uncertainty is the result of indeterminate errors in y, the difference between y and \(\hat{y}\) for each value of x is the residual error, r, in our mathematical model.
\[r_i = (y_i - \hat{y}_i) \nonumber\]
Figure \(\PageIndex{3}\) shows the residual errors for the three data points. The smaller the total residual error, R, which we define as
\[R = \sum_{i = 1}^{n} (y_i - \hat{y}_i)^2 \label{5.3}\]
the better the fit between the straight-line and the data. In a linear regression analysis, we seek values of b0 and b1 that give the smallest total residual error.
The reason for squaring the individual residual errors is to prevent a positive residual error from canceling out a negative residual error. You have seen this before in the equations for the sample and population standard deviations. You also can see from this equation why a linear regression is sometimes called the method of least squares.

Finding the Slope and y-Intercept
Although we will not formally develop the mathematical equations for a linear regression analysis, you can find the derivations in many standard statistical texts [ See, for example, Draper, N. R.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley: New York, 1998]. The resulting equation for the slope, b1, is
\[b_1 = \frac {n \sum_{i = 1}^{n} x_i y_i - \sum_{i = 1}^{n} x_i \sum_{i = 1}^{n} y_i} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2} \label{5.4}\]
and the equation for the y-intercept, b0, is
\[b_0 = \frac {\sum_{i = 1}^{n} y_i - b_1 \sum_{i = 1}^{n} x_i} {n} \label{5.5}\]
Although Equation \ref{5.4} and Equation \ref{5.5} appear formidable, it is necessary only to evaluate the following four summations
\[\sum_{i = 1}^{n} x_i \quad \sum_{i = 1}^{n} y_i \quad \sum_{i = 1}^{n} x_i y_i \quad \sum_{i = 1}^{n} x_i^2 \nonumber\]
Many calculators, spreadsheets, and other statistical software packages are capable of performing a linear regression analysis based on this model. To save time and to avoid tedious calculations, learn how to use one of these tools (and see Section 5.6 for details on completing a linear regression analysis using Excel and R.). For illustrative purposes the necessary calculations are shown in detail in the following example.
Equation \ref{5.4} and Equation \ref{5.5} are written in terms of the general variables x and y. As you work through this example, remember that x corresponds to Cstd, and that y corresponds to Sstd.
Using the data from Table \(\PageIndex{1}\), determine the relationship between Sstd and Cstd using an unweighted linear regression.
Solution
We begin by setting up a table to help us organize the calculation.
| \(x_i\) | \(y_i\) | \(x_i y_i\) | \(x_i^2\) |
|---|---|---|---|
| 0.000 | 0.00 | 0.000 | 0.000 |
| 0.100 | 12.36 | 1.236 | 0.010 |
| 0.200 | 24.83 | 4.966 | 0.040 |
| 0.300 | 35.91 | 10.773 | 0.090 |
| 0.400 | 48.79 | 19.516 | 0.160 |
| 0.500 | 60.42 | 30.210 | 0.250 |
Adding the values in each column gives
\[\sum_{i = 1}^{n} x_i = 1.500 \quad \sum_{i = 1}^{n} y_i = 182.31 \quad \sum_{i = 1}^{n} x_i y_i = 66.701 \quad \sum_{i = 1}^{n} x_i^2 = 0.550 \nonumber\]
Substituting these values into Equation \ref{5.4} and Equation \ref{5.5}, we find that the slope and the y-intercept are
\[b_1 = \frac {(6 \times 66.701) - (1.500 \times 182.31)} {(6 \times 0.550) - (1.500)^2} = 120.706 \approx 120.71 \nonumber\]
\[b_0 = \frac {182.31 - (120.706 \times 1.500)} {6} = 0.209 \approx 0.21 \nonumber\]
The relationship between the signal and the analyte, therefore, is
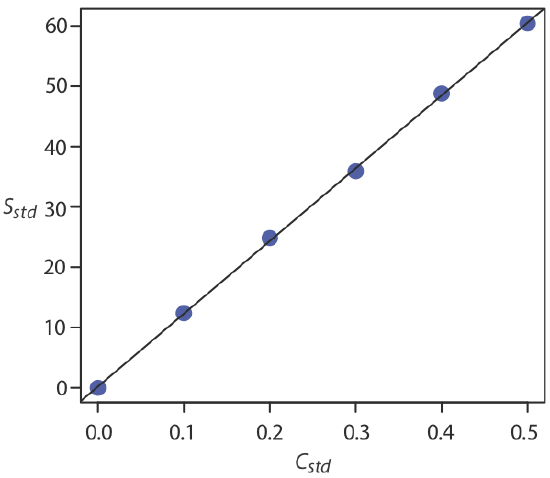
\[S_{std} = 120.71 \times C_{std} + 0.21 \nonumber\]
For now we keep two decimal places to match the number of decimal places in the signal. The resulting calibration curve is shown in Figure \(\PageIndex{4}\).
Uncertainty in the Regression Analysis
As shown in Figure \(\PageIndex{4}\), because indeterminate errors in the signal, the regression line may not pass through the exact center of each data point. The cumulative deviation of our data from the regression line—that is, the total residual error—is proportional to the uncertainty in the regression. We call this uncertainty the standard deviation about the regression, sr, which is equal to
\[s_r = \sqrt{\frac {\sum_{i = 1}^{n} \left( y_i - \hat{y}_i \right)^2} {n - 2}} \label{5.6}\]
where yi is the ith experimental value, and \(\hat{y}_i\) is the corresponding value predicted by the regression line in Equation \ref{5.2}. Note that the denominator of Equation \ref{5.6} indicates that our regression analysis has n – 2 degrees of freedom—we lose two degree of freedom because we use two parameters, the slope and the y-intercept, to calculate \(\hat{y}_i\).
Did you notice the similarity between the standard deviation about the regression (Equation \ref{5.6}) and the standard deviation for a sample (Equation 4.1.1)?
A more useful representation of the uncertainty in our regression analysis is to consider the effect of indeterminate errors on the slope, b1, and the y-intercept, b0, which we express as standard deviations.
\[s_{b_1} = \sqrt{\frac {n s_r^2} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2}} = \sqrt{\frac {s_r^2} {\sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \label{5.7}\]
\[s_{b_0} = \sqrt{\frac {s_r^2 \sum_{i = 1}^{n} x_i^2} {n \sum_{i = 1}^{n} x_i^2 - \left( \sum_{i = 1}^{n} x_i \right)^2}} = \sqrt{\frac {s_r^2 \sum_{i = 1}^{n} x_i^2} {n \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \label{5.8}\]
We use these standard deviations to establish confidence intervals for the expected slope, \(\beta_1\), and the expected y-intercept, \(\beta_0\)
\[\beta_1 = b_1 \pm t s_{b_1} \label{5.9}\]
\[\beta_0 = b_0 \pm t s_{b_0} \label{5.10}\]
where we select t for a significance level of \(\alpha\) and for n – 2 degrees of freedom. Note that Equation \ref{5.9} and Equation \ref{5.10} do not contain a factor of \((\sqrt{n})^{-1}\) because the confidence interval is based on a single regression line.
Calculate the 95% confidence intervals for the slope and y-intercept from Example \(\PageIndex{1}\).
Solution
We begin by calculating the standard deviation about the regression. To do this we must calculate the predicted signals, \(\hat{y}_i\) , using the slope and y-intercept from Example \(\PageIndex{1}\), and the squares of the residual error, \((y_i - \hat{y}_i)^2\). Using the last standard as an example, we find that the predicted signal is
\[\hat{y}_6 = b_0 + b_1 x_6 = 0.209 + (120.706 \times 0.500) = 60.562 \nonumber\]
and that the square of the residual error is
\[(y_i - \hat{y}_i)^2 = (60.42 - 60.562)^2 = 0.2016 \approx 0.202 \nonumber\]
The following table displays the results for all six solutions.
| \(x_i\) | \(y_i\) | \(\hat{y}_i\) |
\(\left( y_i - \hat{y}_i \right)^2\) |
|---|---|---|---|
| 0.000 | 0.00 | 0.209 | 0.0437 |
| 0.100 | 12.36 | 12.280 | 0.0064 |
| 0.200 | 24.83 | 24.350 | 0.2304 |
| 0.300 | 35.91 | 36.421 | 0.2611 |
| 0.400 | 48.79 | 48.491 | 0.0894 |
| 0.500 | 60.42 | 60.562 | 0.0202 |
Adding together the data in the last column gives the numerator of Equation \ref{5.6} as 0.6512; thus, the standard deviation about the regression is
\[s_r = \sqrt{\frac {0.6512} {6 - 2}} = 0.4035 \nonumber\]
Next we calculate the standard deviations for the slope and the y-intercept using Equation \ref{5.7} and Equation \ref{5.8}. The values for the summation terms are from Example \(\PageIndex{1}\).
\[s_{b_1} = \sqrt{\frac {6 \times (0.4035)^2} {(6 \times 0.550) - (1.500)^2}} = 0.965 \nonumber\]
\[s_{b_0} = \sqrt{\frac {(0.4035)^2 \times 0.550} {(6 \times 0.550) - (1.500)^2}} = 0.292 \nonumber\]
Finally, the 95% confidence intervals (\(\alpha = 0.05\), 4 degrees of freedom) for the slope and y-intercept are
\[\beta_1 = b_1 \pm ts_{b_1} = 120.706 \pm (2.78 \times 0.965) = 120.7 \pm 2.7 \nonumber\]
\[\beta_0 = b_0 \pm ts_{b_0} = 0.209 \pm (2.78 \times 0.292) = 0.2 \pm 0.80 \nonumber\]
where t(0.05, 4) from Appendix 4 is 2.78. The standard deviation about the regression, sr, suggests that the signal, Sstd, is precise to one decimal place. For this reason we report the slope and the y-intercept to a single decimal place.
Minimizing Uncertainty in Calibration Model
To minimize the uncertainty in a calibration curve’s slope and y-intercept, we evenly space our standards over a wide range of analyte concentrations. A close examination of Equation \ref{5.7} and Equation \ref{5.8} help us appreciate why this is true. The denominators of both equations include the term \(\sum_{i = 1}^{n} (x_i - \overline{x}_i)^2\). The larger the value of this term—which we accomplish by increasing the range of x around its mean value—the smaller the standard deviations in the slope and the y-intercept. Furthermore, to minimize the uncertainty in the y-intercept, it helps to decrease the value of the term \(\sum_{i = 1}^{n} x_i\) in Equation \ref{5.8}, which we accomplish by including standards for lower concentrations of the analyte.
Obtaining the Analyte's Concentration From a Regression Equation
Once we have our regression equation, it is easy to determine the concentration of analyte in a sample. When we use a normal calibration curve, for example, we measure the signal for our sample, Ssamp, and calculate the analyte’s concentration, CA, using the regression equation.
\[C_A = \frac {S_{samp} - b_0} {b_1} \label{5.11}\]
What is less obvious is how to report a confidence interval for CA that expresses the uncertainty in our analysis. To calculate a confidence interval we need to know the standard deviation in the analyte’s concentration, \(s_{C_A}\), which is given by the following equation
\[s_{C_A} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{S}_{samp} - \overline{S}_{std} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( C_{std_i} - \overline{C}_{std} \right)^2}} \label{5.12}\]
where m is the number of replicate we use to establish the sample’s average signal, Ssamp, n is the number of calibration standards, Sstd is the average signal for the calibration standards, and \(C_{std_1}\) and \(\overline{C}_{std}\) are the individual and the mean concentrations for the calibration standards. Knowing the value of \(s_{C_A}\), the confidence interval for the analyte’s concentration is
\[\mu_{C_A} = C_A \pm t s_{C_A} \nonumber\]
where \(\mu_{C_A}\) is the expected value of CA in the absence of determinate errors, and with the value of t is based on the desired level of confidence and n – 2 degrees of freedom.
Equation \ref{5.12} is written in terms of a calibration experiment. A more general form of the equation, written in terms of x and y, is given here.
\[s_{x} = \frac {s_r} {b_1} \sqrt{\frac {1} {m} + \frac {1} {n} + \frac {\left( \overline{Y} - \overline{y} \right)^2} {(b_1)^2 \sum_{i = 1}^{n} \left( x_i - \overline{x} \right)^2}} \nonumber\]
A close examination of Equation \ref{5.12} should convince you that the uncertainty in CA is smallest when the sample’s average signal, \(\overline{S}_{samp}\), is equal to the average signal for the standards, \(\overline{S}_{std}\). When practical, you should plan your calibration curve so that Ssamp falls in the middle of the calibration curve. For more information about these regression equations see (a) Miller, J. N. Analyst 1991, 116, 3–14; (b) Sharaf, M. A.; Illman, D. L.; Kowalski, B. R. Chemometrics, Wiley-Interscience: New York, 1986, pp. 126-127; (c) Analytical Methods Committee “Uncertainties in concentrations estimated from calibration experiments,” AMC Technical Brief, March 2006.
Three replicate analyses for a sample that contains an unknown concentration of analyte, yield values for Ssamp of 29.32, 29.16 and 29.51 (arbitrary units). Using the results from Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\), determine the analyte’s concentration, CA, and its 95% confidence interval.
Solution
The average signal, \(\overline{S}_{samp}\), is 29.33, which, using Equation \ref{5.11} and the slope and the y-intercept from Example \(\PageIndex{1}\), gives the analyte’s concentration as
\[C_A = \frac {\overline{S}_{samp} - b_0} {b_1} = \frac {29.33 - 0.209} {120.706} = 0.241 \nonumber\]
To calculate the standard deviation for the analyte’s concentration we must determine the values for \(\overline{S}_{std}\) and for \(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\). The former is just the average signal for the calibration standards, which, using the data in Table \(\PageIndex{1}\), is 30.385. Calculating \(\sum_{i = 1}^{2} (C_{std_i} - \overline{C}_{std})^2\) looks formidable, but we can simplify its calculation by recognizing that this sum-of-squares is the numerator in a standard deviation equation; thus,
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (s_{C_{std}})^2 \times (n - 1) \nonumber\]
where \(s_{C_{std}}\) is the standard deviation for the concentration of analyte in the calibration standards. Using the data in Table \(\PageIndex{1}\) we find that \(s_{C_{std}}\) is 0.1871 and
\[\sum_{i = 1}^{n} (C_{std_i} - \overline{C}_{std})^2 = (0.1872)^2 \times (6 - 1) = 0.175 \nonumber\]
Substituting known values into Equation \ref{5.12} gives
\[s_{C_A} = \frac {0.4035} {120.706} \sqrt{\frac {1} {3} + \frac {1} {6} + \frac {(29.33 - 30.385)^2} {(120.706)^2 \times 0.175}} = 0.0024 \nonumber\]
Finally, the 95% confidence interval for 4 degrees of freedom is
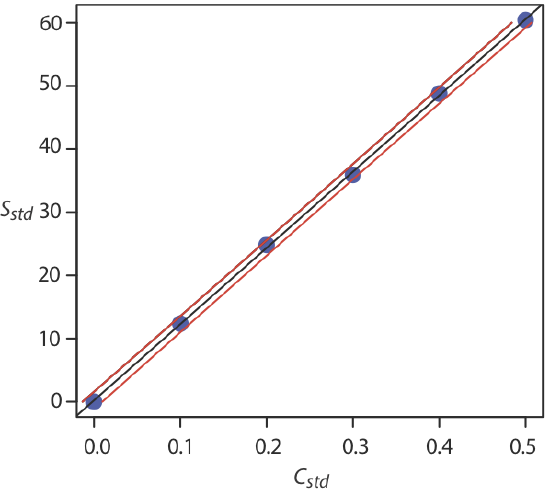
\[\mu_{C_A} = C_A \pm ts_{C_A} = 0.241 \pm (2.78 \times 0.0024) = 0.241 \pm 0.007 \nonumber\]
Figure \(\PageIndex{5}\) shows the calibration curve with curves showing the 95% confidence interval for CA.
In a standard addition we determine the analyte’s concentration by extrapolating the calibration curve to the x-intercept. In this case the value of CA is
\[C_A = x\text{-intercept} = \frac {-b_0} {b_1} \nonumber\]
and the standard deviation in CA is
\[s_{C_A} = \frac {s_r} {b_1} \sqrt{\frac {1} {n} + \frac {(\overline{S}_{std})^2} {(b_1)^2 \sum_{i = 1}^{n}(C_{std_i} - \overline{C}_{std})^2}} \nonumber\]
where n is the number of standard additions (including the sample with no added standard), and \(\overline{S}_{std}\) is the average signal for the n standards. Because we determine the analyte’s concentration by extrapolation, rather than by interpolation, \(s_{C_A}\) for the method of standard additions generally is larger than for a normal calibration curve.
Figure \(\PageIndex{2}\) shows a normal calibration curve for the quantitative analysis of Cu2+. The data for the calibration curve are shown here.
| [Cu2+] (M) | Absorbance |
|---|---|
| 0 | 0 |
| \(1.55 \times 10^{-3}\) | 0.050 |
| \(3.16 \times 10^{-3}\) | 0.093 |
| \(4.74 \times 10^{-3}\) | 0.143 |
| \(6.34 \times 10^{-3}\) | 0.188 |
| \(7.92 \times 10^{-3}\) | 0.236 |
Complete a linear regression analysis for this calibration data, reporting the calibration equation and the 95% confidence interval for the slope and the y-intercept. If three replicate samples give an Ssamp of 0.114, what is the concentration of analyte in the sample and its 95% confidence interval?
- Answer
-
We begin by setting up a table to help us organize the calculation
\(x_i\) \(y_i\) \(x_i y_i\) \(x_i^2\) 0.000 0.000 0.000 0.000 \(1.55 \times 10^{-3}\) 0.050 \(7.750 \times 10^{-5}\) \(2.403 \times 10^{-6}\) \(3.16 \times 10^{-3}\) 0.093 \(2.939 \times 10^{-4}\) \(9.986 \times 10^{-6}\) \(4.74 \times 10^{-3}\) 0.143 \(6.778 \times 10^{-4}\) \(2.247 \times 10^{-5}\) \(6.34 \times 10^{-3}\) 0.188 \(1.192 \times 10^{-3}\) \(4.020 \times 10^{-5}\) \(7.92 \times 10^{-3}\) 0.236 \(1.869 \times 10^{-3}\) \(6.273 \times 10^{-5}\) Adding the values in each column gives
\[\sum_{i = 1}^{n} x_i = 2.371 \times 10^{-2} \quad \sum_{i = 1}^{n} y_i = 0.710 \quad \sum_{i = 1}^{n} x_i y_i = 4.110 \times 10^{-3} \quad \sum_{i = 1}^{n} x_i^2 = 1.378 \times 10^{-4} \nonumber\]
When we substitute these values into Equation \ref{5.4} and Equation \ref{5.5}, we find that the slope and the y-intercept are
\[b_1 = \frac {6 \times (4.110 \times 10^{-3}) - (2.371 \times 10^{-2}) \times 0.710} {6 \times (1.378 \times 10^{-4}) - (2.371 \times 10^{-2})^2} = 29.57 \nonumber\]
\[b_0 = \frac {0.710 - 29.57 \times (2.371 \times 10^{-2}} {6} = 0.0015 \nonumber\]
and that the regression equation is
\[S_{std} = 29.57 \times C_{std} + 0.0015 \nonumber\]
To calculate the 95% confidence intervals, we first need to determine the standard deviation about the regression. The following table helps us organize the calculation.
\(x_i\) \(y_i\) \(\hat{y}_i\) \((y_i - \hat{y}_i)^2\) 0.000 0.000 0.0015 \(2.250 \times 10^{-6}\) \(1.55 \times 10^{-3}\) 0.050 0.0473 \(7.110 \times 10^{-6}\) \(3.16 \times 10^{-3}\) 0.093 0.0949 \(3.768 \times 10^{-6}\) \(4.74 \times 10^{-3}\) 0.143 0.1417 \(1.791 \times 10^{-6}\) \(6.34 \times 10^{-3}\) 0.188 0.1890 \(9.483 \times 10^{-6}\) \(7.92 \times 10^{-3}\) 0.236 0.2357 \(9.339 \times 10^{-6}\) Adding together the data in the last column gives the numerator of Equation \ref{5.6} as \(1.596 \times 10^{-5}\). The standard deviation about the regression, therefore, is
\[s_r = \sqrt{\frac {1.596 \times 10^{-5}} {6 - 2}} = 1.997 \times 10^{-3} \nonumber\]
Next, we need to calculate the standard deviations for the slope and the y-intercept using Equation \ref{5.7} and Equation \ref{5.8}.
\[s_{b_1} = \sqrt{\frac {6 \times (1.997 \times 10^{-3})^2} {6 \times (1.378 \times 10^{-4}) - (2.371 \times 10^{-2})^2}} = 0.3007 \nonumber\]
\[s_{b_0} = \sqrt{\frac {(1.997 \times 10^{-3})^2 \times (1.378 \times 10^{-4})} {6 \times (1.378 \times 10^{-4}) - (2.371 \times 10^{-2})^2}} = 1.441 \times 10^{-3} \nonumber\]
and use them to calculate the 95% confidence intervals for the slope and the y-intercept
\[\beta_1 = b_1 \pm ts_{b_1} = 29.57 \pm (2.78 \times 0.3007) = 29.57 \text{ M}^{-1} \pm 0.84 \text{ M}^{-1} \nonumber\]
\[\beta_0 = b_0 \pm ts_{b_0} = 0.0015 \pm (2.78 \times 1.441 \times 10^{-3}) = 0.0015 \pm 0.0040 \nonumber\]
With an average Ssamp of 0.114, the concentration of analyte, CA, is
\[C_A = \frac {S_{samp} - b_0} {b_1} = \frac {0.114 - 0.0015} {29.57 \text{ M}^{-1}} = 3.80 \times 10^{-3} \text{ M} \nonumber\]
The standard deviation in CA is
\[s_{C_A} = \frac {1.997 \times 10^{-3}} {29.57} \sqrt{\frac {1} {3} + \frac {1} {6} + \frac {(0.114 - 0.1183)^2} {(29.57)^2 \times (4.408 \times 10^{-5})}} = 4.778 \times 10^{-5} \nonumber\]
and the 95% confidence interval is
\[\mu = C_A \pm t s_{C_A} = 3.80 \times 10^{-3} \pm \{2.78 \times (4.778 \times 10^{-5})\} \nonumber\]
\[\mu = 3.80 \times 10^{-3} \text{ M} \pm 0.13 \times 10^{-3} \text{ M} \nonumber\]
Evaluating a Linear Regression Model
You should never accept the result of a linear regression analysis without evaluating the validity of the model. Perhaps the simplest way to evaluate a regression analysis is to examine the residual errors. As we saw earlier, the residual error for a single calibration standard, ri, is
\[r_i = (y_i - \hat{y}_i) \nonumber\]
If the regression model is valid, then the residual errors should be distributed randomly about an average residual error of zero, with no apparent trend toward either smaller or larger residual errors (Figure \(\PageIndex{6}\)a). Trends such as those in Figure \(\PageIndex{6}\)b and Figure \(\PageIndex{6}\)c provide evidence that at least one of the model’s assumptions is incorrect. For example, a trend toward larger residual errors at higher concentrations, Figure \(\PageIndex{6}\)b, suggests that the indeterminate errors affecting the signal are not independent of the analyte’s concentration. In Figure \(\PageIndex{6}\)c, the residual errors are not random, which suggests we cannot model the data using a straight-line relationship. Regression methods for the latter two cases are discussed in the following sections.
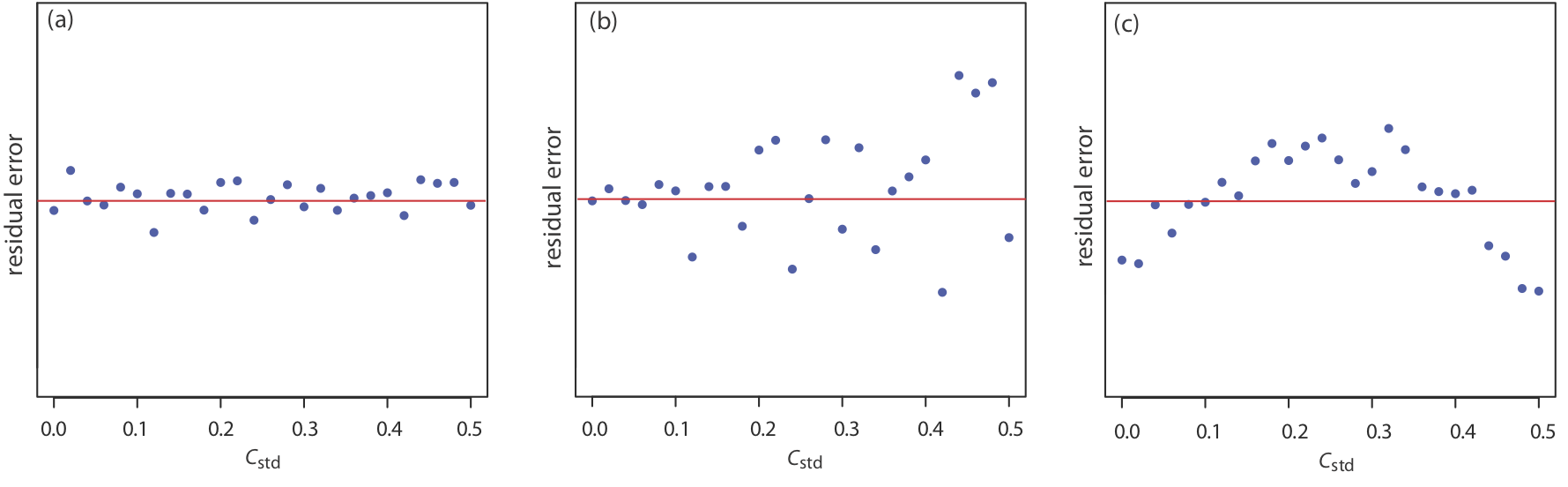
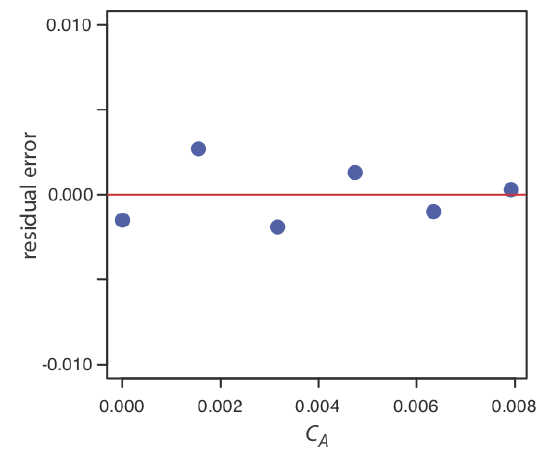
Using your results from Exercise \(\PageIndex{1}\), construct a residual plot and explain its significance.
- Answer
-
To create a residual plot, we need to calculate the residual error for each standard. The following table contains the relevant information.
\(x_i\) \(y_i\) \(\hat{y}_i\) \(y_i - \hat{y}_i\) 0.000 0.000 0.0015 –0.0015 \(1.55 \times 10^{-3}\) 0.050 0.0473 0.0027 \(3.16 \times 10^{-3}\) 0.093 0.0949 –0.0019 \(4.74 \times 10^{-3}\) 0.143 0.1417 0.0013 \(6.34 \times 10^{-3}\) 0.188 0.1890 –0.0010 \(7.92 \times 10^{-3}\) 0.236 0.2357 0.0003 The figure below shows a plot of the resulting residual errors. The residual errors appear random, although they do alternate in sign, and that do not show any significant dependence on the analyte’s concentration. Taken together, these observations suggest that our regression model is appropriate.
Weighted Linear Regression with Errors in y
Our treatment of linear regression to this point assumes that indeterminate errors affecting y are independent of the value of x. If this assumption is false, as is the case for the data in Figure \(\PageIndex{6}\)b, then we must include the variance for each value of y into our determination of the y-intercept, b0, and the slope, b1; thus
\[b_0 = \frac {\sum_{i = 1}^{n} w_i y_i - b_1 \sum_{i = 1}^{n} w_i x_i} {n} \label{5.13}\]
\[b_1 = \frac {n \sum_{i = 1}^{n} w_i x_i y_i - \sum_{i = 1}^{n} w_i x_i \sum_{i = 1}^{n} w_i y_i} {n \sum_{i =1}^{n} w_i x_i^2 - \left( \sum_{i = 1}^{n} w_i x_i \right)^2} \label{5.14}\]
where wi is a weighting factor that accounts for the variance in yi
\[w_i = \frac {n (s_{y_i})^{-2}} {\sum_{i = 1}^{n} (s_{y_i})^{-2}} \label{5.15}\]
and \(s_{y_i}\) is the standard deviation for yi. In a weighted linear regression, each xy-pair’s contribution to the regression line is inversely proportional to the precision of yi; that is, the more precise the value of y, the greater its contribution to the regression.
Shown here are data for an external standardization in which sstd is the standard deviation for three replicate determination of the signal. This is the same data used in Example \(\PageIndex{1}\) with additional information about the standard deviations in the signal.
| \(C_{std}\) (arbitrary units) | \(S_{std}\) (arbitrary units) | \(s_{std}\) |
|---|---|---|
| 0.000 | 0.00 | 0.02 |
| 0.100 | 12.36 | 0.02 |
| 0.200 | 24.83 | 0.07 |
| 0.300 | 35.91 | 0.13 |
| 0.400 | 48.79 | 0.22 |
| 0.500 | 60.42 | 0.33 |
Determine the calibration curve’s equation using a weighted linear regression. As you work through this example, remember that x corresponds to Cstd, and that y corresponds to Sstd.
Solution
We begin by setting up a table to aid in calculating the weighting factors.
| \(C_{std}\) (arbitrary units) | \(S_{std}\) (arbitrary units) | \(s_{std}\) | \((s_{y_i})^{-2}\) | \(w_i\) |
|---|---|---|---|---|
| 0.000 | 0.00 | 0.02 | 2500.00 | 2.8339 |
| 0.100 | 12.36 | 0.02 | 250.00 | 2.8339 |
| 0.200 | 24.83 | 0.07 | 204.08 | 0.2313 |
| 0.300 | 35.91 | 0.13 | 59.17 | 0.0671 |
| 0.400 | 48.79 | 0.22 | 20.66 | 0.0234 |
| 0.500 | 60.42 | 0.33 | 9.18 | 0.0104 |
Adding together the values in the fourth column gives
\[\sum_{i = 1}^{n} (s_{y_i})^{-2} \nonumber\]
which we use to calculate the individual weights in the last column. As a check on your calculations, the sum of the individual weights must equal the number of calibration standards, n. The sum of the entries in the last column is 6.0000, so all is well. After we calculate the individual weights, we use a second table to aid in calculating the four summation terms in Equation \ref{5.13} and Equation \ref{5.14}.
| \(x_i\) | \(y_i\) | \(w_i\) | \(w_i x_i\) | \(w_i y_i\) | \(w_i x_i^2\) | \(w_i x_i y_i\) |
|---|---|---|---|---|---|---|
| 0.000 | 0.00 | 2.8339 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.100 | 12.36 | 2.8339 | 0.2834 | 35.0270 | 0.0283 | 3.5027 |
| 0.200 | 24.83 | 0.2313 | 0.0463 | 5.7432 | 0.0093 | 1.1486 |
| 0.300 | 35.91 | 0.0671 | 0.0201 | 2.4096 | 0.0060 | 0.7229 |
| 0.400 | 48.79 | 0.0234 | 0.0094 | 1.1417 | 0.0037 | 0.4567 |
| 0.500 | 60.42 | 0.0104 | 0.0052 | 0.6284 | 0.0026 | 0.3142 |
Adding the values in the last four columns gives
\[\sum_{i = 1}^{n} w_i x_i = 0.3644 \quad \sum_{i = 1}^{n} w_i y_i = 44.9499 \quad \sum_{i = 1}^{n} w_i x_i^2 = 0.0499 \quad \sum_{i = 1}^{n} w_i x_i y_i = 6.1451 \nonumber\]
Substituting these values into the Equation \ref{5.13} and Equation \ref{5.14} gives the estimated slope and estimated y-intercept as
\[b_1 = \frac {(6 \times 6.1451) - (0.3644 \times 44.9499)} {(6 \times 0.0499) - (0.3644)^2} = 122.985 \nonumber\]
\[b_0 = \frac{44.9499 - (122.985 \times 0.3644)} {6} = 0.0224 \nonumber\]
The calibration equation is
\[S_{std} = 122.98 \times C_{std} + 0.2 \nonumber\]
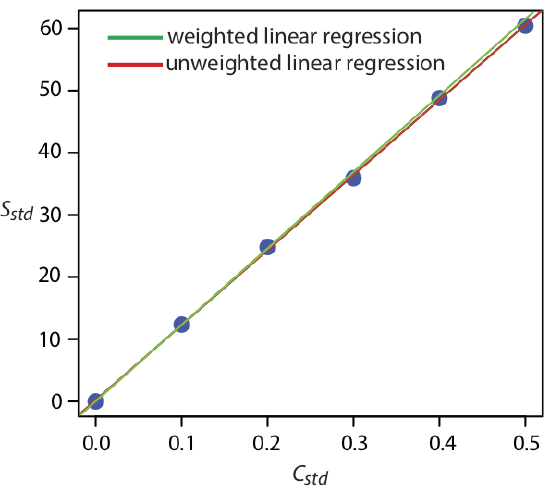
Figure \(\PageIndex{7}\) shows the calibration curve for the weighted regression and the calibration curve for the unweighted regression in Example \(\PageIndex{1}\). Although the two calibration curves are very similar, there are slight differences in the slope and in the y-intercept. Most notably, the y-intercept for the weighted linear regression is closer to the expected value of zero. Because the standard deviation for the signal, Sstd, is smaller for smaller concentrations of analyte, Cstd, a weighted linear regression gives more emphasis to these standards, allowing for a better estimate of the y-intercept.
Equations for calculating confidence intervals for the slope, the y-intercept, and the concentration of analyte when using a weighted linear regression are not as easy to define as for an unweighted linear regression [Bonate, P. J. Anal. Chem. 1993, 65, 1367–1372]. The confidence interval for the analyte’s concentration, however, is at its optimum value when the analyte’s signal is near the weighted centroid, yc , of the calibration curve.
\[y_c = \frac {1} {n} \sum_{i = 1}^{n} w_i x_i \nonumber\]
Weighted Linear Regression with Errors in Both x and y
If we remove our assumption that indeterminate errors affecting a calibration curve are present only in the signal (y), then we also must factor into the regression model the indeterminate errors that affect the analyte’s concentration in the calibration standards (x). The solution for the resulting regression line is computationally more involved than that for either the unweighted or weighted regression lines. Although we will not consider the details in this textbook, you should be aware that neglecting the presence of indeterminate errors in x can bias the results of a linear regression.
See, for example, Analytical Methods Committee, “Fitting a linear functional relationship to data with error on both variable,” AMC Technical Brief, March, 2002), as well as this chapter’s Additional Resources.
Curvilinear and Multivariate Regression
A straight-line regression model, despite its apparent complexity, is the simplest functional relationship between two variables. What do we do if our calibration curve is curvilinear—that is, if it is a curved-line instead of a straight-line? One approach is to try transforming the data into a straight-line. Logarithms, exponentials, reciprocals, square roots, and trigonometric functions have been used in this way. A plot of log(y) versus x is a typical example. Such transformations are not without complications, of which the most obvious is that data with a uniform variance in y will not maintain that uniform variance after it is transformed.
It is worth noting that the term “linear” does not mean a straight-line. A linear function may contain more than one additive term, but each such term has one and only one adjustable multiplicative parameter. The function
\[y = ax + bx^2 \nonumber\]
is an example of a linear function because the terms x and x2 each include a single multiplicative parameter, a and b, respectively. The function
\[y = x^b \nonumber\]
is nonlinear because b is not a multiplicative parameter; it is, instead, a power. This is why you can use linear regression to fit a polynomial equation to your data.
Sometimes it is possible to transform a nonlinear function into a linear function. For example, taking the log of both sides of the nonlinear function above gives a linear function.
\[\log(y) = b \log(x) \nonumber\]
Another approach to developing a linear regression model is to fit a polynomial equation to the data, such as \(y = a + b x + c x^2\). You can use linear regression to calculate the parameters a, b, and c, although the equations are different than those for the linear regression of a straight-line. If you cannot fit your data using a single polynomial equation, it may be possible to fit separate polynomial equations to short segments of the calibration curve. The result is a single continuous calibration curve known as a spline function.
For details about curvilinear regression, see (a) Sharaf, M. A.; Illman, D. L.; Kowalski, B. R. Chemometrics, Wiley-Interscience: New York, 1986; (b) Deming, S. N.; Morgan, S. L. Experimental Design: A Chemometric Approach, Elsevier: Amsterdam, 1987.
The regression models in this chapter apply only to functions that contain a single independent variable, such as a signal that depends upon the analyte’s concentration. In the presence of an interferent, however, the signal may depend on the concentrations of both the analyte and the interferent
\[S = k_A C_A + k_I CI + S_{reag} \nonumber\]
where kI is the interferent’s sensitivity and CI is the interferent’s concentration. Multivariate calibration curves are prepared using standards that contain known amounts of both the analyte and the interferent, and modeled using multivariate regression.
See Beebe, K. R.; Kowalski, B. R. Anal. Chem. 1987, 59, 1007A–1017A. for additional details, and check out this chapter’s Additional Resources for more information about linear regression with errors in both variables, curvilinear regression, and multivariate regression.


