Quadrupolar Coupling
- Page ID
- 1827
Nuclei with spin \(I > \dfrac{1}{2}\) comprise more that 2/3 of the NMR active nuclei. These nuclei exhibit a quadrupolar moment which couples to the electric field gradient resulting in extensive peak broadening. This page is dedicated to understanding the origins of the quadrupole moment and the effects on the NMR line shape. It will be developed through a heavy mathematical treatment, however, the illustrations and captions will provide a pictorial representation of the mathematical treatment.
The Quadrupole Moment
Understanding a Quadrupole
To fully understand the quadrupole interaction we must first establish what a quadrupole is. Quite simply, a quadrupole can be thought of as two dipoles. Unlike a dipole however, the quadrupole will not couple to a symmetric field as the forces and subsequent torques on the quarupole will cancel.
A Quadrupole
If there is an non-symmetric field there will be a force on the quadrupole, i.e., an electric field gradient. We can then define the quadrupole moment as the tendency of the quadrupole to rotate about an axis. Due to the 3D nature of a quadrupole it may be described by a second rank tensor Q where
\[Q=\begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xz} \\ Q_{yx} & Q_{yy} & Q_{yz} \\ Q_{zx} & Q_{zy} & Q_{zz} \end{bmatrix}\]
The quadrupole can then couple to an Electric Field Gradient (EFG) The electric field gradient is denoted a V and is also described by a second rank tensor.
\[V=\begin{bmatrix} V_{xx} & V_{xy} & V_{xz} \\ V_{yx} & V_{yy} & V_{yz} \\ V_{zx} & V_{zy} & V_{zz} \end{bmatrix}\]
EFGs are generated in solids and liquids by th electrons in the sample.
Quadrupolar Nuclei
Within the nucleus of an atom, the protons, and subsequent charge of the nucleus, can be distributed symmetrically or asymmetrically. If the charge distribution is symmetric, the spin,I, of the nucleus is 1/2 and the interaction of the nucleus with electric field gradients is direction independent. However, if the charge distribution is asymmetric I>1/2, and the electric field gradient can interact with the nucleus and exhibit a torque on the nucleus. These nuclei are known as quadrupolar nuclei. It is worth mentioning that the electric field gradient is generated by the electrons present in the sample. Consequently, these nuclei exhibit a quadrupole moment, Q.

While calculations of the quadrupole moment for a given nuclei are beyond the scope of this page, the moments for the nuclei have been calculated and a few examples are listed below.
| Nucleus | Spin | Q (barns) X 103 |
|---|---|---|
| 2H | 1 | 2.86 |
| 6Li | 1 | 0.83 |
| 7Li | 3/2 | -40.6 |
| 10B | 3 | 84.7 |
| 17O | 5/2 | -25.7 |
| 87Rb | 3/2 | 127.1 |
Q can be considered a friction coefficient between rotations of the electric field of the molecule. The larger the Q value, the more strongly the asymmetric nucleus will interact with a non-uniform electric field gradient. This leads to a nuclear spin reorientation in the nucleus. The exception is cubic symmetry (Td or Oh) where the electric field gradient is symmetic resulting in no net effect on the non-spherical nucleus.
Spin Energy Levels
As the spin of a quadrupole nucleus is larger than I=1/2 we develop multiple energy levels (2I+1) and therefore multiple transitions are expected. In half-integer spin systems (e.g. 3/2, 5/2, 7/2) There is still a -1/2 to 1/2 transition knowns as the central transition. The other transitions are known as satellite transitions. A good example is listed below:
Boron-11 (11B) is a classic example of the spectral changes caused by the quadrupole moment. With a nuclear spin of I =\(\frac{3}{2}\) and Δm = ±1 transitions being allowed, 4 states are produced: m = \(\frac{3}{2}\),\(\frac{1}{2}\), -\(\frac{1}{2}\), -\(\frac{3}{2}\). However, only 3 transitions are possible:
\[\dfrac{3}{2}\leftrightarrow\dfrac{1}{2}\,\] Satellite Transition
\[ \dfrac{1}{2}\leftrightarrow-\dfrac{1}{2}\] Central Transition
\[ -\dfrac{1}{2}\leftrightarrow-\dfrac{3}{2}\] Satellite Transition
While it may be expected that these transitions happen at the same energy levels, we we see in a latter section that this is not the case!
Derivation of the Hamiltonian
If we consider the picture below, We can describe the electrostatic interaction between the electron, which has a non-spherical charge distribution, and the protons of the nucleus through a coulombic interaction such that
\[U=-\sum_{p=1}^Z \dfrac{e^2}{| \vec{r_p} -\vec{r_e}|}\]
where Z is the atomic number, and rp and re are the proton and electron distances.
(insert picture)
Most likely, the PAS of the rp and re will not coincide with the lab frame and instead should be expressed by the principle axis system of angles \( \theta_p , \phi_p, \theta_e\) as denoted in the figure above. Converting the reference frame to a frame with its origin at the center of the nucleus we can obtain
\[\dfrac{1}{| \vec{r_p} -\vec{r_e}|} = 4 \pi \sum_{l=0}^{\infty} \sum_{m=-l}^l \dfrac{1}{2l+1} \dfrac{r_<^l}{r_>^{l+1}} Y_m^{(l)*}(\theta_p, \phi_p)Y_m^{(l)}(\theta_e, \phi_e)\]
where r< is the smaller value between rp or re and r> is the larger value, and Y denotes the spherical harmonics. In the case that the electrons do not penetrate the nucleus, re>rp and
\[U=-4 \pi e^2 \sum_{p=1}^Z \sum_{l=0}^{\infty} \sum_{m=-l}^l \dfrac{1}{2l+1} \dfrac{r_p^l}{r_e{l+1}} Y_m^{(p)*}(\theta_p, \phi_p) Y_m^{(p}(\theta_e, \phi_e)\]
From thie above equation, we will derive the Hamiltonian for the quadrupolar interaction, HQ. In order to do this we first start by showing the symmetry relation
\[Y_m^{(l)}=(-1)^mY_{-m}^{(l)}*\]
Then,
\[\sum_{m=-l}^{l}Y_m^{(l)*}(\theta_p, \phi_p)Y_m^{(l)}(\theta_e, \phi_e)=\sum_{m=-l}^{l}(-1)^m Y_{-m}^{(l)*}(\theta_p, \phi_p)Y_m^{(l)}(\theta_e, \phi_e)=Y^{(l)}(\theta_p, \phi_p) \cdot Y^{(l)}(\theta_e, \phi_e)\]
The dot product infers that we can then separate the potential energy equation into two pieces, one for the nuclear energy denoted as Q(l) and one for the electronic energy as k(l). These expressions are given as
\[Q^{(l)}=e\sum_{p=1}^Z \sqrt{\dfrac{4\pi}{2l+1}} r_p^l Y^{(l)}(\theta_p, \phi_p)\]
\[k^{(l)}=-e\sqrt{\dfrac{4\pi}{2l+1}} \dfrac{1}{r_e^{l+1}} Y^{(l)}(\theta_p, \phi_p)\]
The total potential energy is then
\[U=\sum_l Q^{(l)} \cdot k^{(l)}\]
for l=0
\[U=-\dfrac{Ze^2}{r_e}\]
which is the expected coulombic interaction between the electron and the nucleus. The next higher order (l=1) corresponds to the interaction between a nucleus electric dipole moment and the electric field generated by the electrons. Since rp is an odd operator, the expectation value of Q is zero andthe potential energy, U, is also zero. The next higher interaction is l=2 corresponding to electric quadrupole interaction.
\[H_Q=U^{(2)}=Q^{(2)} \cdot k^{(2)}\]
In order to fully expand this Hamiltonian, we want to relate Q and K to the molecular parameters. Q will be related to only the operators involving the nuclear spin such that
\[Q^{(2)}=AT^{(2)}\]
where T is the spherical tensor. K will be related to the EFG. Lets begin our discussion by expanding Q. Consider the effect of Q on the spins such that
\[\langle I, m_{I=I} | Q_0^{(2)}|I, m_{I=I} \rangle =e\sqrt{\dfrac{4 \pi}{5}} \sum_p r_p^2 \langle I, I| Y_0^{(2)}(\theta_p, \phi_p)|I, I\rangle\]
\[= \dfrac{1}{2} e \langle I,I| \sum_p (3z_p^2-r_p^2)|I,I\rangle\]
In which \(sum_p (3z_p^2-r_p^2)\) is the quadrupolar moment. Therefore this term reduces to
\[=\dfrac{1}{2}eQ\]
Using the irreducible tensors,
\[=A\langle I,I|T_0^{(2)}|I,I\rangle\]
\[=A\langle I,I|\dfrac{1}{\sqrt{6}}(3I_0^2-I^2)|I,I\rangle\]
\[=\dfrac{A}{\sqrt{6}}(3I^2-I(I+1))\]
\[=\dfrac{A}{\sqrt{6}}I(2I+1)\]
We can then solve for A
\[A=\sqrt{\dfrac{3}{2}} \dfrac{eQ}{I(2I-1)}\]
which yeilds
\[Q^{(2)}=\sqrt{\dfrac{3}{2}}\dfrac{eQ}{I(2I-1)}T^{(2)}\]
Adopting a similar approach for k
\[\dfrac{d^2}{dr_i dr_j}(\dfrac{-e}{p})=-e\dfrac{3r_ir_j-r^2 \delta_{ij}}{r^5}=V_{r_ir_j}\]
Then
\[k_0^2=-e\sqrt{\dfrac{4 \pi}{5}} \dfrac{1}{r_e^3} Y_0^{(2)}(\theta_p, \phi_p)\]
\[=\dfrac{-e}{2}\dfrac{3Z_e^2-r_e^2}{r_e^5}\]
\[\dfrac{1}{2}V_{zz}\]
We can expand k(2) and find
\[k_{\pm 1}^{(2)}=\mp \dfrac{1}{2} \sqrt{\dfrac{2}{3}}(V_{zx} \pm iV_{yz})\]
\[k_{\pm 2}^{(2)}=dfrac{1}{4} \sqrt{\dfrac{2}{3}}(V_{xx}-V_{yy} \pm 2iV_{xy})\]
Substituting the equations in for k and Q we would be able to obtain HQ in an arbitary frame. However, it is much more convient to express HQ in terms of the principle axis system of the EFG. Therefore, we choose the following condition
\[V_{i,j}=0\]
unless i=j. Resulting in
\[k_{\pm 1}^{(2)}=0\]
and we obtain our expression for the HQ as
\[H_Q=\dfrac{eQ}{I(2I-1)}[\dfrac{1}{4}I_{+1}^2(V_{xx}-V_{yy})+\dfrac{1}{4}(3I_0^2-I^2)V_{zz}+\dfrac{1}{4}I_{-1}^2 (V_{xx}-V_{yy})\]
\[=\dfrac{eQ}{4I(2I-1)}[(3I_0^2-I^2)V_{zz}+(I_{+1}^2+I_{-1}^2) (V_{xx}-V_{yy})\]
We can further simplify this expression by converting the electronic operators (Vij) by defining
\[V_{zz}=eq\]
and
\[V_{xx}-V_{yy}=\eta eq\]
Yielding
\[H_Q=\dfrac{e^2Q}{4I(2I-1)}[(3I_0^2-I^2)+(I_{+1}^2+I_{-1}^2) \eta\]
Furthermore,
\[I_{+1}^2+I_{-1}^2=I_x^2-I_y^2\]
and
\[I^2=I_x^2+I_y^2+I_z^2\]
Then
\[H_Q^{PAS}=\dfrac{e^2Q}{4I(2I-1)}[2I_z^2-I_x^2-I_y^2+\eta(I_x^2-I_y^2)]\]
\[=\dfrac{e^2Q}{4I(2I-1)}(I_x,I_y,I_z)\begin{bmatrix} \eta-1 &0&0 \\ 0&-\eta-1&0 \\ 0&0&2 \end{bmatrix} \begin{pmatrix} I_x\\I_y\\I_z \end{pmatrix}\]
Then HQ reduces to
\[H_Q^{PAS}=\dfrac{e^2Q}{4I(2I-1)}\vec{I} \cdot Q \cdot \vec{I}\]
Expansion of the Hamiltonian
Classical Expansion
For those who wish to not delve into the complex treatment of the quadrupolar hamiltonian we can treat the Hamiltonian semi-classically and derive an expression for the quadrupolar Hamiltonian. The interaction of a quadrupole with a field gradient in an arbitrary frame (The PAS of the of the electric field gradient) may be described by
\[\hat{H}_{Q}=\dfrac{eQ}{2I(2I-1)\hbar} \hat{I} \cdot V \cdot \hat{I}\]
We can actually re-write this expression to account for the description of the EFG that was given in the Cartesian components if we change spin operators to their Cartesian analogues. This gives the result
\[\hat{H}_{Q}=\dfrac{eQ}{6I(2I-1)\hbar} \sum_{\alpha, \beta = x, y, z} V_{\alpha \beta} [\frac{3}{2} (\hat {I}_\alpha \hat {I}_\beta + \hat {I}_\beta \hat {I}_\alpha)- \delta_{\alpha \beta} \hat{I}^2]\]
The EFG is traceless and can be described using an asymmetry parameter define as
\[\eta_Q= \dfrac{V_{xx}^{PAS}-V_{yy}^{PAS}} {V_{zz}^{PAS}}\]
and the magnitude of the EFG will then be given as
\[eq=V_{zz}^{PAS}\]
We must at this point recognize that we are in the reference frame of the electric field gradient. The HQ in the reference frame of the EFG is then
\[\hat{H}_{Q}=\dfrac{e^2Qq}{4I(2I-1)\hbar} \left [3\hat{I}_{zz}^{2 PAS}-\hat{I^2}+\eta(\hat{I}_{xx}^{2 PAS}-\hat{I}_{yy}^{2 PAS}) \right]\]
For the remainder of the discussions we can simplify the constant term to \(\chi\),
\[\chi=\frac{e^2qQ}{\hbar}\]
This is known as the quadrupole coupling constant and is the accpeted term in the NMR literature. Readers must be wary however as there are several different definitions floating in the literature. The expansion of the Hamiltonian is done using perturbation theory. It has been shown that experimental spectra may be exactly calculated using the first and second perturbations to the Hamiltonian. Using this information, the Hamiltonian may be expanded in terms of polar coordinates and raising and lowering operators. This is done to transform the Hamiltonian from the PAS of the EFG into the laboratory frame
\[\hat{H}_Q=\dfrac{\chi}{4I(2I-1)} \dfrac{1}{2}(3\cos^2 \theta-1)(3 \hat{I}_z^2- \hat{I}^2)\]
\[+\dfrac{3}{2}\sin\theta \cos\theta \left[\hat{I}_z(\hat{I}_++\hat{I}_-)+(\hat{I}_++\hat{I}_-)\hat{I}_z\right]\]
\[+\dfrac{3}{4} \sin^2 \theta (\hat{I}_+^2+\hat{I}_-^2)\]
\[+\eta_{Q}\dfrac{2\pi \chi}{4I(2I-1)h}[ \dfrac{1}{2} \cos2\phi [(1-\cos^2 \theta)(3\hat{I}_z^2- \hat{I}^2)\]
\[+(\cos^2 \theta+1)(\hat{I}_+^2+\hat{I}_-^2)]\]
\[+\dfrac{1}{2} \sin \theta [\cos \theta \cos2 \phi -i\sin2 \phi)(\hat{I}_+\hat{I}_z+\hat{I}_z\hat{I}_+)\]
\[+(\cos \theta \cos2 \phi+\sin2 \phi)(\hat{I}_-\hat{I}_z+\hat{I}_z\hat{I}_-)]\]
\[+(i/4)\sin2 \phi \cos \theta(\hat{I}_+^2-\hat{I}_-^2)\].
From which we can get first and second order corrections to the energy levels,
\[E_m^{(1)}=\dfrac{\chi}{4I(2I-1)}(I(I+1)-3m^2) \left[\dfrac{1}{2}(3\cos^2\theta-1)-\eta \cos2\phi(\cos^2\theta-1) \right]\]
\[E_m^{(2)}=-\dfrac{\chi^2 m}{4I(2I-1) \omega_0} - \dfrac{1}{5} (I(I+1)-3m^2)(3+\eta_Q^2)\]
\[+\dfrac{1}{28}(8I(I+1-12m^2-3)[(\eta_Q^2-3)(3\cos^2 \theta -1)+6\eta_Q\sin^2 \theta \cos2\phi\]
\[+\dfrac{1}{8}(18I(I+1)-34m^2-5)[\dfrac{1}{140}(18+\eta^2)(35\cos^4\theta-30\cos^2\theta+3)\]
\[+\dfrac{3}{7}\eta_Q\sin\theta(7\cos^2\theta-1)\cos2\phi+\dfrac{1}{4}\eta_Q^2\sin^4\theta \cos4\phi]\].
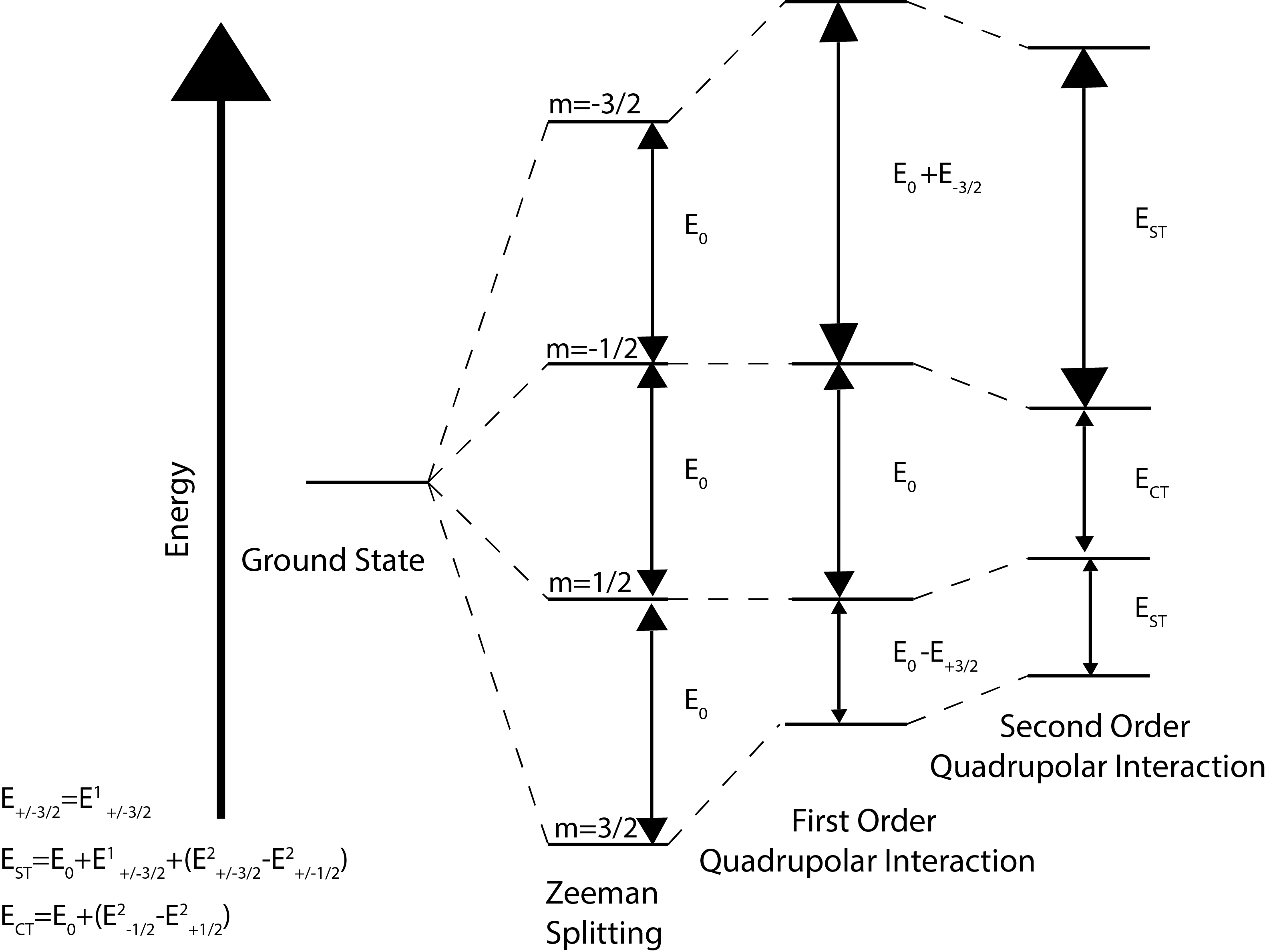
An illustrative figure showing how the energy levels change according to the Zeeman, the first, and the second order quadrupolar interactions is shown below for a spin 3/2 nucleus. Interestingly, he first order approximation does not affect the central transition, while the second order transition is inversely proportional the Larmor frequency. With increasing field, the second order effect on the central transition decreases.
Quadrupolar Lineshapes
The signal exhibited by the quadrupolar nucleus exhibits a very characteristic powder pattern. Looking at the energy levels, it is easy to see there are multiple transitions which can occur. For a spin 1 nucleus, the transitions are from -1 to 0 and 0 to 1. These two transitions manifest themselves as a double horned powder pattern, each horn representative of a transition. The difference in intensities is due to the alignment of the crystallites with respect to the magnetic field. If the crystallite is aligned with the B0 field, then after application of a \(\frac{\pi}{2}\) pulse, it will lie in the x-y plane and consequently contribute fully to the signal. If the crystallite is oriented with some angle relative to the B0 axis and a pulse is applied, it will not process as long and consequently will not be detected for as long and give less of a signal.
The frequency at which the transitions will occur is given by the quadrupolar frequency defined as
\[\omega_Q(\theta)=\omega_0-\dfrac{3}{8} \left(\dfrac{2m-1}{I(2I-1)}\right)\chi (3\cos^2\theta-1)\]
from this it is easy to see why two horns are observed. m is either 1 (red) or -1 (blue) which changes the sign of the quadrupolar perturbation to the Larmor frequency.
For nuclei, such as 87Rb, which have multiple transitions, the powder patterns are more complex. Similar to the CSA the lineshape is dependent on the magnitude of \(\chi\) and \(\eta\), as shown in the figure below.
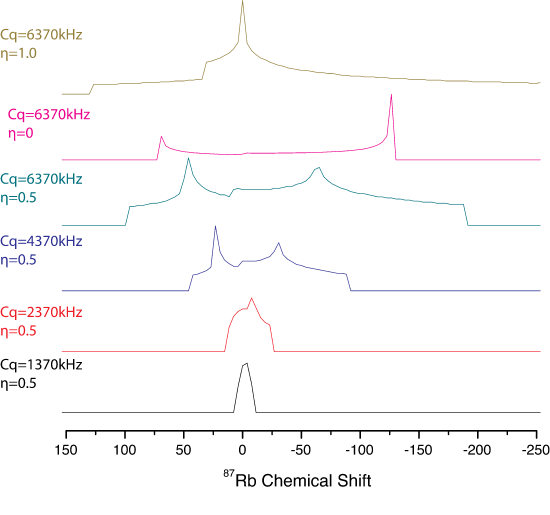
Typically, the satellite transitions are not observed in quadrupolar spectra. The frequency for a symmetric transition, such as -1/2 to 1/2 in quadrupolar nuclei may be represented by the sum of the 0th 2nd and 4th rank Legendre polynomials or mathematically as
\[\nu_{m,-m}=\sum \limits_{l=0,2,4}({\alpha,\beta,\gamma)C_l(I,m)P_l\cos\theta_{MA}}\]
where
\[C_0(I,m)=2m[I(I+1)-3m^2]\]
\[C_2(I,m)=2m[8I(I+1)-12m^2-3]\]
\[C_4(I,m)=2m[18I(I+1)-34m^2-5]\]
\[P_2(\cos\theta)=\dfrac{1}{2}(3\cos^2\theta-1)\]
\[P_4(\cos\theta)=\dfrac{1}{8}(35\cos^4\theta-30\cos^2\theta+3)\]
The second and fourth rank interactions also have associated frequencies. These are given below
\[v_2^Q=\dfrac{1}{192\nu_L}[\dfrac{\chi}{I(2I-1)h}]^2[I(I+1)-\dfrac{3}{4}]F_2(\theta,\phi)\]
\[v_4^Q=\dfrac{1}{3360\nu_L}[\dfrac{\chi}{I(2I-1)h}]^2[I(I+1)-\dfrac{3}{4}]F_4(\theta,\phi)\]
\[F_2(\theta,\phi)=\dfrac{35}{4}(3-\eta_Q\cos2\phi)^2\sin^4\theta-5(18+\eta_Q^2-9\eta_Q\cos2\phi)\sin^2\theta+18+\eta_Q^2\]
\[F_4(\theta,\phi=2(3\eta_Q\cos2\phi-\dfrac{2}{3}\eta_Q^2-3)\sin^2\theta+\dfrac{1}{21}(22\eta_Q^2-90\eta_Q\cos2\phi+120\].
These equations are more useful mathematically and become important in the discussion of pulse sequences of quadrupolar nuclei.
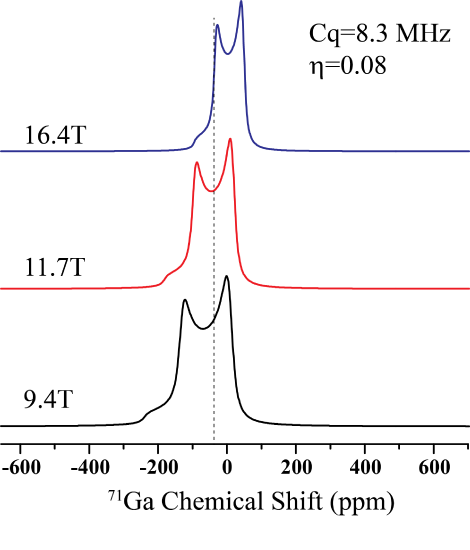
Magnetic Field Effects and the Center of Gravity
The nature of the quadrupolar interaction is heavily influenced by the magnetic field. Below is a figure that shows the field dependence of a Ga resonance in \(\beta\)-Ga2O3. The reader should take note of two things. First, Note how the spectrum narrows as the field is increased. This shows the effect of the central transition is inversely proportional to \(\omega_0\). Second, note the shift in the center of gravity of the peak. As the field increases, the peak shifts progressivley upfield, although the isotropic peak position, denoted by the dotted line is constant.
Quadrupole Moments: Effects in NMR Spectra
As mentioned earlier, a quadrupolar nucleus is efficiently relaxed by a non-uniform electric field that is a product of the solute molecules interaction with the dipolar solvent. This relaxation is dependent on the interaction of the electric field gradient at the nucleus. When the nucleus is in a molecule that is surrounded by a non-spherical electron density distribution, it creates a gradient. The field gradient, q, describes the electron charge cloud’s deviation from spherical symmetry. The value of q is found to equal zero if the groups around the quadrupolar nucleus have a cubic symmetry, such as in the Td point group. However, if a non-cublic molecule has a threefold or higher symmetry axis, the deviation from spherical symmetry is expressed as a magnitude of q. The two parameters, q, the field gradient, and η, the asymmetric parameter, become necessary only if the molecule's point group's highest symmetry axis is a threefold symmetry or less. Depending on the molecule, certain cancellations can take place leading the asymmetric parameter, η, to equal zero. This is caused by a combination of very specific bond angles and charge distribution in the molecule being analyzed. Ultimately, the effectiveness of the relaxation is dependent on the magnitude of the electric field gradient, q.
Linewidth broadening in the NMR spectrum is consequential of the rapid nuclear quadrupole relaxation of the quadrupole nucleus. Consider an analogous situation: chemical exchange. It is known that when the nuclei’s spin state rapidly changes it causes broadening in the spectrum. Similarly, the nuclear quadrupole relaxation rates of a quadrupolar nucelus corresponds to an intermediate rate of chemical relaxation.The apparent broadening effect also influences the spectra of the other nuclei attached to the quadrupolar nucleus, including protons. In some cases, the rapid nucleur quadrupole relaxation times (T1) can cause extensive homogenous broadening (consequential of readily relaxing nuclei, seen in Figure 2) rendering the proton signal of the quadrupolar nucleus completely unobservable in the 1H NMR spectrum. T1 is determined by two factors: the electric quadrupole moment (Q) and the presence of the electric field gradient (q) across the nucleus.
A common approach to resolving quadrupolar effects on the spectra of solution state NMR is elevating temperatures while collecting NMR data. The molecular reorientational correlation times are then shorter than the normal time scale, so the homogenous broadening of the line can be reduced. Unfortunately, the temperature required to create this motional tapering is unfeasibly high for many samples that would deem this technique necessary.
References
- Smith, J.A.S., Nuclear Quadrupole Resonance Spectroscopy: General Principles. J Chem. Ed. 1971, 48, (1), 39.
- Drago, Russell S. "Quadrupole Moments" Physical Methods for Chemists. Ft. Worth: Saunders College Pub., 1992.
- Pyykkö, P., Spectroscopic Nuclear Quadrupole Moments. Mol. Phys. 2001, 99, (19), 1617.
- Gerothanassis, I.P., Kalodimos, C.G., NMR Shielding and the Periodic Table. J. Chem. Ed. 1996, 73, 801. DOI: 10.1021/ed073p801
- Laidler, K.J., Meiser, J.H., Sanctuary, B.C. "Magnetic Interaction Leading to Spectra Consequences" Physical Chemistry. New York: Houghton Mifflin Company., 2003.
- Harris, R.K., Mann, B.E., NMR and the Periodic Table, Acadademic Press, New York, 1978.
- ie.lbl.gov/toipdf/mometbl.pdf
Contributors and Attributions
- Derrick C. Kaseman (UC Davis) and Megan McKenney (UCDavis)